Министерство образования и науки Российской Федерации

Федеральное государственное бюджетное образовательное учреждение Высшего Профессионального Образования

САМАРСКИЙ ГОСУДАРСТВЕНЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

КУРСОВАЯ РАБОТА

“Исследование одноконтурной системы управления частотной вращения двигателя постоянного тока”

Вариант №7

Выполнил студент :

Никулин М.С.

Руководитель:

Абакумов А.М.

Самара 2013 г.

Содержание

1. Техническое задание 3

2. Описание динамических свойств отдельных элементов САУ в форме передаточных функций и разработка алгометрической схемы системы 4

3. Анализ устойчивости системы с использованием необходимого и достаточного условия устойчивости и алгебраического критерия Гурвица. Определение предельного коэффициента усиления системы 7

4. Исследование характеристик исходной системы в разомкнутом состоянии 10

5. Исследование характеристик исходной системы в замкнутом состоянии……………………………………………………….................16

6. Исследование характеристик замкнутой скорректированной системы с ПИ - регулятором 19

7. Сравнительный анализ показателей качества регулирования 21

8. Используемая литература 22

1 Техническое задание.

Рис. 1

Параметры управляемого преобразователя		Параметры двигателя					Параметры усилителя и датчика О.С.
32	0,0035	1,6	0,03	0,22	0.8	22		1,2	50

2.Описание динамических свойств отдельных элементов сау в форме передаточных функций и разработка алгоритмической схе-мы системы.

Рассмотрим динамические свойства элементов системы [2].

Свойства П – регулятора описываются коэффициентом усиления .

Свойства вентильного преобразователя (ВП) описываются передаточной функцией (ПФ) апериодического звена

,

где ; .

Динамические свойства ДПТ независимого возбуждения по управляющему воздействию описываются ПФ

где U_Я – напряжение на якоре;

; ; .

Приведем передаточную функцию к типовому виду. Проверяем выполнение условия 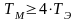. Для рассматриваемого примера оно выполняется. Тогда ПФ можно [2] представить в виде ПФ апериодического звена второго порядка

.

Решая квадратное уравнение

,

находим его корни

;

;

.

И далее вычисляем значения новых постоянных и

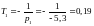с; с.

Для удобства последующего набора модели двигателя представим полученную передаточную функцию в виде двух звеньев

ПФ двигателя по возмущающему воздействию в виде изменения статического тока I_С , пропорционального моменту на валу, отличается только коэффициентом передачи

,

где коэффициент передачи двигателя по возмущению

.

Тахогенератор в системах электропривода рассматривается как пропорциональное звено, и его свойства описываются коэффициентом передачи

С учетом изложенного, алгоритмическая схема системы может быть представлена в виде, показанном на рис. 2.

Рис. 2

3. Анализ устойчивости системы с использованием необходимого и достаточного условия устойчивости и алгебраического критерия Гурвица. Определение предельного коэффициента усиления системы.

1. Предположим, что мы отказались от использования замкнутой системы и сделали ее разомкнутой (для этого достаточно разорвать цепь, по которой сигнал тахогенератора подается на вход регулятора). Исследуем устойчивость разомкнутой системы. Найдем ПФ системы в разомкнутом состоянии. Все звенья системы в разомкнутом состоянии включены последовательно, поэтому передаточная функция будет равна произведению ПФ отдельных звеньев

где коэффициент усиления разомкнутой системы

.

Обозначим знаменатель ПФ разомкнутой системы B(p), приравняем его к нулю

,

и найдем корни характеристического уравнения разомкнутой системы

; ;

.

Согласно необходимому и достаточному условию [1] для устойчивости САУ необходимо, чтобы вещественная часть всех корней характеристического уравнения была меньше нуля. В данном случае все корни вещественные отрицательные, следовательно, разомкнутая система устойчива.

2. Перейдем к исследованию замкнутой САУ. Для исследования устойчивости замкнутой системы с помощью критерия Гурвица найдем ПФ замкнутой системы

.

Характеристическое уравнение замкнутой системы D(p) совпадает со знаменателем полученной ПФ:

.

Раскрыв скобки в выражении для D(p), после преобразований приведем его к виду

,

где с³;

с;

.

Из коэффициентов полученного характеристического уравнения 3-го порядка составляем квадратную матрицу

.

Находим определители

;

Численное значение третьего определителя можно не рассчитывать, т.к. его знак полностью определяется знаком второго определителя

Согласно критерию Гурвица для устойчивости системы необходимо, чтобы коэффициент a₀ и все определители были больше нуля. Поскольку второй и третий определители меньше нуля условия устойчивости не выполняются – замкнутая система неустойчива.

Таким образом, при заданном коэффициенте усиления П-регулятора замкнутая система будет неустойчива.

Найдем далее предельный коэффициент усиления разомкнутой системы . Это коэффициент усиления разомкнутой системы, при котором она находится на границе устойчивости. Очевидно, что при уменьшении второй определитель может стать равным нулю – в этом случае система будет находиться на границе устойчивости, а при дальнейшем уменьшении определитель станет больше 0 – система станет устойчивой. Приравняем второй определитель к нулю

,

и найдем значение предельного коэффициента усиления

.