12. Методологические подходы к построению дискретных моделей
Изменения состава и состояния в дискретных имитационных системах происходит в дискретные моменты времени, называемые событиями. Под событием понимается мгновенное изменение состояния модели, произошедшее в результате осуществления множества взаимодействий между компонентами модели в один и тот же момент имитационного времени.
Взаимосвязь между событиями, действиями и процессами представлена рис
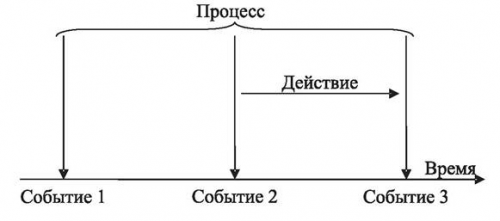
Рис. 4.1. Взаимосвязь между событиями, действиями и процессами
Функционирование дискретной системы можно описать:
определяя изменения состояния системы, происходящие в моменты свершения событий;
описывая действия, в которых принимают участие элементы системы;
описывая процесс, через который проходят элементы.
Процесс – это ориентированная во времени последовательность событий, которая может состоять из нескольких действий.
Эти представления лежат в основе трех альтернативных методологических подходов к построению дискретных имитационных моделей, называемых обычно:
событийный подход;
подход сканирования активностей (на практике получил небольшое распространение);
процессно-ориентированный подход (включает транзактный способ имитации).
Это основные концепции (схемы) структуризации для дискретных имитационных моделей. Их основа закладывается в некоторые языки и системы моделирования. Примерами могут служить языки моделирования:
GASP, SIMSCRIPT, ориентированные на события;
язык работ SLAM;
широко распространенные языки моделирования GPSS, SIMULA и др., предназначенные для описания параллельных процессов.
13. Модели системной динамики
Под непрерывной системой обычно понимается система, состояние которой изменяется непрерывным образом в зависимости от некоторых независимых переменных (обычно времени).
Языки имитационного моделирования непрерывных систем предназначены для моделирования динамических объектов с непрерывным фазовым пространством и непрерывным временем. Как правило, такие объекты описываются с помощью систем дифференциальных (интегро-дифференциальных) уравнений. Однако, в имитационном моделировании формализация явлений в виде математических схем – больше дань традициям, сегодня находят применение подходы, основанные на графической технике структуризации моделируемых динамических процессов.
Классическим примером языков моделирования такого типа явился язык DYNAMO, предложенный Дж. Форрестером. Дж. Форрестер – крупнейший специалист, разработчик концепции системной динамики, основные его работы: “Основы кибернетики предприятия” (1961г.); “Динамика развития города” (1970 г.); “Мировая динамика” (1974 г.) В этих работах изложен метод системной динамики или концепция потокового подхода в имитации, а также исследуются динамика предприятия, урбанизированной территории, проблемы развития человеческой цивилизации на основе предложенной концепции.
Методы и техника построения моделей системной динамики оказали большое влияние на формирование технологии имитационного моделирования. Сейчас появилось много систем моделирования, т.к. iThink, Vensim, Powersim в которых возможности моделирования непрерывных и нелинейных динамических систем дополнены удобными графическими интерфейсами. Сейчас много фирм разрабатывают системы моделирования, реализующие принципы системной динамики, предлагают консалтинговые услуги по моделированию систем на основе инструментальных средств, поддерживающих нормативные подходы методов системной динамики. Существует международное научное общество, которое развивает и совершенствует методы системного анализа и моделирования систем на основе концепции системной динамики.
Модели системной динамики получили широкое распространение в задачах исследования сложных систем из сферы производства и экономики, торговли и городского хозяйства, из области социальных проблем, проблем экологии и охраны окружающей среды. Эти модели были первыми машинными моделями, положившими начало новому направлению в системных исследованиях – так называемому глобальному моделированию, охватывающему проблемы мирового развития – моделирование мировой экономической системы.