Міністерство освіти і науки, молоді та спорту України

Національний університет водного господарства та природокористування

Кафедра автоматизації, електротехнічних та комп’ютерно-інтегрованих технологій

Звіт

по навчальній практиці

з комп’ютерного моделювання

Виконав:

студент 2 курсу

АУТП-22

Кузьмич С.М.

Перевірив:

Гудь В. М.

Рівне 2013

Мета та завдання навчальної практики

Метою практики є набуття знань, умінь та навичок студентів з комп’ютерного моделювання фізичних процесів та електронних пристроїв. Завдання практики полягає у створенні комп’ютерних моделей фізичних процесів і складається із чотирьох завдань, які оформляються в електронному та рукописному вріантах.

Варіант завдання студент визначає самостійно за двома останніми цифрами номера залікової книжки.

Практика розбивається на чотири етапи. Протягом кожного із них студент виконує одне завдання, оформляє його та здає викладачу, котрий керує практикою.

У результаті проходження практики студент повинен

знати: методи комп’ютерного моделювання фізичних процесів та способи представлення моделей.

вміти: створювати математичні та комп’ютерні моделі фізичних процесів. Проводити аналіз процесів фізичних процесів на основі їх математичних моделей.

Завдання 1

Методи розв'язку алгебраїчних та диференціальних рівнянь та їх систем.

1. Знайти корені або формули коренів для обчислення алгебраїчних (приведених в табл. 1) та диференціальних (приведених в табл. 2) рівнянь та їх систем з допомогою засобів середовища MatLab та аналітично.

2. Порівняти результати, отримані аналітично і за допомогою засобів MatLab та зробити відповідні висновки.

1. Нелінійні алгебраїчні рівняння

№	Рівняння
31

_{де а- певний параметр;}

В Matlab:

>> [x]=solve('x^5-a*x^3+2*x^2-2*a')

x =

-a^(1/2)

(-2)^(1/3)

a^(1/2)

- (-2)^(1/3)/2 - ((-2)^(1/3)*3^(1/2)*i)/2

- (-2)^(1/3)/2 + ((-2)^(1/3)*3^(1/2)*i)/2

Остання цифра шифру 1. Електрична ємність системи двох рівнобіжних пластин прямокутної форми (див. малюнок) при a ≥ d і b ≥ d може бути визначена по формулі

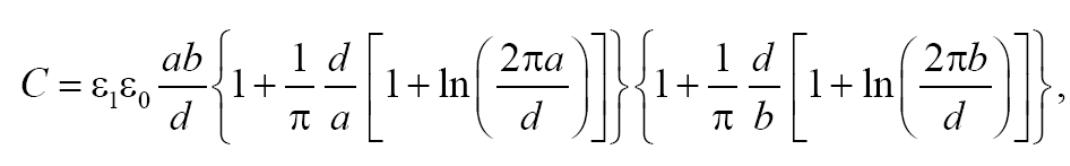
де ε₁ − відносна діелектрична проникність середовища, ε₀ = 8,85⋅10^–12 Ф/м; a и b − раозміри пластин; d − відстань між пластинами, π = 3,14….

Знайдіть зазор d, що забезпечує одержання необхідної ємності C при зазначених у таблиці параметрах.

Параметр	Останні цифри шифру
	01	11	21	31	41	51	61	71	81	91
а, мм	0,002	0,004	0,003	0,020	0,005	0,006	0,008	0,01	0,015	0,012
b, мм	0,005	0,006	0,004	0,008	0,003	0,004	0,01	0,015	0,02	0,01
ε1	4,1	10	3,7	7	9,6	5,1	6	4	3,7	9
С, пФ	10	2	6,5	10	15	9	12	8	5,6	4,7

Matlab>> e0=8.85*10^(-12)

[d]=solve('10=7*8.8500e-012*(0.02*0.008)*(1+(1/pi)*(d/0.02)*(1+ln((2*pi*0.02)/d)))*(1+(1/pi)*(d/0.008)*(1+ln((2*pi*0.008)/d)))')

d =

20820.925651970239626325884321456*i - 92522.906285240588378510747235031

1.3.Системи лінійних рівнянь.

11

а) аналітично (методом Гауса чи Крамера в EXCEL),

Коефіціенти			Вільні члени
1,2	1,06	6,7	2,72			12,4	-0,56	6,3
4,2	-6,3	-0,9	-1,1			-0,65	4,4	1,5
0,6	6,8	-0,82	0,83			1,5	2,1	1,7
Δ=	233,3						1,6337
Δx1=	-119,4		x1=Δx1/Δ=	-0,512
Δx2=	-95,08		x2=Δx2/Δ=	0,7963
Δx3=	1,6337		x3=Δx3/Δ=	-0,017

б) з допомогою функції solve Matlab,

>> [a,b,c]=solve('1.2*a-1.06*b+6.7*c=2.72', '4.2*a-6.3*b-0.9*c=-1.1', '0.6*a+6.8*b-0.82*c=0.83')

a =

0.076445952804348415640969017925979

b =

0.1657805287031568136648390951672

c =

0.41850630105375046622620397303971

в) командним способом в Matlab.

>> a1=[1.2;4.2;0.6];

>> a2=[1.06;-6.3;6.8];

>> a3=[6.7;-0.9;-0.82];

>> A=[a1 a2 a3]

A =

1.2000 1.0600 6.7000

4.2000 -6.3000 -0.9000

0.6000 6.8000 -0.8200

>> a3=[6.7;-0.9;-0.82];

>> B=[2.72;-1.1;0.83]

B =

2.7200

-1.1000

0.8300

>> DA=det(A)

DA =

233.2994

>> A1=[B,a2,a3]

A1 =

2.7200 1.0600 6.7000

-1.1000 -6.3000 -0.9000

0.8300 6.8000 -0.8200

>> DA1=det(A1)

DA1 =

13.8683

>> A2=[a1,B,a3]

A2 =

1.2000 2.7200 6.7000

4.2000 -1.1000 -0.9000

0.6000 0.8300 -0.8200

>> DA2=det(A2)

DA2 =

37.6559

>> A3=[a1,a2,B]

A3 =

1.2000 1.0600 2.7200

4.2000 -6.3000 -1.1000

0.6000 6.8000 0.8300

>> DA3=det(A3)

DA3 =

86.2712

>> a=DA1/DA

a =

0.0594

>> b=DA2/DA

b =

0.1614

>> c=DA3/DA

c =

0.3698

>> a1=[6.7,-0.6,0.83];

>> a2=[0.8,1.1;5.2];

>> a3=[1.2;-5.4;-3.2];

>> A=[a1;a2;a3]

A =

6,70	-0,6	-0,83
0,8	1.1	-7,2
1,2	-5,4	0,54

>> B=[6.8;5.2;-3.2];

>> DA=det(A)

DA =

355.3501

>> A1=[B,a2,a3]

A1 =

6,8	-0,6	-0,83
5,2	1.1	-7,2
-3,2	-5,4	0,54

>> DA1=det(A1)

DA1 =

122.1733

>> A2=[a1,B,a3]

A2 =

6,70	6,8	-0,83
0,8	5,2	-7,2
1,2	-3,2	0,54

>> DA2=det(A2)

DA2 =

-120.0038

>> A3=[a1,a2,B]

A3 =

6,70	-0,6	6,8
0,8	1.1	5,2
1,2	-5,4	-3,2

>> DA3=det(A3)

DA3 =

206.0200

>> x1=DA1/DA

x1 =

1.1438

>> x2=DA2/DA

x2 =

0.79

>> x3=DA3/DA

x3 =

-0.4712

Аналітичний розвязок	Командним способом в Matlab	Розв’язок з допомогою функції solve Matlab
1.14	1.14	1.14
0.79	0.79	0.79
-0,47	-0,47	-0,47

Висновок:

Результати розв’язання системи рівнянь аналітичним способом в Exel, командним способом в Matlab та з допомогою функції solve в Matlab співпадають, тобто система розв’язана вірно.

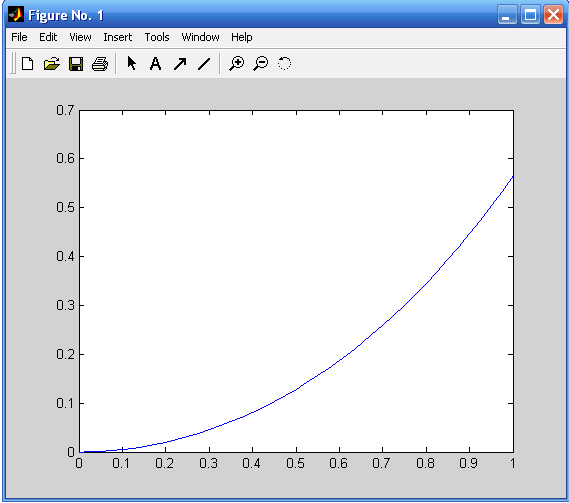
1.4 Чисельне рішення звичайних диференціальних рівнянь

Побудувати графік і вивести у вигляді таблиці розв’язок задачі Коші на інтервалі [0; 1] методом Рунге-Кутта 4-го порядку.

№ п/п	f(x,y)	уо
12.		0.0

Розв’язок:

М-Файл оформляється :

function dydx = F(x,y)

dydx = zeros(1,1);

dydx(1) =(exp(-y)+exp(x)-2)

end

Чисельний розв’язок задачі Коші:

>> [X Y]=ode45(@F,[0 1],[0])

>> [X,Y]

ans =

ans = 0 0

0.0250 0.0003

0.0500 0.0013

0.0750 0.0028

0.1000 0.0050

0.1250 0.0078

0.1500 0.0113

0.1750 0.0154

0.2000 0.0201

0.2250 0.0254

0.2500 0.0314

0.2750 0.0381

0.3000 0.0454

0.3250 0.0534

0.3500 0.0620

0.3750 0.0713

0.4000 0.0813

0.4250 0.0920

0.4500 0.1034

0.4750 0.1155

0.5000 0.1284

0.5250 0.1419

0.5500 0.1563

0.5750 0.1714

0.6000 0.1873

0.6250 0.2039

0.6500 0.2214

0.6750 0.2398

0.7000 0.2590

0.7250 0.2791

0.7500 0.3001

0.7750 0.3220

0.8000 0.3448

0.8250 0.3687

0.8500 0.3935

0.8750 0.4194

0.9000 0.4463

0.9250 0.4744

0.9500 0.5036

0.9750 0.5339

1.0000 0.5655

Побудова графіка чисельного рішення задачі Коші: