10. Построить следующие анимации, используя разные системы координат:
10.1.
,
,
.
> restart;
> with(plots):
Warning, the name changecoords has been redefined
> x:=3/2*cos(t+u)^3;
y:=sin(t+u)+2/3*cos(2*t+u);
animate([x,y,u=-Pi..Pi],t=1..20,color=PLUM,thickness=2);
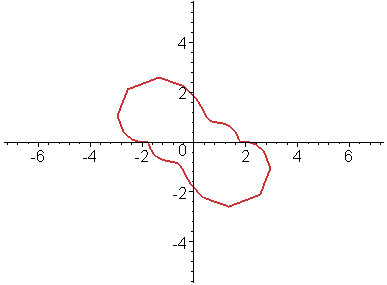
Приведём первый, третий и пятый кадры анимации:
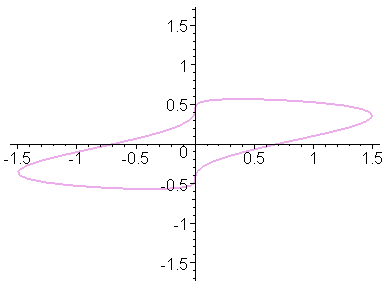
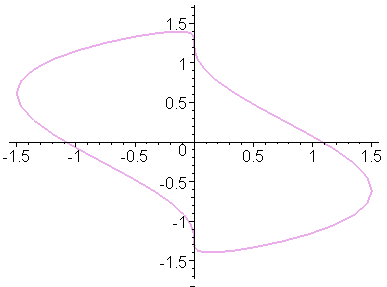
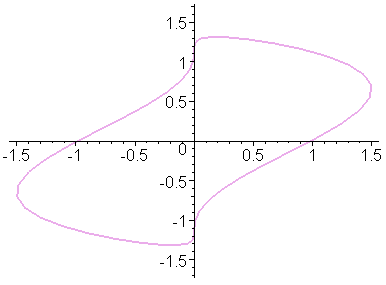
Построим эту же анимацию, используя полярную и биполярную системы координат.
> animate([x,y,u=-Pi..Pi],t=1..20,color=GOLD,thickness=2,coords=polar);
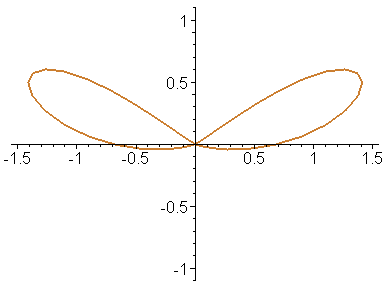
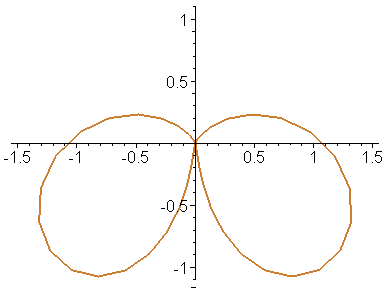
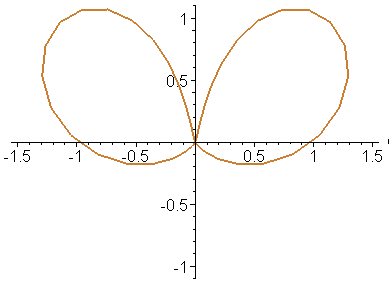
> animate([x,y,u=-Pi..Pi],t=1..20,color=ORANGE,thickness=2,coords=bipolar);
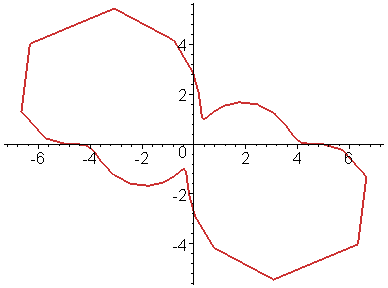
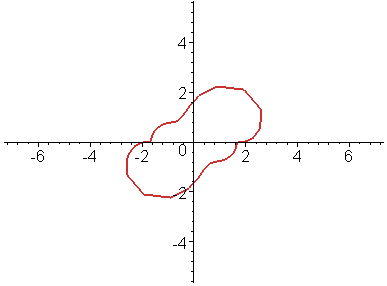
10.2.
,
,
,
.
> restart;
> with(plots):
Warning, the name changecoords has been redefined
> x:=u*cos(v+t);
y:=u*sin(v+t);
z:=v+t;
> animate3d([x,y,z],u=0..4,v=0..10,t=0..20,shading=XYZ,style=PATCHNOGRID);
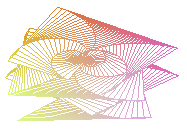
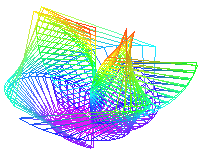
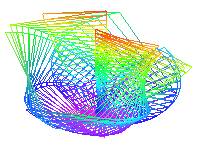
Приведём первый, третий и пятый кадры анимации:
Построим эту же анимацию в цилиндрической и сферической системе координат.
> animate3d([x,y,z],u=0..4,v=0..10,t=0..20,shading=XY,style=HIDDEN,coords=cylindrical);
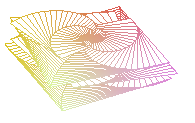
> animate3d([x,y,z],u=0..4,v=0..10,t=0..20,shading=ZHUE,style=WIREFRAME,coords=spherical);
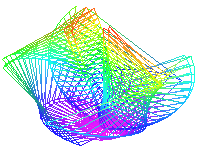
11. Исследовать функцию на непрерывность. Построить график.
> restart;
> f:=piecewise(x<=-2,x^2,x>-2 and x<=2,-x+2,x>2,4*sin(Pi*x)+1);
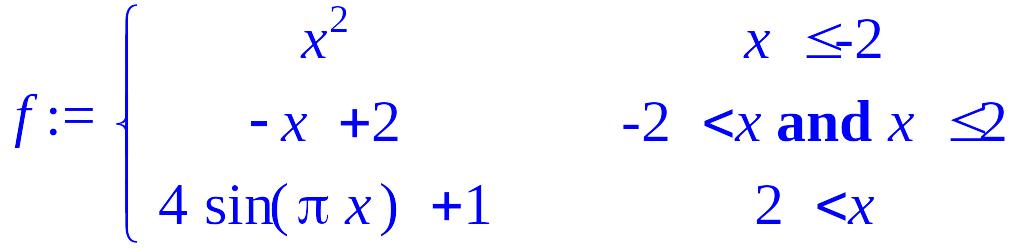
> x1:=-2;
> F(x1)=evalf(subs(x=x1,f));
Limit(F,x=x1)=limit(f,x=x1);
Limit(F,x=x1,left)=limit(f,x=x1,left);
Limit(F,x=x1,right)=limit(f,x=x1,right);
В точке функция непрерывна.
> x2:=2;
> F(x2)=evalf(subs(x=x2,f));
Limit(F,x=x2)=limit(f,x=x2);
Limit(F,x=x2,left)=limit(f,x=x2,left);
Limit(F,x=x2,right)=limit(f,x=x2,right);
Пределы справа и
слева конечны, но не равны между собой,
поэтому в точке
функция
имеет разрыв первого рода.
> plot(f,x=-3..5,discont=true,color=TAN,thickness=2);
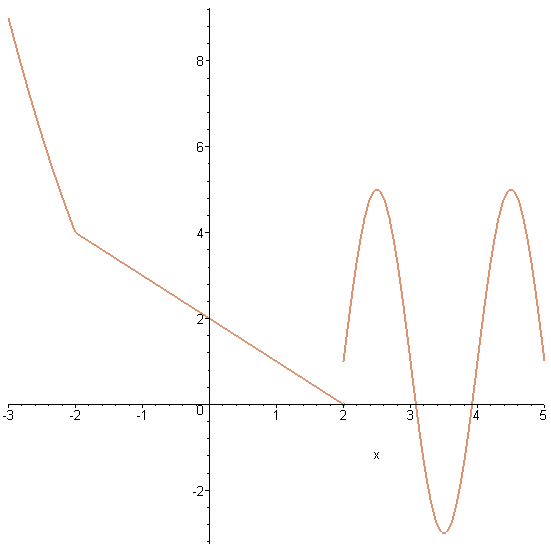
12. Найти производные указанного порядка.
12.1. , Найти и .
> restart;
> y:=x*(x+2)^2*(x+3)^3*(x+4)^4;
> Diff(Y,x$6)=simplify(diff(y,x$6));
> Diff(Y,x$10)=diff(y,x$10);
12.2. , Найти .
> restart;
> y:=sinh(3*x)+4*sin(2*x);
> Diff(Y,x$5)=simplify(diff(y,x$5));
