2

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ УКРАИНЫ

ДОНЕЦКИЙ НАЦИОНАЛЬНЫЙ УНИВЕРСИТЕТ

КАФЕДРА ПРИКЛАДНОЙ МЕХАНИКИ И

КОМПЬЮТЕРНЫХ ТЕХНОЛОГИЙ

ОТЧЁТ

По вычислительной практике

Выполнил:

студент математического

факультета, группы 2-З

Иванов Иван Иванович

Руководитель практики:

проф. Гольцев А.С.

Донецк – 2013

Вариант 0

Используя систему аналитических вычислений Maple, выполнить следующие вычисления:

1. Вычислить:

1. ;

2. ;

3. ;

4. ;

5. ;

6. , ;

7. ;

8. ;

9. ;

10. ;

11. ;

12. ;

13. , .

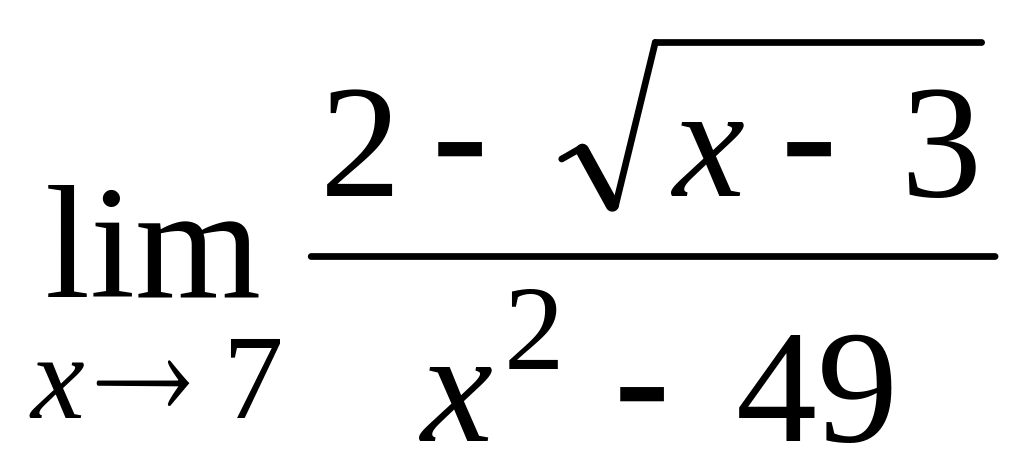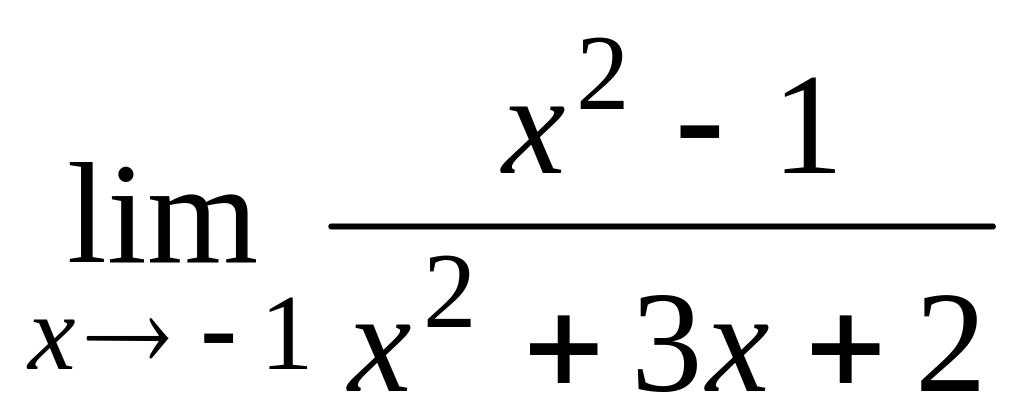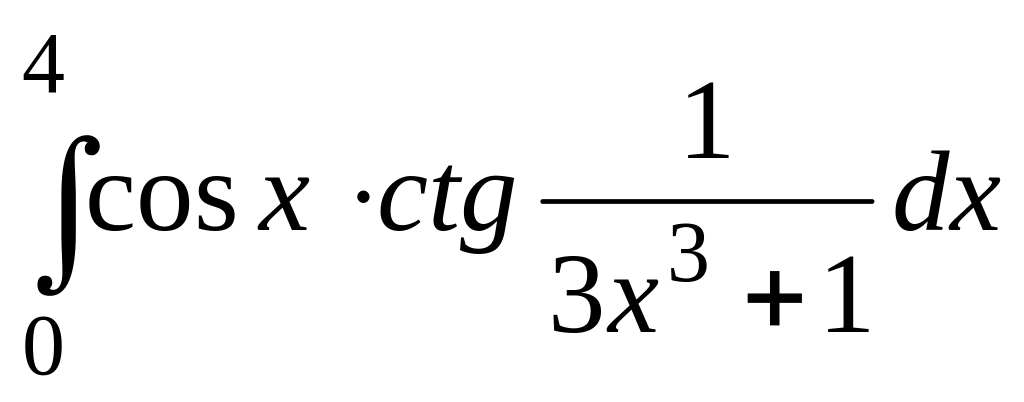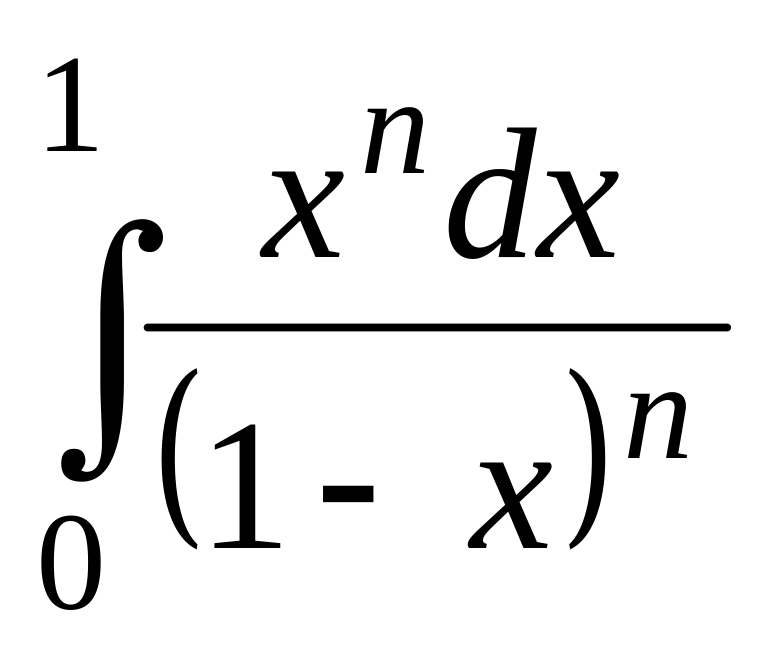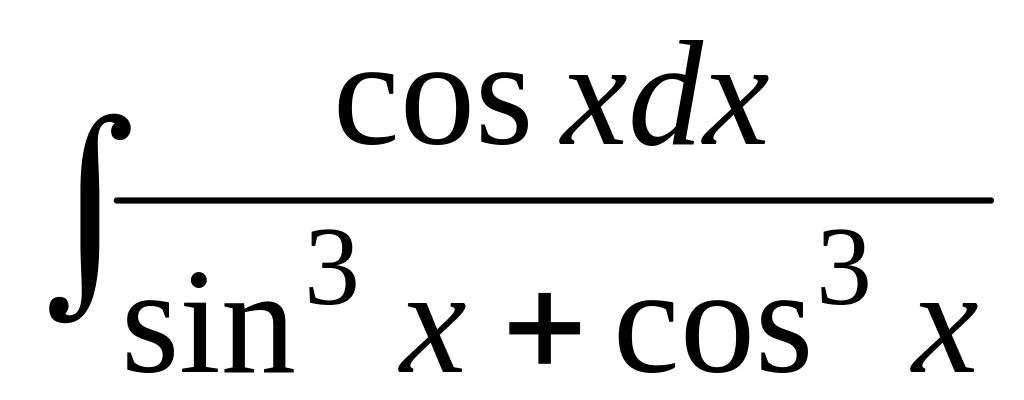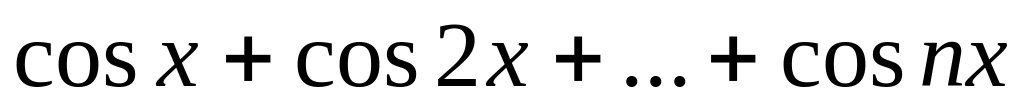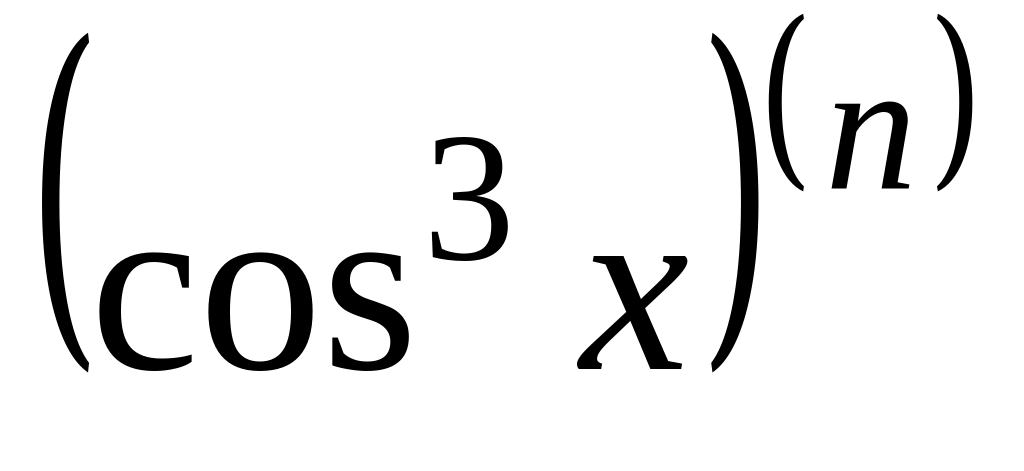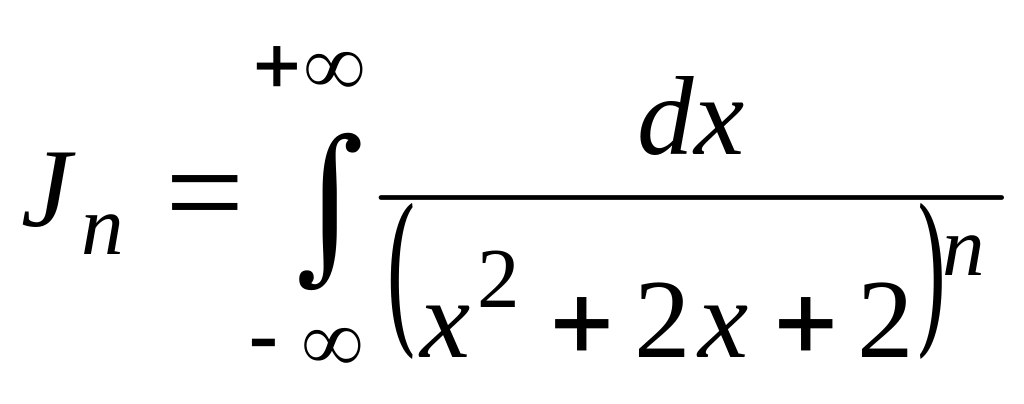2. Решить системы уравнений двумя различными способами:

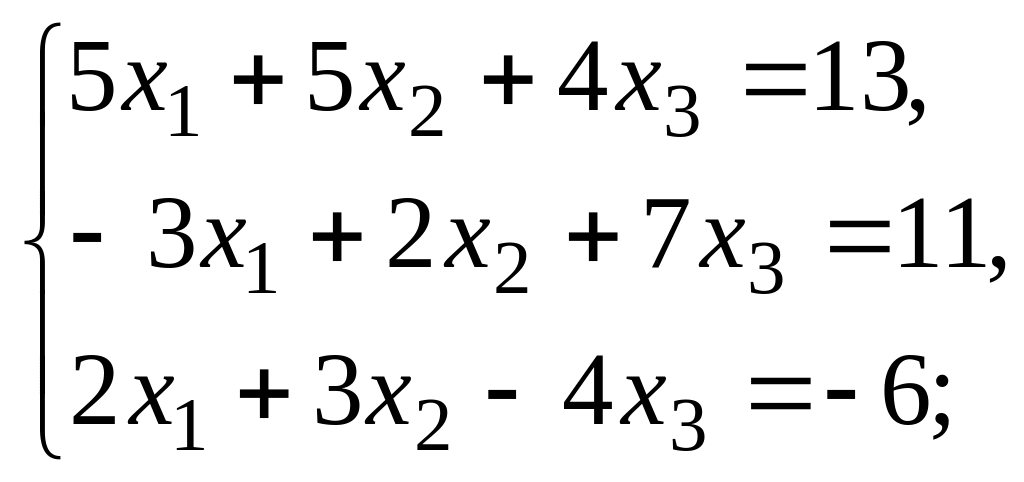   1. 2.2.

3. 

3. Исследовать функцию на непрерывность в заданных точках:

   1. ; , .

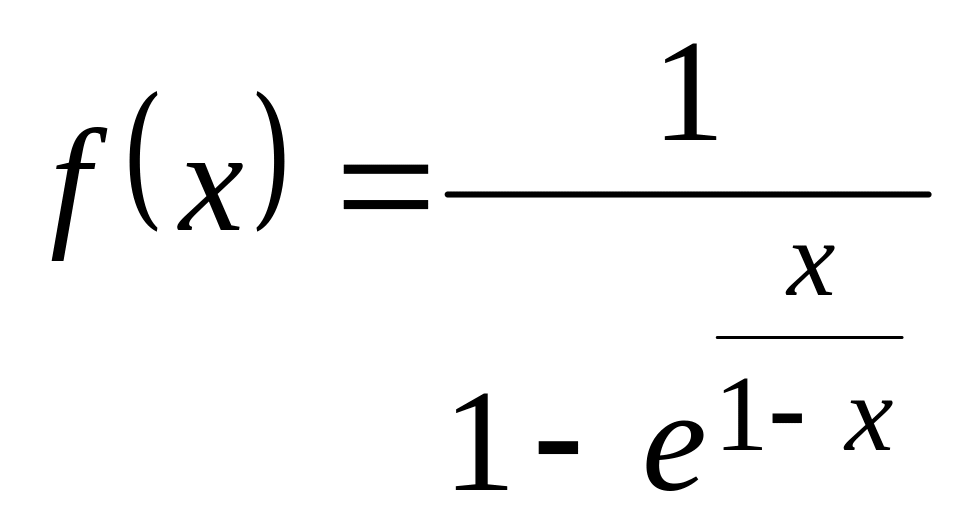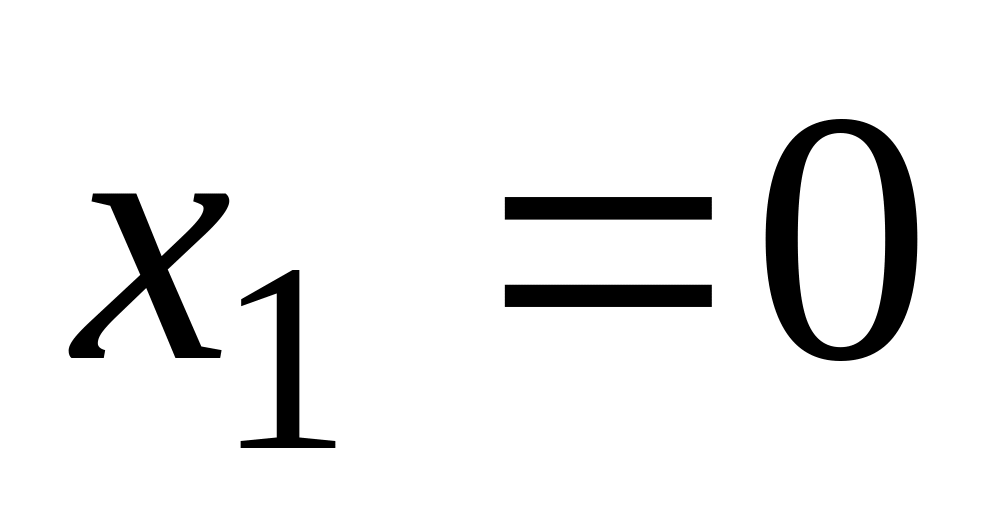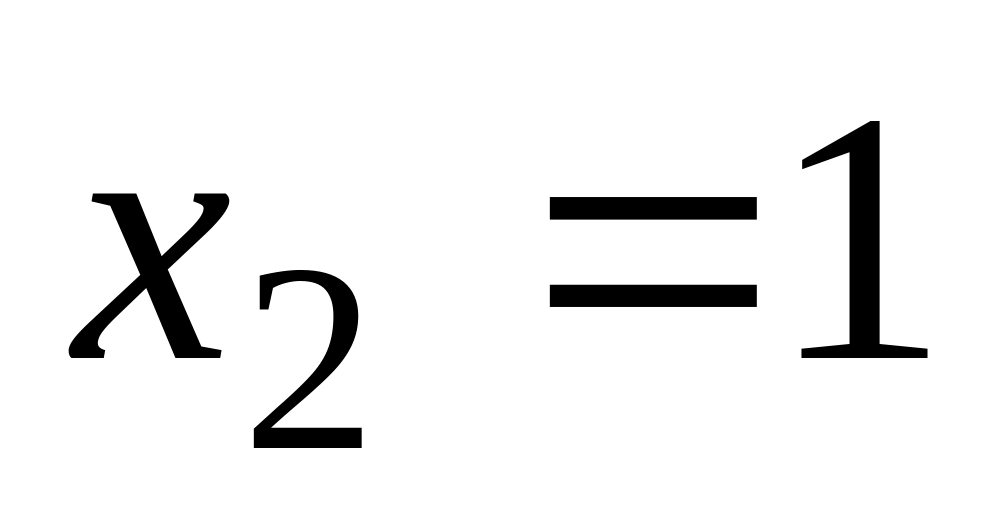4. Исследовать на непрерывность и нарисовать эскизы графиков следующих функций:

   1. ;

   2. ;

   3. .

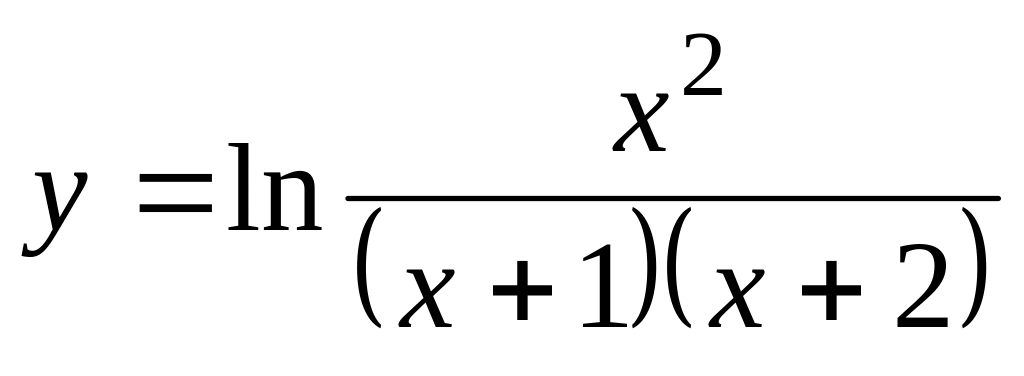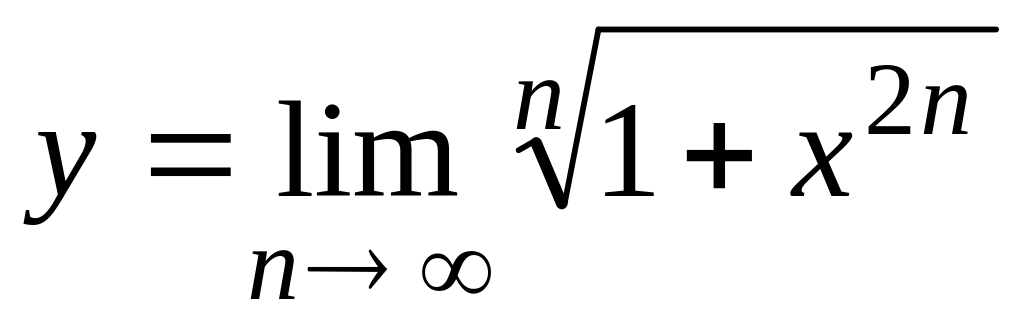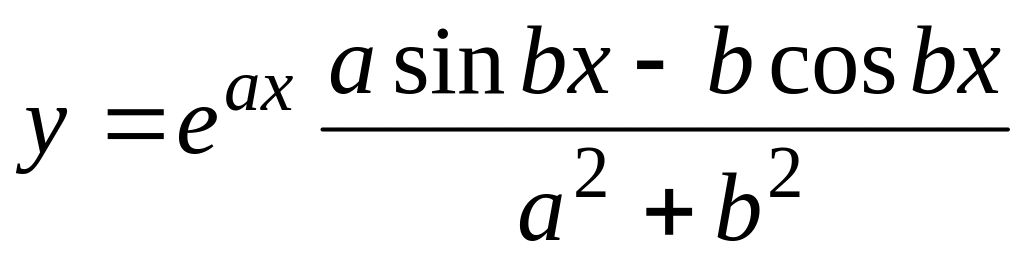5. Вычислить производную:

   1. ;

   2. ;

   3. .

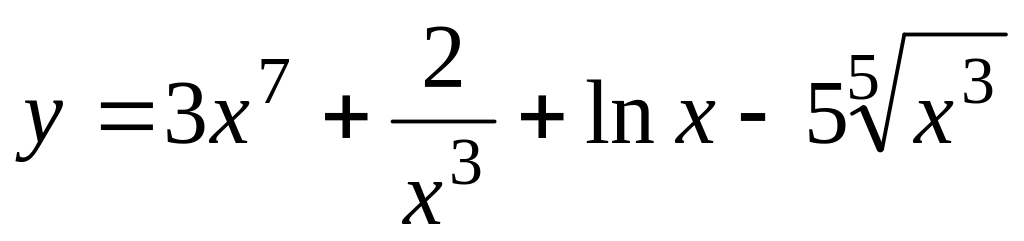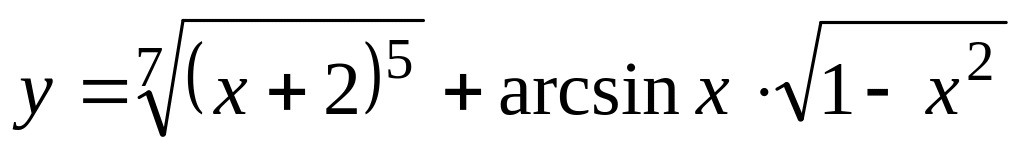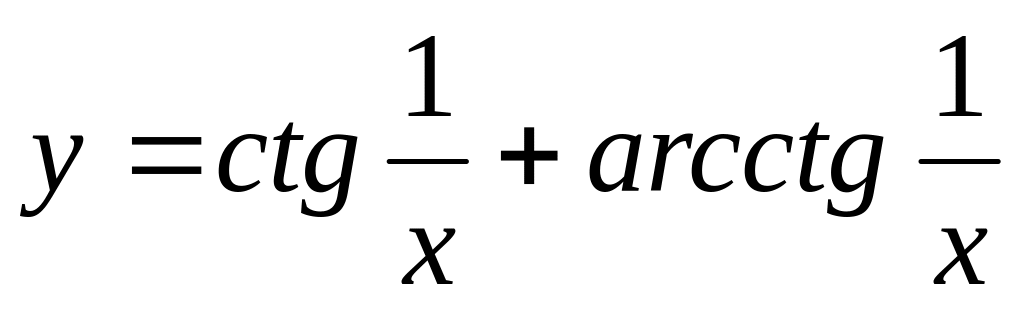6. Построить график поверхности:

   1. .

7. Даны вектора 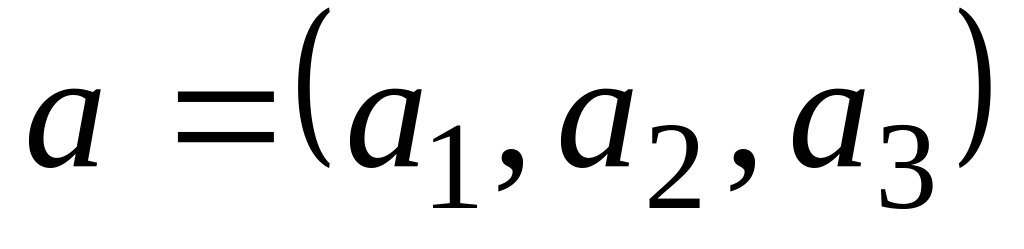, , 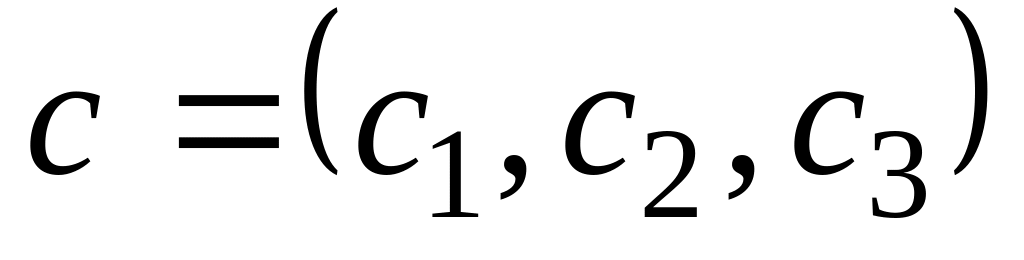. Определить:

   1. длину вектора : ;

   2. скалярное произведение ;

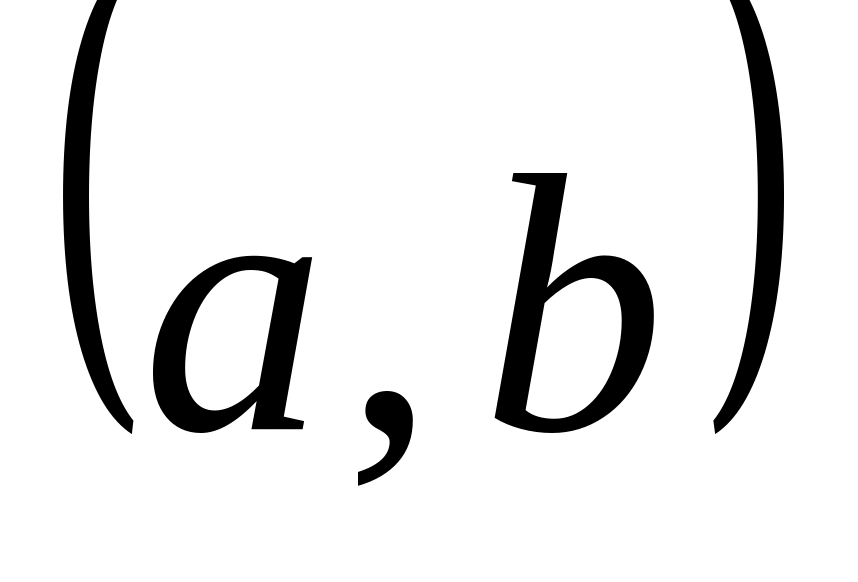   3. косинус угла между векторами и ;

   4. векторное произведение ; ;

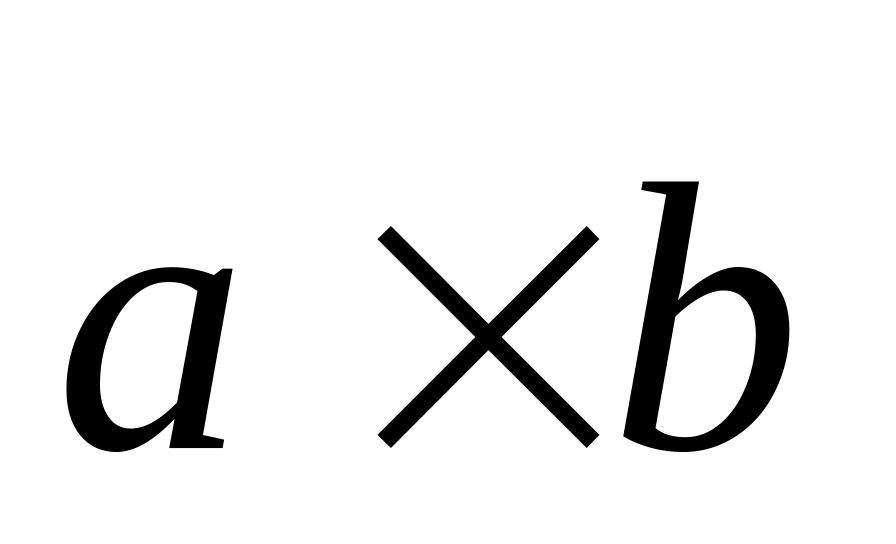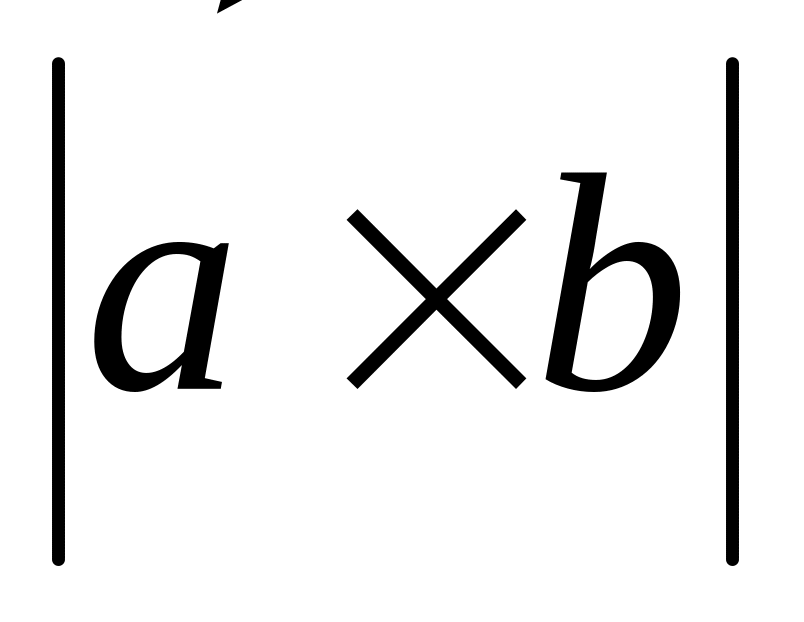   5. смешанное произведение векторов , , ;

   6. определить коллинеарность векторов и ;

   7. определить компланарность векторов , , ;

   8. построить заданные вектора.

, , .

8. На одном рисунке изобразить график функции 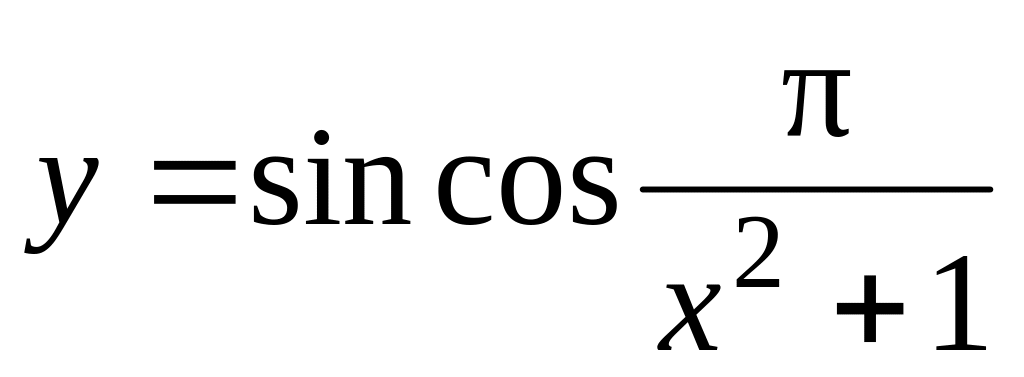, её производной и касательной в точке .

9. Найти решение задачи Коши для дифференциального уравнения и системы дифференциальных уравнений. Проверить полученный результат. Построить графики полученных решений.

   1. , , ;

   2. , , .

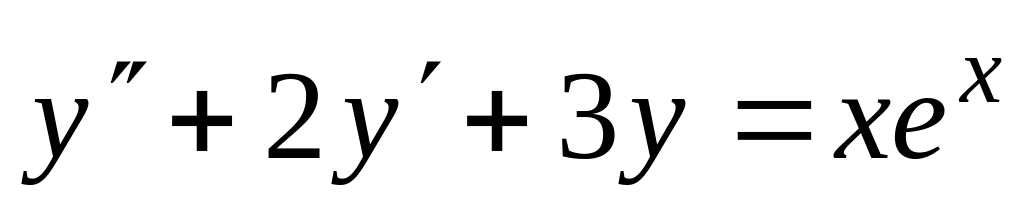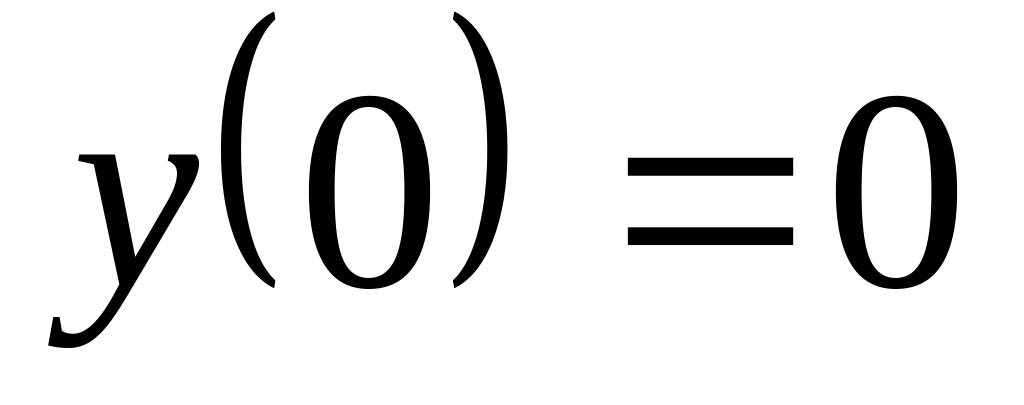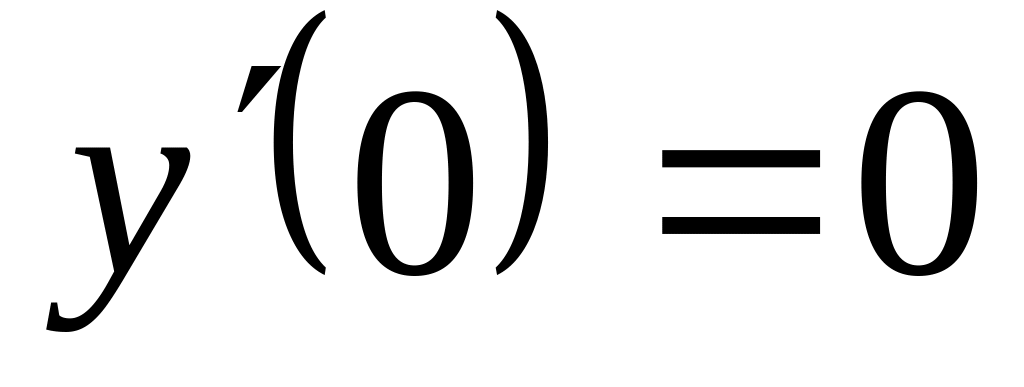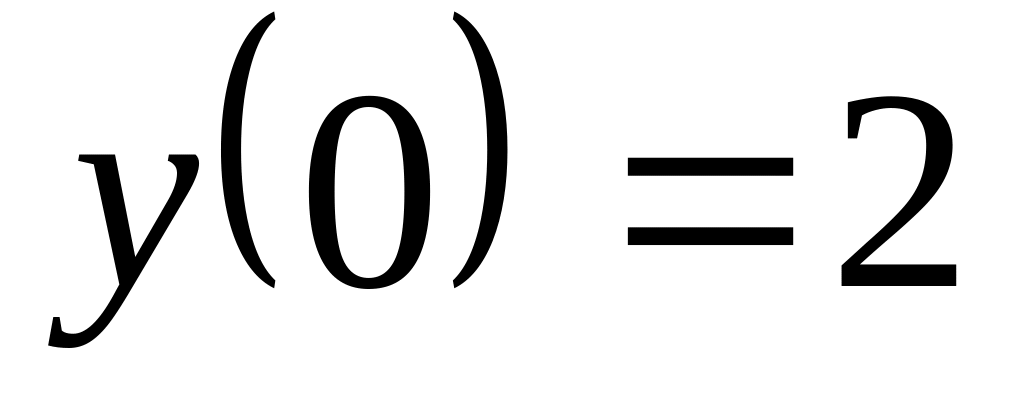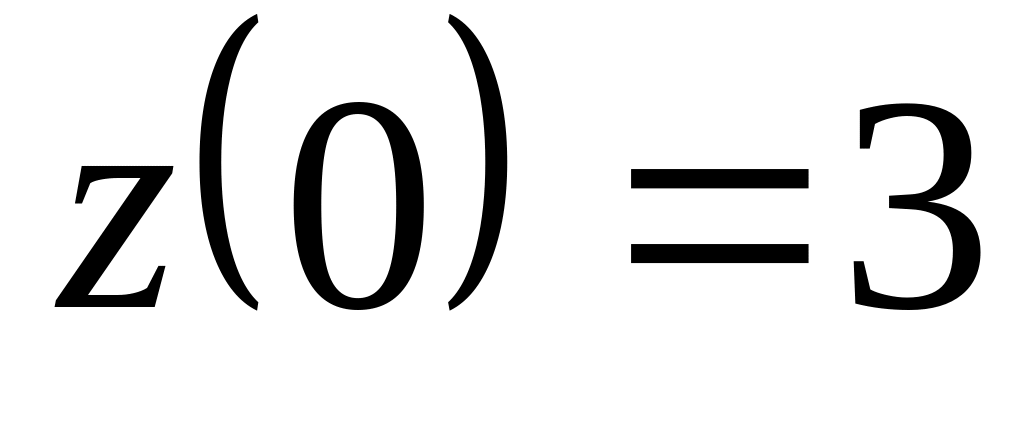10. Построить следующие анимации, используя разные системы координат:

    1. , , ;

    2. , , , .

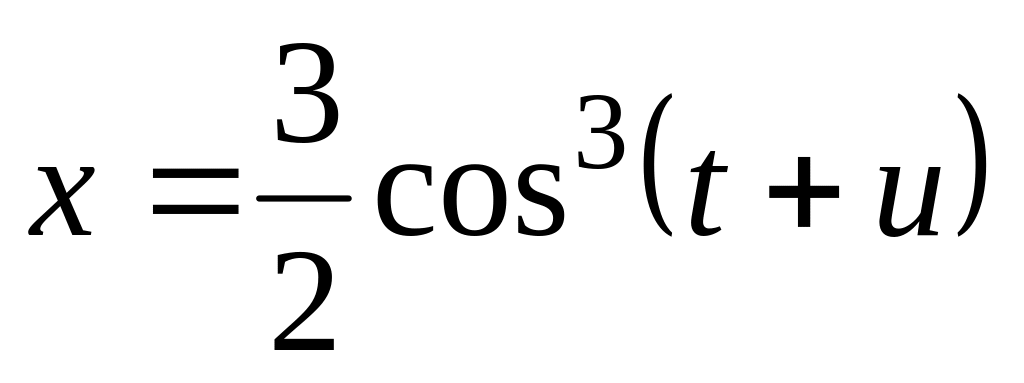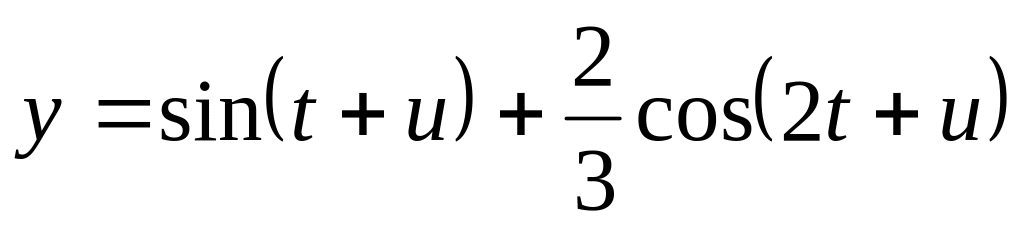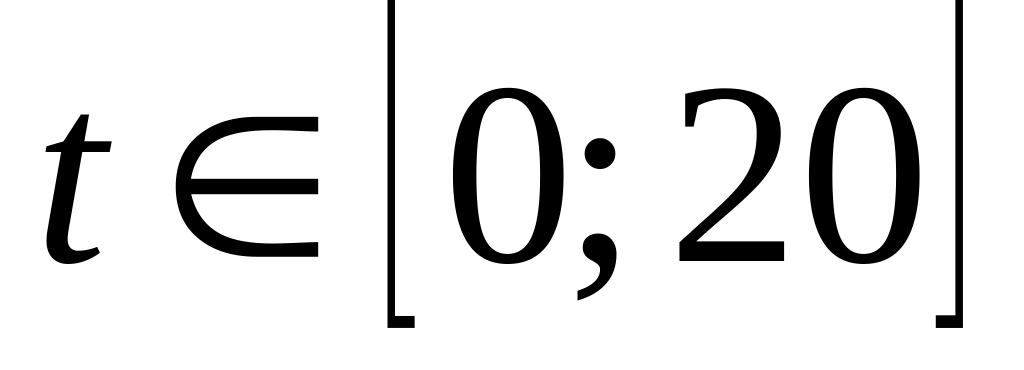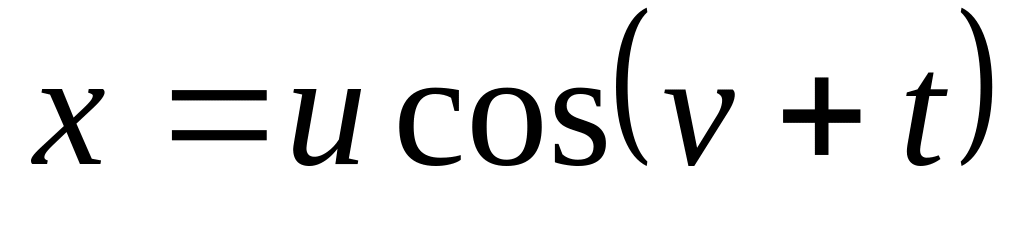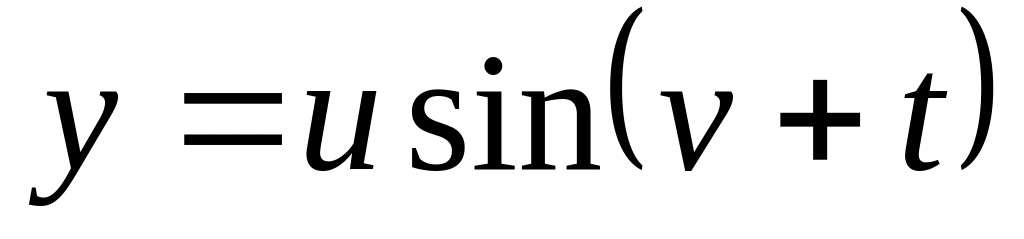11. Исследовать функцию на непрерывность. Построить график.

12. Найти производные указанного порядка

    1. , найти и ;

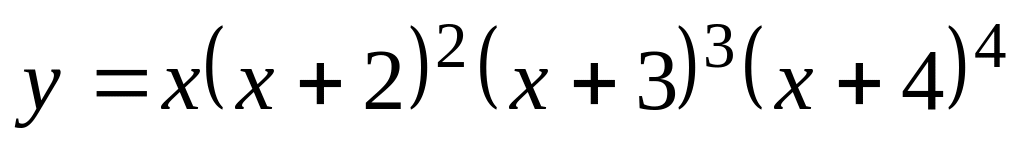    2. , найти .

1. Вычислить

1.1. .

> restart;

> Limit((tan(x)-sin(x))/x^3,x=0)=limit((tan(x)-sin(x))/x^3,x=0);

1.2. .

> Limit((2-sqrt(x-3))/(x^2-49),x=7)=limit((2-sqrt(x-3))/(x^2-49),x=7);

1.3. .

> Limit((x^2-1)/(x^2+3*x+2),x=-1)=limit((x^2-1)/(x^2+3*x+2),x=-1);

1.4. .

> Limit(sin(x-5)/(x^2-25),x=5)=limit(sin(x-5)/(x^2-25),x=5);

1.5. .

> Int(cos(x)*cot(1/(3*x^3+1)),x=0..4);

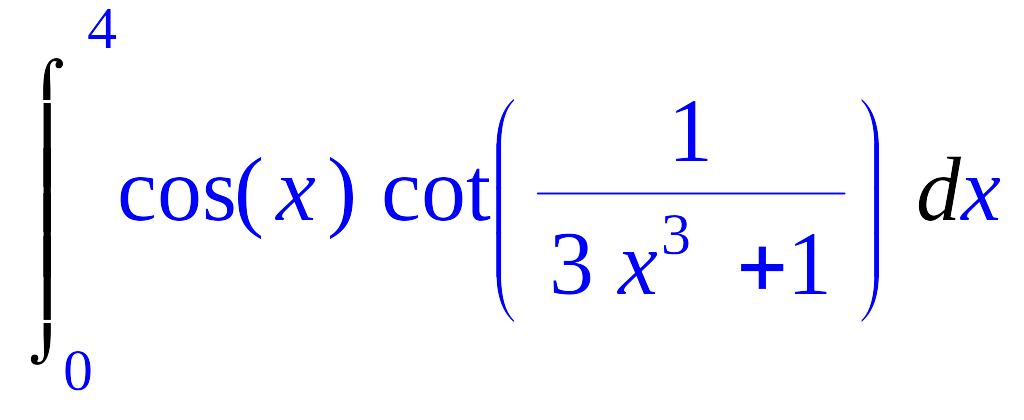
> evalf(%);

1.6. , .

> restart;

> assume(n>-1,n<1);

> Int(x^n/(1-x)^n,x=0..1)=int(x^n/(1-x)^n,x=0..1);

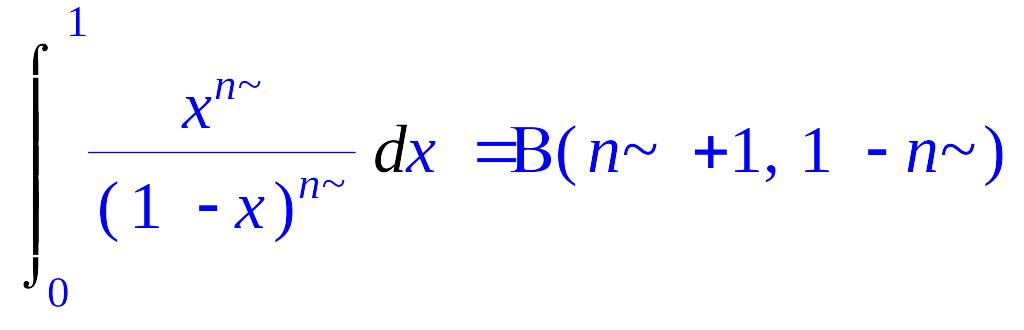
1.7. .

> restart;

> Int(cos(x)/(sin(x)^3+cos(x)^3),x)=int(cos(x)/(sin(x)^3+cos(x)^3),x);

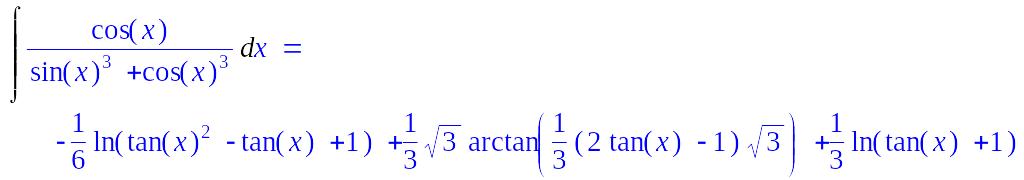
1.8. .

> restart;

> Sum(cos(k*x),k=1..n)=sum(cos(k*x),k=1..n);

1.9. .

Рассмотрим функцию , которую представим в виде:

.

Или то же самое средствами Maple:

> restart;

>

> y:=cos(x)^3;

Представим функцию y в следующем виде: =

> s:=trigsubs(cos(x)**2);

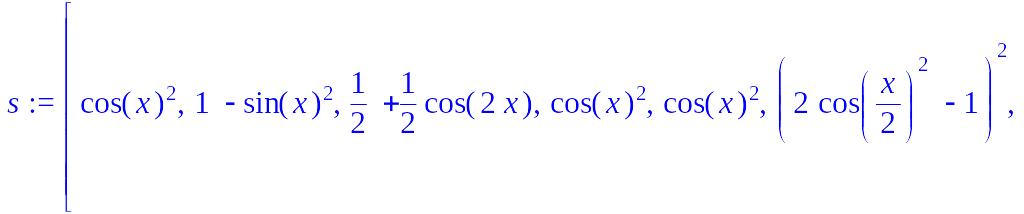
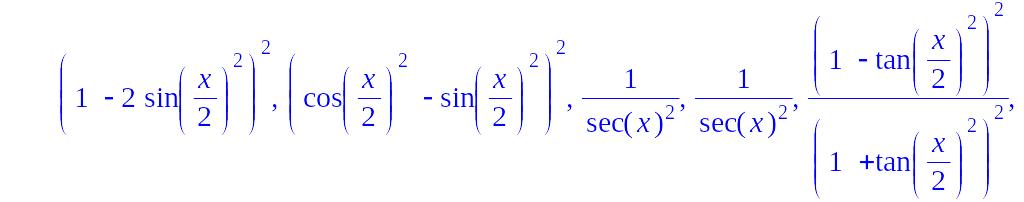
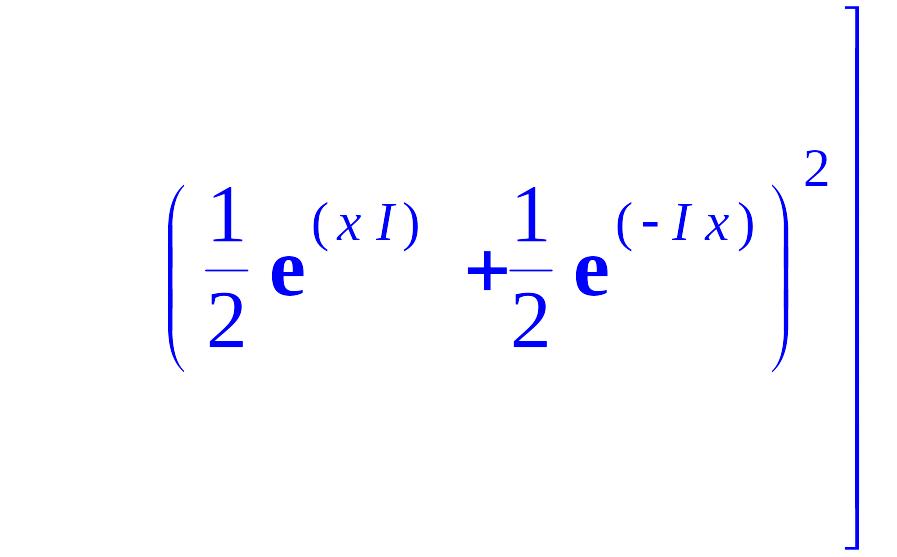
> s[3]*cos(x);

> s1:=trigsubs(cos(2*x)*cos(x));

> y:=1/2*s1[1]+1/2*cos(x);

Рассмотрим функцию y1 = и найдём с помощью Maple её первые 4 производные:

> y1:=cos(k*x);

> diff(y1,x);

diff(y1,x$2);

diff(y1,x$3);

diff(y1,x$4);

Отсюда видно, что

.

Определим процедуру с одним формальным параметром для нахождения n-й производной от функции .

> diff_y1_n:=k->k^n*cos(k*x+n*Pi/2);

Имеем

.

> diff_y_n:=3/4*diff_y1_n(1)+1/4*diff_y1_n(3);

1.10.

Представим функцию в виде разности элементарных дробей:

.

Проверяем полученный результат в Maple

> restart;

> y:=1/(x^2-17*x+72);

> is(y=1/(x-9)-1/(x-8));

Рассмотрим функцию и найдём с помощью Maple её первые 3 производные:

> y1:=1/(x-a);

> diff(y1,x);

diff(y1,x$2);

diff(y1,x$3);

Отсюда видно, что

.

Определим процедуру с одним формальным параметром для нахождения n-й производной от функции .

> diff_y1_n:=a->(-1)^n*n!/(x-a)^(n+1);

Имеем

.

> diff_y_n:=diff_y1_n(9)-diff_y1_n(8);

1.11.

> restart;

> I1:=Int(1/(x^2+2*x+2)^n,x=-infinity..infinity);

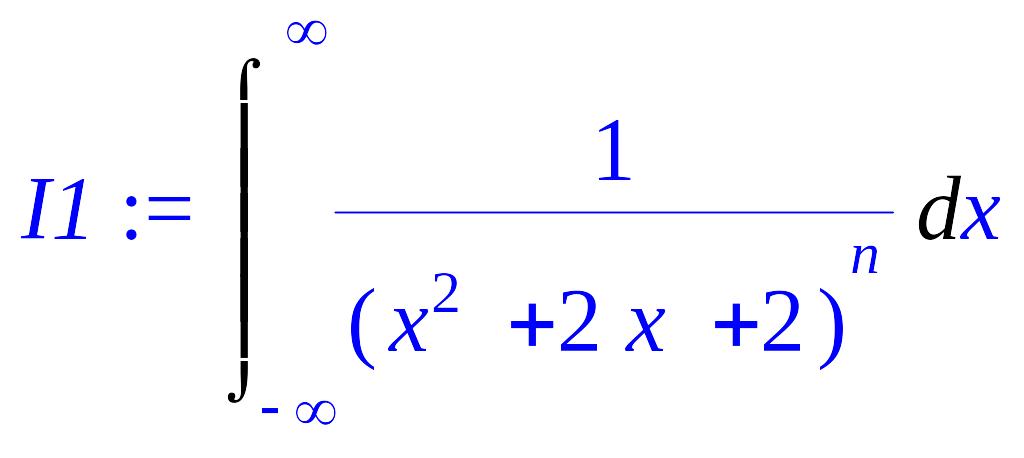
> I1:=int(1/(x^2+2*x+2)^n,x=-infinity..infinity);

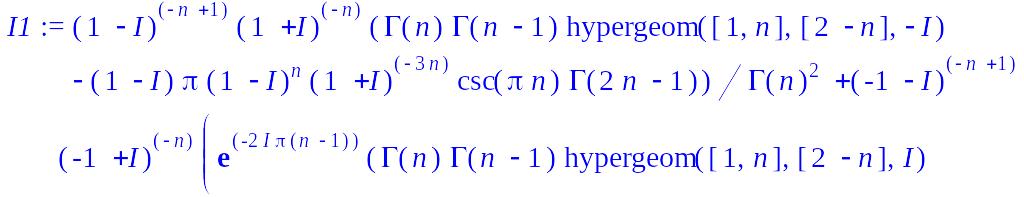
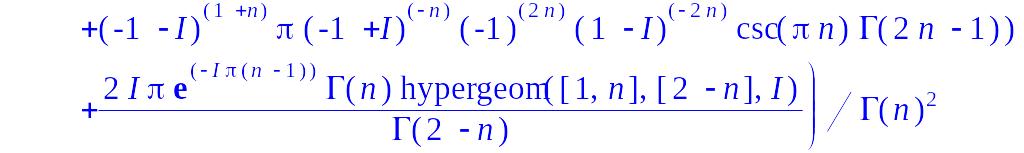
> I1:=evaln(I1):

С целью получения менее громоздкого выражения преобразуем исходный интеграл таким образом:

.

> I2=Int(1/(t^2+1)^n,t=-infinity..infinity);

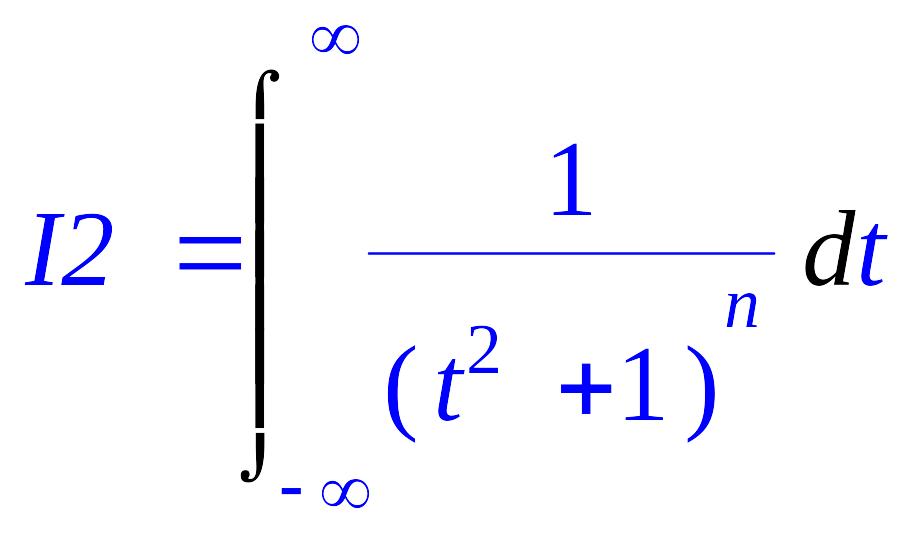
> I2:=int(1/(t^2+1)^n,t=-infinity..infinity);

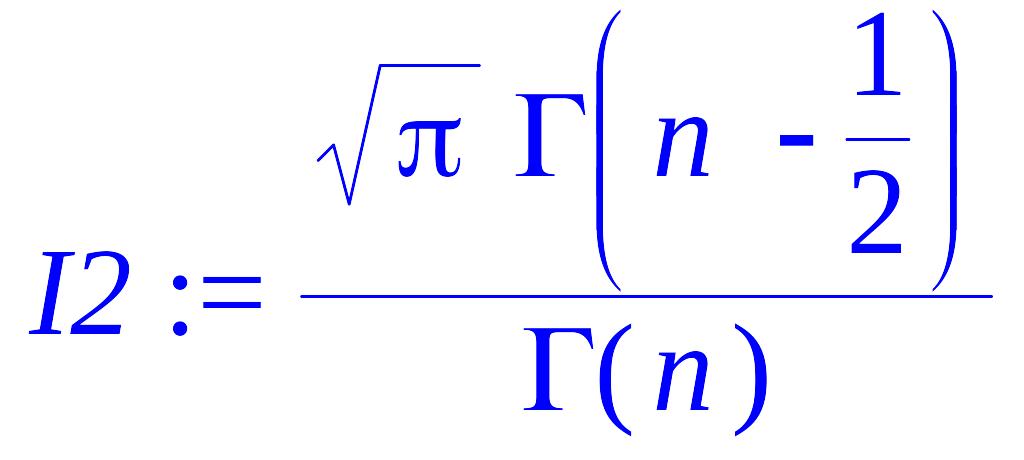
> I1=I2;

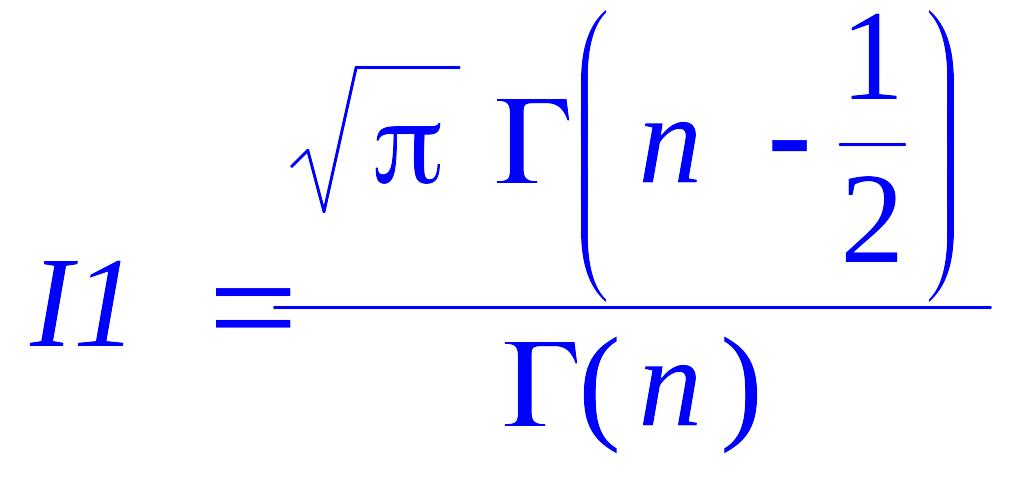
1.12.

.

Обозначим , т.е. .

Таким образом, для нахождения нужно решить уравнение .

Построим графики функций и средствами Maple:

> restart;

> plot([cos(u),u],u=-5..5,color=[MAGENTA,KHAKI],thickness=2);

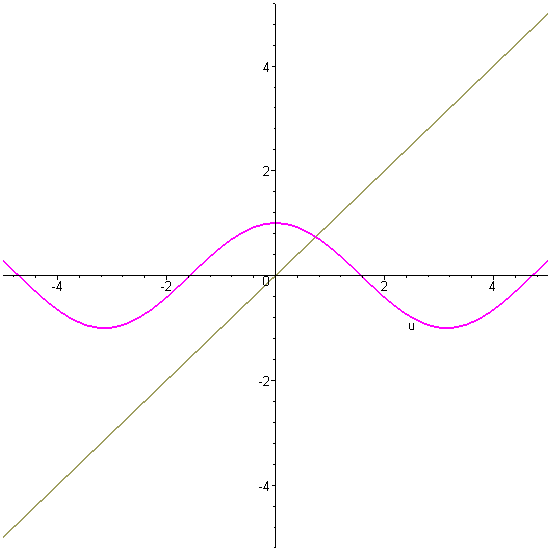
Отсюда видно, что уравнение имеет единственное решение. Найдём его:

> fsolve(cos(u)=u,u);

1.13.

> restart;

> limit((sqrt(x)-sqrt(a)-sqrt(x-a))/sqrt(x^2-a^2), x = a, complex);