34. Чертежи призм и пирамид. Пересечение призм плоскостью

Фигура сечения прямой пятиугольной призмы фронтально-проецирующей плоскостью Р (рис. 178, а) представляет собой плоский пятиугольник 1 2 3 4 5.Для построения проекций фигуры сечения находят проекции точек пересечения плоскости Р с ребрами призмы и соединяют их прямыми линиями. Фронталь¬ные проекции этих точек получаются при пересечении фронтальных проекций ребер призмы с фронтальным следом Pv секущей плоскости Р (точки Г — 5').Горизонтальные проекции точек пересечения 1—5 совпадают с горизонтальными проекциями ребер. Имея две проекции этих точек, с помощью линий связи находят профильные проекции 1"—5". Полученные точки 1"—5" соединяют прямыми линиями и получают профильную проекцию фигуры сечения.Действительный вид фигуры сечения можно определить любым из способов: вращения, совмещения или перемены плоскостей проекций (см. гл. 15).В данном примере (рис. 27, а) применен способ перемены плоскостей проекций. Горизонтальная плоскость проекций заменена новой Нр причем ось х, (для упрощения построений) совпадает с фронтальным следом плоскости Р.Для нахождения новой горизонтальной проекции какой-либо точки фигуры сечения (например, точки 1) необходимо выполнить следующие построения. Из точки Г восставляют перпендикуляр к новой оси х1 и откладывают на нем расстояние от прежней оси х до прежней горизонтальной проекции точки 1, т. е. отрезок п. В результате получают точку 10. Так же находят и новые горизонтальные проекции точек 2—5. Соединив прямыми линиями новые горизонтальные проекции lg—50, получают действительный вид фигуры сечения.

35. Пересечение пирамиды плоскостью.

плоскость пересекает пирамиду по многоугольнику. Если плоскость параллельна основанию пирамиды, в сечении получается фигура, подобная основанию. При построении линии пересечения пирамиды с плоскостью определяют точки пересечения ее ребер с данной плоскостью или строят линии пересечения граней пирамиды с этой плоскостью.  Фронтальная проекция линии сечения совпадает с фронтальной проекцией На рис.6.1 показано построение проекции линии сечения пирамиды фронтально-проецирующей плоскостью _v  до пересечения с горизонтальными проекциями соответствующих рёбер пирамиды. ... бсекущей плоскости. Горизонтальная и профильная проекции сечения находятся с помощью линий связи проведённых из точек 1 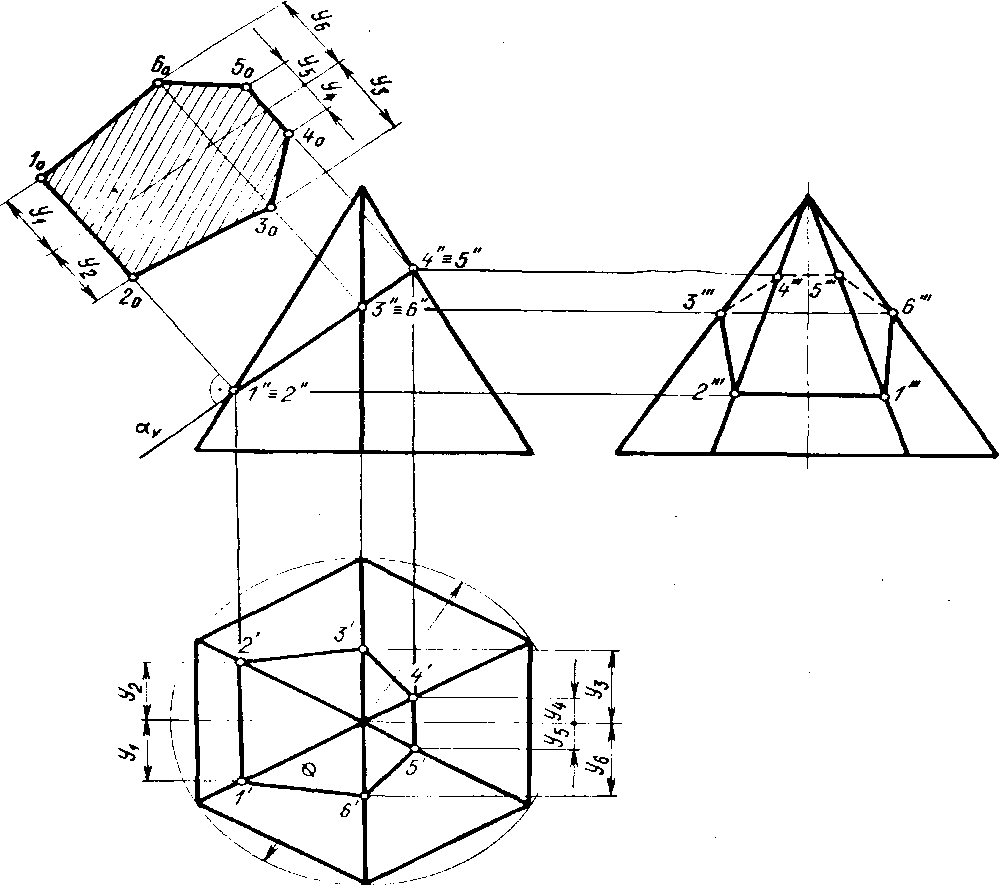Натуральная величина сечения определена способом замены плоскостей проекции. Так как сечение имеет фронтальную ось симметрии, при построении его натурального вида эта ось проведена параллельно _v. Для построения точек 1о...6о данного сечения использованы их размеры у. 36. Пересечение многогранников прямой линией.

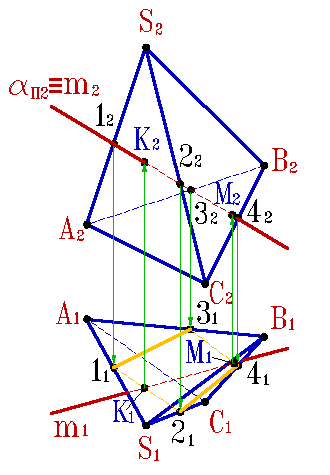
Для определения точек пересечения прямой линии с многогранником, задача сводится к нахождению точек пересечения прямой с плоскостями граней (рис.6.12).

Алгоритм решения задачи: 1. Провести плоскость : m. 2. Построить сечение многогранника плоскостью . Определить искомые точки К,М - пересечения  полученного сечения с прямой m.