- •1. Образование проекций. Проекции центральные и параллельные. Понятие однозначности объекта и чертежа. Метод Монжа
- •2. Точка в системе двух и трех плоскостей проекций. Ортогональные проекции и система прямоугольных координат.
- •4. Проекция отрезка прямой линии. Частные положения прямой линии относительно плоскостей проекций.
- •5. Точка на прямой. Следы прямой.
- •7. Взаимное положение двух прямых
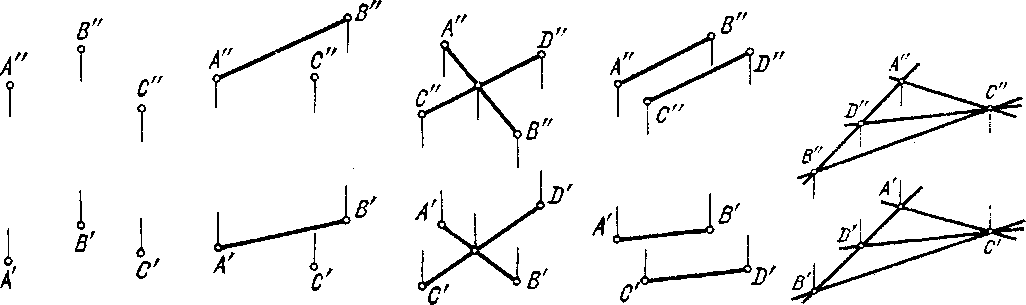
- •1. Параллельные прямые линии.
- •2. Пересекающиеся прямые.
- •3. Скрещивающиеся прямые
- •8. Проекциях плоских углов.
- •9. Различные способы задания плоскости на чертеже (включая следы плоскости).
- •10. Прямая и точка в плоскости. Прямые особого положения.
- •11. Положение плоскости относительно плоскостей проекций.
- •12. Плоскости частного положения, их свойства. Использование этих
- •13. Построение проекций плоских фигур. Плоские кривые
- •14. Пересечение прямой линии с проецирующей плоскостью.
- •15 Взаимнопересекающиеся плоскости.
- •17. Пересечение прямой линии с плоскостью общего положения.
- •18. Построение линии пересечения двух плоскостей по точкам пересечения прямых линий с плоскостью
- •31. Вращение вокруг осей, параллельных плоскостям проекций.
- •32. Определение натуральной величины плоской фигуры вращением вокруг фронтами или горизонтали.
- •33. Способ совмещения. Определения натуральной величины плоской фигуры распложенной в плоскости.
- •34. Чертежи призм и пирамид. Пересечение призм плоскостью
- •35. Пересечение пирамиды плоскостью.
- •37. Развертывание поверхностей многогранников.
- •38.Цилиндрические и конические винтовые линии.
- •39. Общие сведенья о кривых поверхностях. Обзор кривых поверхностей, их задание и изображение на чертеже.
- •40. Поверхности вращения.
- •41. Винтовые поверхности и винты
- •42. Проведение плоскостей, касательных к кривым поверхностям.
- •43. Пересечение цилиндрической поверхности плоскостью. Построение развертки
- •45. Пересечение кривых поверхностей с кривой линией
- •46. Построение линии взаимного пересечения поверхностей способом вспомогательных секущих плоскостей.
- •47. Применения вспомогательных секущих сфер при построении линии пересечения поверхностей вращения.
- •48. Примеры построения разверток поверхностей
- •7.1. Построение разверток многогранников
- •7.2. Построение разверток кривых развертывающихся поверхностей
- •7.3. Построение условных разверток неразвертывающихся поверхностей
- •49. Аксонометрические проекции
9. Различные способы задания плоскости на чертеже (включая следы плоскости).
Положение плоскости в пространстве определяется:
а) тремя точками, не лежащими на одной прямой линий, б) прямой и точкой, взятой вне прямой, в) двумя пересекающимися прямыми, г) двумя параллельными прямыми.
В соответствии с этим на чертеже плоскость может быть задана:
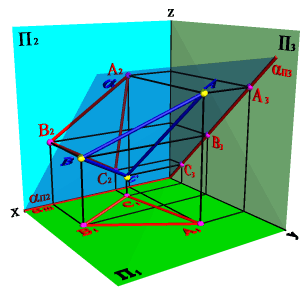
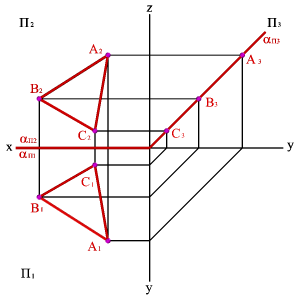
а) проекциями трех точек, не лежащих на одной прямой (рис. 97), б) проекциями прямой и точки, взятой вне прямой (рис. 98), в) проекциями двух пересекающихся прямых (рис. 99), г) проекциями двух параллельных прямых (рис. 100).
Рассмотрим некоторые способы графического задания плоскости. Положение плоскости в пространстве может быть определено:
1. тремя точками, не лежащими на одной прямой линии (рис.41)
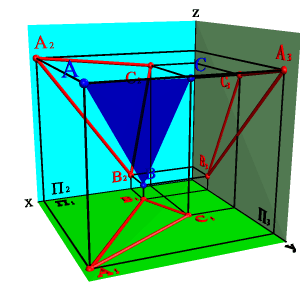
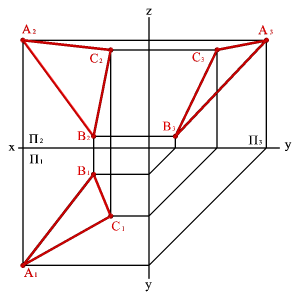
2. прямой линией и точкой, не принадлежащей этой прямой
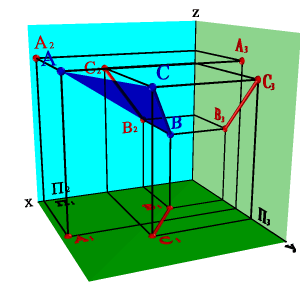
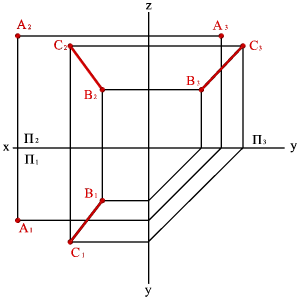
3. двумя пересекающимися прямыми
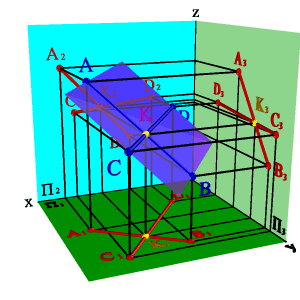
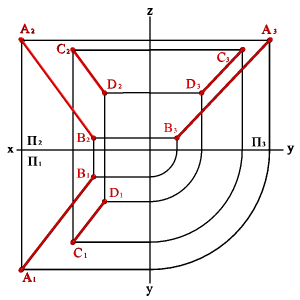
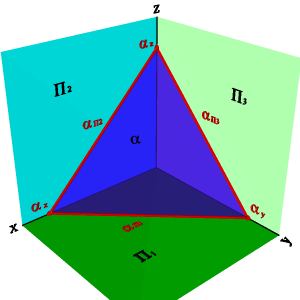
5. О положении плоскости относительно плоскостей проекций удобно судить по её следам (рис.45).
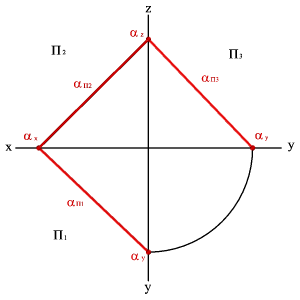
Следом плоскости называется прямая линия, по которой плоскость пересекается с плоскостью проекций. В зависимости от того, какую плоскость проекций пересекает данная плоскость различают горизонтальныйП1, фронтальный П2 и профильный П3 следы
10. Прямая и точка в плоскости. Прямые особого положения.
1) Прямая принадлежит плоскости, если она проходит через две точки, принадлежащие данной плоскости.
2) Прямая принадлежит плоскости, если она проходит через точку, принадлежащую данной плоскости, и параллельна прямой, находящейся в этой плоскости или параллельной ей.
К числу прямых, занимающих особое положение в плоскости, отнесем горизонтали, фронтали ') и линии наибольшего наклона к плоскостям проекций. Линию наибольшего наклона к пл. я, будем называть линией ската плоскости2).
Горизонталями плоскости называются прямые, лежащие в пей и параллельные горизонтальной плоскости проекций.
11. Положение плоскости относительно плоскостей проекций.
В зависимости от положения плоскости по отношению к плоскостям проекций она может занимать как общее, так и частные положения.
1. Плоскость не перпендикулярная ни одной плоскости проекций называется плоскостью общего положения. Такая плоскость пересекает все плоскости проекций (имеет три следа: - горизонтальный П1; - фронтальный П2; - профильный П3).
2. Плоскости, перпендикулярные плоскостям проекций – занимают частное положение в пространстве и называются проецирующими. В зависимости от того, какой плоскости проекций перпендикулярна заданная плоскость, различают:
2.1. Плоскость, перпендикулярная горизонтальной плоскости проекций (П), называется горизонтально проецирующей плоскостью. Горизонтальная проекция такой плоскости представляет собой прямую линию, которая одновременно является её горизонтальным следом. Горизонтальные проекции всех точек этой плоскости совпадают с горизонтальным следом
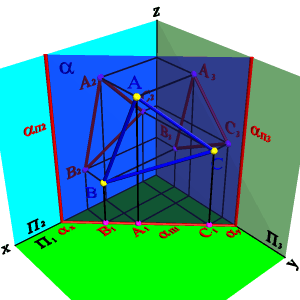
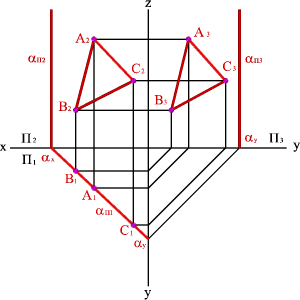
.2. Плоскость, перпендикулярная фронтальной плоскости проекций (П2)- фронтально проецирующая плоскость. Фронтальной проекцией плоскости является прямая линия, совпадающая со следом П2
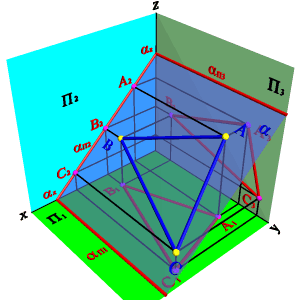
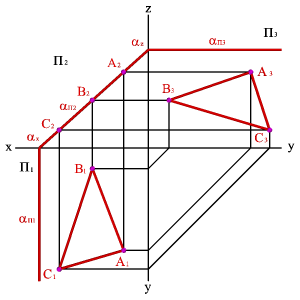
2.3. Плоскость, перпендикулярная профильной плоскости ( П3) - профильно проецирующая плоскость. Частным случаем такой плоскости является биссекторная плоскость (рис.48).