48. Примеры построения разверток поверхностей

7.1. Построение разверток многогранников

Развертка многогранника представляет собой плоскую фигуру, полученную при совмещении всех его граней с плоскостью. Следовательно, построение развертки многогранника сводится к построению истинных величин его граней. Выполнение этой операции связано с определением натуральных величин его ребер, которые являются сторонами многоугольников - граней, а иногда и некоторых других элементов. Ребра многогранника условно разделяются на боковые и стороны основания. Построение развертки пирамиды Боковые грани любой пирамиды являются треугольниками. 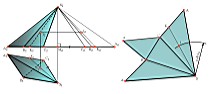Для построения развертки пирамиды (рис. 7.2 ) необходимо предварительно определить натуральные величины боковых ребер и сторон основания.  Р ис. 7.2

У изображенной на рисунке пирамиды стороны основания являются горизонталями и проецируются на плоскость П₁ в истинную величину. Длины боковых ребер определены построением прямоугольных треугольников  S₂M₀C₀, S₂M₀B₀ и S₂M₀А₀, у которых одним катетом является высота пирамиды (S₂М₀ - разность высот точки S и точек А, В, С), а другим - горизонтальная проекция соответствующего ребра.

(/M₀C₀/ = /S₁C₁/; /M₀B₀/ = /S₁B₁/; /M₀A₀/ = /S₁A₁/; /M₀K₀/ = /S₁K₁/).

Натуральные величины ребер пирамиды могут быть определены способом вращения вокруг оси, проходящей через вершину S и перпендикулярной плоскости П₁. Следующая операция состоит в построении каждой боковой грани как треугольника по трем сторонам. В результате получается развертка боковой поверхности пирамиды в виде ряда примыкающих друг к другу треугольников с общей вершиной S. Присоединив к полученной фигуре основание ( АВС), получим полную развертку пирамиды. Построение на развертке точки 1, принадлежащей поверхности пирамиды, понятно из чертежа. На рис. 7.3 показана динамическая схема развертки наклонной пирамиды.

Р ис. 7.3(анимационный)

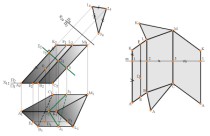
Построение развертки призмы Наклонная призма изображена на рис. 7.4. Призма расположена так, что ее боковые ребра параллельны плоскости П₂ и проецируются на нее в натуральную величину. Стороны оснований являются горизонталями и проецируются на плоскость П₁ без искажения. Таким образом, длины сторон каждой грани известны, однако этого еще недостаточно для построения истинной формы боковых граней.

Р ис. 7.4

Боковые грани наклонной призмы являются параллелограммами, которые не могут быть построены по четырем сторонам. Для построения параллелограмма необходимо помимо длины сторон знать еще его высоту. Для определения высот граней пересечем призму плоскостью  ( ₂), перпендикулярной к ребрам, и определим истинную величину сечения способом замены плоскостей проекций. Стороны этого нормального сечения и будут высотами соответствующих граней. Теперь приступаем к построению развертки. На свободном месте чертежа проводим горизонтальную прямую m и откладываем на ней отрезки /1 - 2/ = /1₄ - 2₄/, /2 - З/ = /2₄ - 3₄/ и /3 - 1/ = /3₄ - 1₄/.

Р ис. 7.5(анимационный)

Через точки 1, 2, 3, 1 проводим перпендикуляры к прямой m и откладываем на них величины боковых ребер так, чтобы /А1/ = /А₂1₂/ и /1К/ = /1₂К₂/, /В2/ = /В₂2₂/ и /2L/ = /2₂L₂/ и т. п.  Соединив концы построенных отрезков, получим развертку боковой поверхности призмы. Присоединив к ней оба основания, получим полную развертку призмы. Построение на развертке точки 4, принадлежащей поверхности призмы, понятно из чертежа. На рис. 7.5 показана динамическая схема развертки поверхности наклонной призмы.