
- •1. Образование проекций. Проекции центральные и параллельные. Понятие однозначности объекта и чертежа. Метод Монжа
- •2. Точка в системе двух и трех плоскостей проекций. Ортогональные проекции и система прямоугольных координат.
- •4. Проекция отрезка прямой линии. Частные положения прямой линии относительно плоскостей проекций.
- •5. Точка на прямой. Следы прямой.
- •7. Взаимное положение двух прямых
- •1. Параллельные прямые линии.
- •2. Пересекающиеся прямые.
- •3. Скрещивающиеся прямые
- •8. Проекциях плоских углов.
- •9. Различные способы задания плоскости на чертеже (включая следы плоскости).
- •10. Прямая и точка в плоскости. Прямые особого положения.
- •11. Положение плоскости относительно плоскостей проекций.
- •12. Плоскости частного положения, их свойства. Использование этих
- •13. Построение проекций плоских фигур. Плоские кривые
- •14. Пересечение прямой линии с проецирующей плоскостью.
- •15 Взаимнопересекающиеся плоскости.
- •17. Пересечение прямой линии с плоскостью общего положения.
- •18. Построение линии пересечения двух плоскостей по точкам пересечения прямых линий с плоскостью
- •31. Вращение вокруг осей, параллельных плоскостям проекций.
- •32. Определение натуральной величины плоской фигуры вращением вокруг фронтами или горизонтали.
- •33. Способ совмещения. Определения натуральной величины плоской фигуры распложенной в плоскости.
- •34. Чертежи призм и пирамид. Пересечение призм плоскостью
- •35. Пересечение пирамиды плоскостью.
- •37. Развертывание поверхностей многогранников.
- •38.Цилиндрические и конические винтовые линии.
- •39. Общие сведенья о кривых поверхностях. Обзор кривых поверхностей, их задание и изображение на чертеже.
- •40. Поверхности вращения.
- •41. Винтовые поверхности и винты
- •42. Проведение плоскостей, касательных к кривым поверхностям.
- •43. Пересечение цилиндрической поверхности плоскостью. Построение развертки
- •45. Пересечение кривых поверхностей с кривой линией
- •46. Построение линии взаимного пересечения поверхностей способом вспомогательных секущих плоскостей.
- •47. Применения вспомогательных секущих сфер при построении линии пересечения поверхностей вращения.
- •48. Примеры построения разверток поверхностей
- •7.1. Построение разверток многогранников
- •7.2. Построение разверток кривых развертывающихся поверхностей
- •7.3. Построение условных разверток неразвертывающихся поверхностей
- •49. Аксонометрические проекции
1. Образование проекций. Проекции центральные и параллельные. Понятие однозначности объекта и чертежа. Метод Монжа
В основу построения объекта на плоскости положен метод проекций. Проецирование – это построение объекта на плоскости при помощи проецирующих лучей, исходящих из точки. Плоскость, на которую падают лучи – проецирующая плоскость.
Виды проецирования
1. Центральное проецирование – проецирующие лучи выходят из одной точки (центра). Размеры предмета на плоскости проекций искажаются (рис.1).
2.
Параллельное проецирование –
проецирующие лечи параллельны и
составляют с плоскостью угол 90%
(прямоугольное
проецирование рис.2)
и угол отличный от 90 % (косоугольное
проецирование рис.3).
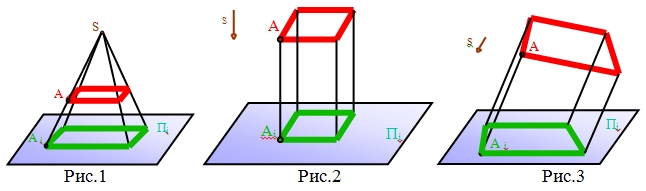
Однозадачность – размеры объекта должны совпадать с размерами на чертеже
Метод монжа
Данный метод позволяет определить место каждой точки изображения относительно других точек.Точку (предмет) помещают в систему двух взаимо перпендикулярных плоскостей, которые используются в качестве плоскостей проекций.
Если даны проекции точки , то можно найти точку, если дана точка, то можно найти проекции.
Две проекции точки вполне определяют ее положение в пространстве относительно данной системы плоскостей проекций.
2. Точка в системе двух и трех плоскостей проекций. Ортогональные проекции и система прямоугольных координат.
ортогональной проекцией точки на плоскость является основание перпендикуляра, опущенного из данной точки на эту плоскость. На рисунке 7 показана точка А и ее ортогональные проекции А1 и А2, которые называют соответственно горизонтальной и фронтальной проекциями.
Проекции
точки всегда расположены на прямой,
перпендикулярной оси x12 и
пересекающей эту ось в точке А x.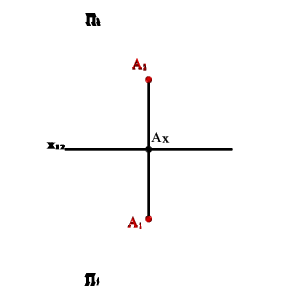
Помимо двух плоскостей вводят еще 3 – профильную, и точка уже имеет координаты
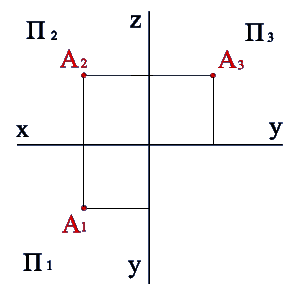 .
.
Координаты -числа, заданием которых определяется положение точки на плоскости, на поверхности или в пространстве. Взаимно перпендикулярные оси представляют прямоугольную систему координат, отличающуюся от декартовой системы координат, применяемой в математике, направлением осей.
3. Точка в четвертях и октантах пространства.
Плоскости
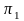 и
и
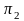 при пересечении образуют четыре
двухгранных
угла.
Их называют квадрантами
или четвертями.
Принятый порядок отсчета плоскостей и
примеры расположения точек приведены
на рисунке 1.17, где номера четвертей
отмечены римскими цифрами. Следует
внимательно изучить второе изображение
этого рисунка, так как это даст возможность
быстро и безошибочно отмечать
принадлежность точки соответствующей
четверти.Обычно считают, что зритель
всегда находится в первой четверти на
большом расстоянии и плоскости проекций
не прозрачны, поэтому видимы только
точки, расположенные в первой четверти,
а также на полуплоскостях
и
.
при пересечении образуют четыре
двухгранных
угла.
Их называют квадрантами
или четвертями.
Принятый порядок отсчета плоскостей и
примеры расположения точек приведены
на рисунке 1.17, где номера четвертей
отмечены римскими цифрами. Следует
внимательно изучить второе изображение
этого рисунка, так как это даст возможность
быстро и безошибочно отмечать
принадлежность точки соответствующей
четверти.Обычно считают, что зритель
всегда находится в первой четверти на
большом расстоянии и плоскости проекций
не прозрачны, поэтому видимы только
точки, расположенные в первой четверти,
а также на полуплоскостях
и
.
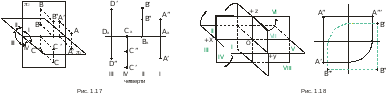
4. Проекция отрезка прямой линии. Частные положения прямой линии относительно плоскостей проекций.
Любой отрезок можно представить как определенную совокупность точек, поэтому, чтобы получить проекцию отрезка АВ на плоскости Н, нужно построить проекции точек А и В, затем соединить их между собой, получив тем самым проекцию отрезка прямой — ab
1. Проекция отрезка прямой, полученная при прямоугольном проецировании на плоскость проекций, не может быть больше самого отрезка. 2. Если отрезок прямой параллелен плоскости проекций, то на нее он спроецируется в натуральную величину. 3. Если отрезок прямой перпендикулярен плоскости проекций, то на нее он спроецируется в точку. 4. Если в пространстве отрезок прямой наклонен к плоскости проекций, он проецируется на нее с искажением (т. е. размер проекции отрезка будет меньше действительного).
1. Прямая не параллельная ни одной плоскости проекций называется прямой общего положения
2. Прямые параллельные плоскостям проекций, занимают частное положение в пространстве и называются прямыми уровня. В зависимости от того, какой плоскости проекций параллельна заданная прямая, различают:
2.1. Прямые параллельные горизонтальной плоскости проекций называются горизонтальными или горизонталями
Прямые параллельные фронтальной плоскости проекций называются фронтальными или фронталями
Прямые параллельные профильной плоскости проекций называются профильными
Различают восходящую и нисходящую профильные прямые. Первая по мере удаления от зрителя поднимается, вторая - понижается.
