
- •1. Решение слпу с трехдиагональной матрицей методом прогонки.
- •2. Решение нелинейного уравнения методом хорд и методом Ньютона.
- •3. Модификации метода Ньютона для решения нелинейного уравнения. Метод секущих для нелинейного уравнения.
- •Метод хорд для нелинейного уравнения.
- •Упрощенный метод Ньютона.
- •Модификация метода Ньютона для системы двух уравнений.
- •4. Определение действительных корней алгебраического уравнения.
- •5. Определение комплексных корней алгебраического уравнения методом Лина.
- •6.Решение системы нелинейных уравнений методом Ньютона.
- •10.Численное решение задачи Коши для обыкновенного дифференциального уравнения методом Милна.
- •11.Численное решение краевой задачи для обыкновенного дифференциального уравнения методом конечных разностей.
- •12. Численное решение краевой задачи для обыкновенного дифференциального уравнения методом прогонки.
- •13. Численное решение задачи Дирихле для уравнения Лапласа методом сеток.
- •14. Численное решение смешанной задачи для дифференциального уравнения параболического типа методом сеток.
- •15. Численное решение смешанной задачи для дифференциального уравнения гиперболического типа методом сеток.
- •16. Задачи оптимизации. Основные понятия (проектные параметры, целевая функция). Постановка задачи. Основные типы задач оптимизации.
- •17. Одномерная задача оптимизации. Аналитическое решение и решение методом золотого сечения.
- •18. Одномерная задача оптимизации. Решение и решение методом Фибоначчи.
- •Одномерная задача оптимизации. Решение методом Пауэлла
- •Метод пауэлла
- •21.Многомерная задача оптимизации. Аналитическое решение и решение методом покоординатного спуска.
- •Метод покоординатного спуска
- •22.Многомерная задача оптимизации. Решение методом градиентного спуска.
- •Метод градиентного спуска
- •23. Многомерная задача оптимизации. Решение методом наискорейшего спуска.
- •Метод наискорейшего спуска
- •24.Задачи математического программирования. Решение методом штрафных функций.
- •25. Линейное программирование. Постановка задачи. Решение геометрическим методом.
- •26. Линейное программирование. Решение задачи симплекс-методом.
- •27.Линейное программирование. Решение задачи методом потенциалов.
- •28. Решение интегрального уравнения методом замены ядра уравнения на вырожденное.
- •29. Решение интегрального уравнения Фредгольма II рода методом Крылова-Боголюбова.
- •30. Решение интегрального уравнения Фредгольма II рода методом Бубнова-Галеркина.
- •Основа метода
- •31.Решение интегрального уравнения Фредгольма I рода методом регуляризации Тихонова.
- •Метод регуляризации Тихонова
15. Численное решение смешанной задачи для дифференциального уравнения гиперболического типа методом сеток.
Рассмотрим
смешанную задачу для уравнения колебания
струны, заключающуюся в отыскании
функции, удовлетворяющей уравнению
 ,а также начальным условиям
,а также начальным условиям
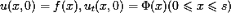 и
краевым условиям
и
краевым условиям
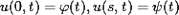
Так как введение переменной τ = at приводит уравнение к виду
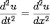 ,
то в дальнейшем можно принять a=1.
,
то в дальнейшем можно принять a=1.
Построив в полуполосе два семейства параллельных прямых x = ih(i = 0,1,2,...,n),t = jl(j = 0,1,2,...),
заменяем производные в уравнении разностными отношениями.
Пользуясь
симметричными формулами для производных,
будем иметь

Обозначив α = l / h, получим разностное уравнение
ui,j + 1 = 2ui,j− ui,j− 1 + α2(ui,j+ 1 − 2ui,j+ ui,j − 1).
Доказано, что при α>=0 это разностное уравнение устойчиво.
В частности, при α = 1 уравнение имеет наиболее наиболее простой вид: ui,j + 1 = ui + 1,j+ ui − 1,j− ui,j − 1.
Оценка
погрешности приближенного решения,
полученного из уравнения в полосе
![]() ,
имеет вид
,
имеет вид
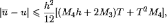
где
 -точное
решение ,
-точное
решение ,
16. Задачи оптимизации. Основные понятия (проектные параметры, целевая функция). Постановка задачи. Основные типы задач оптимизации.
Под оптимизацией понимают процесс выбора наилучшего варианта из всех возможных.
В процессе решения задачи оптимизации обычно необходимо найти оптимальные значения некоторых параметров, определяющих данную задачу. При решении инженерных задач их принято называть проектными параметрами. В качестве проектных параметров могут быть, в частности, значения линейных размеров объекта, массы, температуры и т.п.
Выбор оптимального решения или сравнение двух альтернативных решений проводится с помощью некоторой зависимой величины (функции), определяемой проектными параметрами. Эта величина называется целевой функцией (или критерием качества).
Задачи оптимизации
Можно выделить два типа задач оптимизации - безусловные и условные. Безусловная задача оптимизации состоит в отыскании максимума или минимума действительной функции (1) от п действительных переменных и определения соответствующих значений аргументов на некотором множестве п-мерного пространства.
Условныезадачи оптимизации, или задачи с ограничениями, - это такие, при формулировке которых задаются некоторые условия (ограничения) на множестве .
Ограничения-равенства выражают зависимость между проектными параметрами, которая должна учитываться при нахождении решения.
В результате ограничений область проектирования , определяемая всеми п проектными параметрами, может быть существенно уменьшена в соответствии с физической сущностью задачи. Число т ограничений-равенств может быть произвольным. Их можно записать в виде
 (2)
(2)
В ряде случаев из этих соотношений можно выразить одни проектные параметры через другие. Это позволяет исключить некоторые параметры из процесса оптимизации, что приводит к уменьшению размерности задачи и облегчает ее решение. Аналогично могут вводиться также ограничения-неравенства, имеющие вид
 (3)
(3)
Следует отметить особенность в отыскании решения при наличии ограничений. Оптимальное решение здесь может соответствовать либо локальному экстремуму (максимуму или минимуму) внутри области проектирования, либо значению целевой функции на границе области. Если же ограничения отсутствуют, то ищется оптимальное решение на всей области проектирования, т.е. глобальный экстремум.
Теория и методы решения задач оптимизации при наличии ограничений составляют предмет исследования одного из важных разделов прикладной математики - математического программирования.
Пример постановки задачи
Пусть требуется спроектировать контейнер в форме прямоугольного параллелепипеда объемом V = 1 м3, причем желательно израсходовать на его изготовление как можно меньше материала.
При постоянной толщине стенок последнее условие означает, что площадь полной поверхности контейнера S должна быть минимальной. Если обозначить через x1, x2, x3 длины ребер контейнера, то задача сведется к минимизации функции
 .
(4)
.
(4)
Эта функция в данном случае является целевой, а условие V= 1 - ограничением-равенством, которое позволяет исключить один параметр:
 (5)
(5)
Задача свелась к минимизации функции двух переменных. В результате решения задачи будут найдены значения проектных параметров x1, x2а затем иx3. В приведенном примере фактически получилась задача безусловной оптимизации для целевой функции (5), поскольку ограничение-равенство было использовано для исключения параметра x3.
