13. Численное решение задачи Дирихле для уравнения Лапласа методом сеток.

Идея метода конечных разностей (метода сеток) известна давно, с соответствующих трудов Эйлера. Однако практическое применение этого метода было тогда весьма ограничено из-за огромного объема ручных вычислений, связанных с размерностью получаемых систем алгебраических уравнений, на решение которых требовались годы. В настоящее время, с появлением быстродействующих компьютеров, ситуация в корне изменилась. Этот метод стал удобен для практического использования и является одним из наиболее эффективных при решении различных задач математической физики.

Основная идея метода конечных разностей (метода сеток) для приближенного численного решения краевой задачи для двумерного дифференциального уравнения в частных производных состоит в том, что

1) на плоскости в области А, в которой ищется решение, строится сеточная область Аs (рис.1), состоящая из одинаковых ячеек размером s ( s – шаг сетки) и являющаяся приближением данной области А;

2) заданное дифференциальное уравнение в частных производных заменяется в узлах сетки Аs соответствующим конечно-разностным уравнением;

3) с учетом граничных условий устанавливаются значения искомого решения в граничных узлах области Аs .

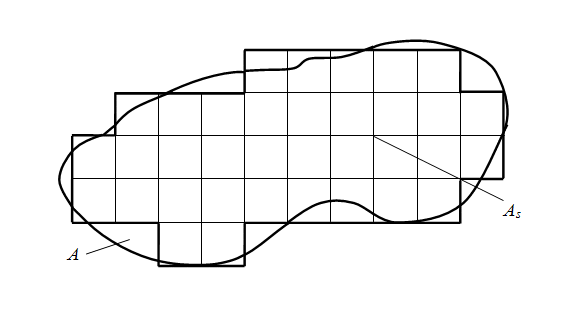
Рис. 1. Построение сеточной области

Решая полученную систему конечно-разностных алгебраических уравнений, получим значения искомой функции в узлах сетки Аs , т.е. приближенное численное решение краевой задачи. Выбор сеточной области Аs зависит от конкретной задачи, но всегда надо стремиться к тому, чтобы контур сеточной области Аs наилучшим образом аппроксимировал контур области А.

Рассмотрим уравнение Лапласа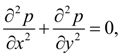 (1)

где p ( x, y ) – искомая функция, x, y – прямоугольные координаты плоской области и получим соответствующее ему конечно-разностное уравнение.

Заменим частные производные и в уравнении (1) конечно-разностными отношениями:

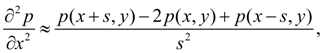
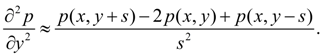
Тогда решая уравнение (1) относительно p ( x, y ), получим:

(2)

Задав значения функции p ( x, y ) в граничных узлах контура сеточной области Аs в соответствии с граничными условиями и решая полученную систему уравнений (2) для каждого узла сетки, получим численное решение краевой задачи (1) в заданной области А.

Ясно, что число уравнений вида (2) равно количеству узлов сеточной области Аs, и чем больше узлов (т.е. чем мельче сетка), тем меньше погрешность вычислений. Однако надо помнить, что с уменьшением шага s возрастает размерность системы уравнений и следовательно, время решения. Поэтому сначала рекомендуется выполнить пробные вычисления с достаточно крупным шагом s , оценить полученную погрешность вычислений, и лишь затем перейти к более мелкой сетке во всей области или в какой-то ее части.

14. Численное решение смешанной задачи для дифференциального уравнения параболического типа методом сеток.

Рассмотрим смешанную задачу для уравнения теплопроводности, а именно найти функцию u(x,t), удовлетворяющую уравнению

(*),

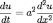начальному условию u(x,0) = f(x)(0 < x < s)

и краевым условиям .

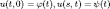Рассмотрим задачу о распространение тепла в однородном стержне длины s. Путем введем новой переменной τ = a2t уравнение (*) приводится к виду

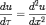, поэтому в дальнейшем примем a = 1.

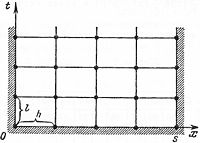
Построим в полуполосе (см рис) два семейства параллельных прямых:

x = ih(i = 0,1,2,...),t = jl(j = 0,1,2,...).

Обозначим x_i = ih,t_j = jl,u(x_i,t_j) = u_ij и приближенно заменим в каждом внутреннем узле (x_i,t_j) производную 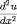разностным отношением

а производнуюdu/dt одним из двух разностных отношений

Тогда для уравнения (*) при a=1 получаем два типа конечно-разностных уравнений:

(^)

(^^)

Обозначив σ = l / h2 , приводим уравнения к виду

u_{i,j + 1} = (1 − 2σ)u_ij + σ(u_{i+ 1},_j + u_{i − 1,j}), (#)

(1 + 2σ)u_ij − σ(u_{i + 1,j} + u_{i − 1,j}) − u_i,j− 1 = 0 (##).

Отметим, что для составления уравнения (^)была использована схема узлов, данная на рисунке 18-явная схема, для уравнения (^^)-схема узлов, данная на рисунке 19-неявная схема.

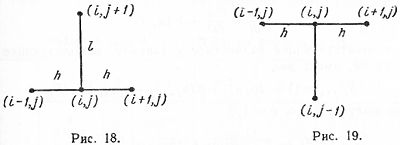
При выборе σ в уравнениях следует учитывать два обстоятельства:

1)погрешность замены дифференциального уравнения разностным должна быть наименьшей;

2)разностное уравнение должно быть устойчивым.

Доказано, что уравнение (#) будет устойчиво при ,а уравнение (##) -при любом σ. Наиболее удобный вид уравнение (#) имеет при σ = 1 / 2:

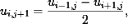и при σ = 1 / 6: