Модификация метода Ньютона для системы двух уравнений.

Для решения системы из двух уравнений

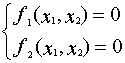
используется следующая модификация метода Ньютона: (2.22)

где (x1(0), x2(0)) - некоторое начальное приближение к искомому корню.

ЗАМЕЧАНИЕ 2.7 1) В данном методе в отличие от классического метода Ньютона обратную матрицу требуется подсчитывать только один раз.

2) Условие окончания итерационного процесса имеет вид: || x(k+1) - x(k) || ≤ ε

4. Определение действительных корней алгебраического уравнения.

Пусть дано алгебраическое уравнение (2.1) или в развёрнутом виде (2.2) с действительными коэффициентами a0…an.В высшей алгебре доказывается ряд утверждений, позволяющих найти границы расположения корней уравнения (2.2) в комплексной области и отделить действительные корни.

Приведём без доказательства некоторые теоремы, позволяющие установить границы расположения корней уравнения (2.2)

Теорема 1. Если ,то все корни уравнения (2.2) расположены в кольце:

Теорема 2. Если a – максимум модулей отрицательных коэффициентов уравнения, a0>0 и первый отрицательный коэффициент в последовательности a1 a2 ..an есть am , то все положительные корни уравнения меньше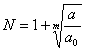 (если отрицательных коэффициентов нет, то нет и положительных корней).

Теорема 3. Если a0>0 и при x=c>0 имеют место неравенства то число c служит верхней границей положительных корней уравнения (2.2).

Теорема 4.Пустьзаданымногочлены

и – верхние границы положительных корней соответственно многочленов Тогда все положительные корни уравнения (2.2) лежат на отрезке , а все отрицательные корни – на отрезке . Теоремы ниже, дают возможность определить число действительных корней уравнения .

Теорема 5. (теорема Декарта). Число положительных корней уравнения (2.2) с учётом их кратности равно числу перемен знаков в последовательности а0a1 a2 ..anкоэффициентов или меньше этого числа на чётное число.

Заметим, что для определения количества отрицательных корней достаточно применить теорему Декарта к многочленуf(-x) .

Отметим, что теорема Декарта, так же как и теорема Бюдана-Фурье, не требует больших вычислений, но не всегда даёт точное количество действительных корней уравнения (2.2). Если уравнение (2.2) не имеет кратных корней на[α,β] , то точное число действительных корней уравнения (2.2) на отрезке [α,β] даёт теорема Штурма.

Прежде чем её сформулировать, введём обозначения, предположив, что уравнение (2.2) не имеет кратных корней. Обозначим через f₁(x) производнуюf’₍x) ; черезf₂(x) остаток от деленияf₍x)наf₁(x), взятый с обратным знаком; черезf₃(x)остатокот деленияf₁(x)наf₂(x) , взятый с обратным знаком, и так далее, до тех пор, пока не придём к постоянной. Полученную последовательность (2.5) назовём рядом Штурма.

Теорема 6 (теорема Штурма). Число действительных корней уравненияf(x)=0 , расположенных на отрезке[α,β] , равно разности между числом перемен знаков в последовательности (2.5) при x=α и числом перемен знаков в последовательности (2.5) приx=β.

Заметим, что использование теоремы Штурма на практике связано с большой вычислительной работой при построении ряда Штурма.