29. Решение интегрального уравнения Фредгольма II рода методом Крылова-Боголюбова.

Интегральным уравнением называется такое уравнение, неизвестная функция в котором содержится под знаком интеграла. В общем случае интегральное уравнение имеет вид

Уравнение Фредгольма второго рода имеет вид

МЕТОД УСРЕДНЕНИЯ- метод, применяемый в теории нелинейных колебаний для исследования колебательных процессов, основанный на принципе усреднения (осреднения), заменяющем точное дифференциальноеуравнение движения усредненным.

Применяются для изучения нелинейных колебаний.Система уравнений, для которых разработанметодусреднения Крылова - Боголюбова, имеет стандартный вид:

где t - время, е - малый положительный параметр. Основные предположения, при которых рассматривается система (1), сводятся к достаточной гладкости функции Xпо l, x и некоторой"возвращаемости" ее по t, обеспечивающей существование среднего значения 

например, периодичности или почти периодичности Xпо t. Согласнометоду усреднения Крылова – Боголюбова т-е приближение к решению x=x(t)системы (1) определяется выражением 

в котором   - решение "усредненного" уравнения 

 - функции, подбираемые из условия, чтобы выражение (2) удовлетворяло уравнению (1) с точностью до величин порядка   и чтобы F_j обладали по tтой же возвращаемостью, что и правая часть системы (1). Функции F_j находятся элементарно, функции Р _j определяются в результате усреднения правой части системы (1) после подстановки в нее выражения (2). Так, в частности, для системы (1) с периодической по tправой частью, когда 

функция F₁ определяется по (3) согласно формуле 

функции F_m и Р _m при   определяются по соотношению 

аналогичными формулами. Обоснование метода усреднения сводится к следующему:

1) установление оценки: 

где   при   - постоянная, не зависящая от   

2) доказательство существования решения x=x₀(t) системы (1), находящегося в достаточно малой окрестности положения равновесия  усредненной системы:

и установление свойств устойчивости, периодичности или почти периодичности этого решения;

3) доказательство существования интегрального многообразия t:

системы (1), находящегося вблизи периодической траектории   усредненной системы:

и исследование поведения решении системы (1), начинающихся в окрестности многообразия т.

30. Решение интегрального уравнения Фредгольма II рода методом Бубнова-Галеркина.

Метод Галёркина (метод Бубнова — Галёркина) — метод приближённого решения краевой задачи для дифференциального уравнения

Основа метода

Первым шагом в реализации метода Галёркина является выбор набора базисных функций, которые:

• удовлетворяют граничным условиям.

• в пределе бесконечного количества элементов базиса образуют полную систему.

Решение представляется в виде разложения по базису:

Затем приближённое решение подставляется в исходное дифференциальное уравнение, и вычисляется его невязка. Для однородного уравнения:

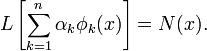
Для неоднородного уравнения L[u]=f(x) невязка будет иметь вид N(x)=L[u]-f(x)

Далее выдвигается требование ортогональности невязки к базисным функциям, то есть:

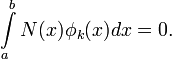
Отсюда получается однородная система уравнений для коэффициентов в разложении, и удаётся приближённо найти собственные значения задачи.