23. Многомерная задача оптимизации. Решение методом наискорейшего спуска.

Минимум функции нескольких переменных. В одномерных задачах оптимизации целевая функция зависит лишь от одного аргумента. Однако в большинстве реальных задач оптимизации, представляющих практический интерес, целевая функция зависит от многих проектных параметров.

Минимум дифференцируемой функции многих переменных u= f(x₁,x₂,…,x_n) можно найти, исследуя ее значения в критических точках, которые определяются из решения системы дифференциальных уравнений

.

Метод наискорейшего спуска

Выбирают , где все производные вычисляются при , и уменьшают длину шага по мере приближения к минимуму функцииF .

Для аналитических функций F иf_iмалых значений тейлоровское разложение позволяет выбрать оптимальную величину шага

(5)

где все производные вычисляются при . Параболическая интерполяция функции может оказаться более удобной .

Алгоритм

1. Задаются начальное приближение и точность расчёта

2. Рассчитывают , где

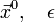
3. Проверяют условие останова:

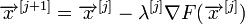
• Если 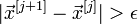, то и переход к шагу 2.

• Иначе 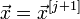и останов.

24.Задачи математического программирования. Решение методом штрафных функций.

Метод штрафных функций. Решение задач математического программирования значительно более трудоемко по сравнению с задачами безусловной оптимизации. Ограничения типа равенств или неравенств требуют их учета на каждом шаге оптимизации. Одним из направлений в методах решения задач математического программирования является сведение их к последовательности задач безусловной оптимизации. К этому направлению относится, в частности, метод штрафных функций.

Сущность метода состоит в следующем. Пусть f(x₁,x₂,…,x_n) - целевая функция, для которой нужно найти минимум т в ограниченной области D( ). Данную задачу заменяем задачей о безусловной минимизации однопараметрического семейства функций

. (2)

При этом дополнительную (штрафную) функцию (x) выберем таким образом, чтобы при решение вспомогательной задачи стремилось к решению исходной или, по крайней мере, чтобы их минимумы совпадали: при .

Штрафная функция (x) должна учитывать ограничения, которые задаются при постановке задачи оптимизации. В частности, если имеются ограничения-неравенства вида (j = 1,2,…, J), то в качестве штрафной функции можно взять функцию, которая: 1) равна нулю во всех точках пространства проектирования, удовлетворяющих заданным ограничениям-неравенствам; 2) стремится к бесконечности в тех точках, в которых эти неравенства не выполняются. Таким образом, при выполнении ограничений-неравенств функции f(x) и F(x,) имеют один и тот же минимум. Если хотя бы одно неравенство не выполнится, то вспомогательная целевая функция F(x,) получает бесконечно большие добавки. И ее значения далеки от минимума функции f(x). Другими словами, при несоблюдении ограничений-неравенств налагается «штраф». Отсюда и термин «метод штрафных функций».

Теперь рассмотрим случай, когда в задаче оптимизации заданы ограничения двух типов - равенства и неравенства:

(3)

В этом случае в качестве вспомогательной целевой функции, для которой формулируется задача безусловной оптимизации во всем п-мерном пространстве, принимают функцию

. (4)

Здесь взята такая штрафная функция, что при выполнении условий (3) она обращается в нуль. Если же эти условия нарушены (т. е. , h_j(x) < 0 и signh_j(x) = -1), то штрафная функция положительна. Она увеличивает целевую функцию f(x) тем больше, чем больше нарушаются условия (3).

При малых значениях параметра  вне области D функция F(x,) сильно возрастает. Поэтому ее минимум может быть либо внутри D, либо снаружи вблизи границ этой области. В первом случае минимумы функций F(x,) и f(x) совпадают, поскольку дополнительные члены в (4) равны нулю. Если минимум функции F(x,) находится вне D, то минимум целевой функции f(x) лежит на границе D. Можно при этом построить последовательность такую, что соответствующая последовательность минимумов функции F(x,) будет стремиться к минимуму функции f(x).

Таким образом, задача оптимизации для целевой функции f(x) с ограничениями (3) свелась к последовательности задач безусловной оптимизации для вспомогательной функции (4), решение которых может быть проведено с помощью методов спуска. При этом строится итерационный процесс при  0.