21.Многомерная задача оптимизации. Аналитическое решение и решение методом покоординатного спуска.

Минимум функции нескольких переменных. В одномерных задачах оптимизации целевая функция зависит лишь от одного аргумента. Однако в большинстве реальных задач оптимизации, представляющих практический интерес, целевая функция зависит от многих проектных параметров.

Минимум дифференцируемой функции многих переменных u= f(x₁,x₂,…,x_n) можно найти, исследуя ее значения в критических точках, которые определяются из решения системы дифференциальных уравнений

.

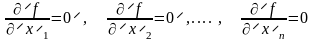Пример. При определении оптимальных размеров контейнера объемом 1 м³ задача свелась к минимизации его полной поверхности, которая в данном случае является целевой функцией

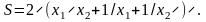
Решение. В соответствии с (1) получим систему

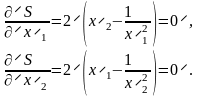
Отсюда находим x₁ =x₂ = 1 м, x₃ = 1/(x₁x₂) = 1 м. Таким образом, оптимальной формой контейнера в данном случае является куб, длина ребра которого равна 1 м.

Метод покоординатного спуска

Пусть требуется найти наименьшее значение целевой функции u= f(x₁,x₂,…,x_n). В качестве начального приближения выберем в п-мерном пространстве некоторую точку M₀ с координатами 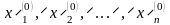. Зафиксируем все координаты функции и, кроме первой. Тогда - функция одной переменной x₁. Решая одномерную задачу оптимизации для этой функции, мы от точки M₀ перейдем к точке 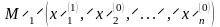, в которой функция и принимает наименьшее значение по координате x₁ при фиксированных остальных координатах. В этом состоит первый шаг процесса оптимизации, состоящий в спуске по координате x₁.

Зафиксируем теперь все координаты, кроме x₂, и рассмотрим функцию этой переменной 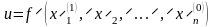. Снова решая одномерную задачу оптимизации, находим ее наименьшее значение при 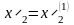, т.е. в точке 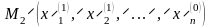. Аналогично проводится спуск по координатамx₃,x₄,…,x_n, а затем процедура снова повторяется от x₁ до x_n и т.д. В результате этого процесса получается последовательность точек M₀,M₁,…, в которых значения целевой функции составляют монотонно убывающую последовательность . 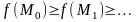На любом k-м шаге этот процесс можно прервать, и значение f(M_k) принимается в качестве наименьшего значения целевой функции в рассматриваемой области.

Данный метод легко проиллюстрировать геометрически для случая функции двух переменныхz=f(x,y), описывающей некоторую поверхность в трехмерном пространстве. На рис. 1 нанесены линии уровня этой поверхности. Процесс оптимизации в этом случае проходит следующим образом. Точка M₀(x₀,y₀) описывает начальное приближение. Проводя спуск по координате х, попадем в точку M₁(x₁,y₀). Далее, двигаясь параллельно оси ординат, придем в точку M₂(x₁,y₁) и т.д.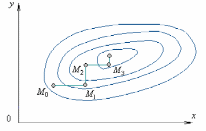

Для функции двух переменных очевидно, что метод неприменим в случае наличия изломов в линиях уровня. Это соответствует так называемому оврагу на поверхности. Здесь возможен случай, когда спуск по одной координате приводит на «дно» оврага. Тогда любое движение вдоль любой координаты ведет к возрастанию функции, соответствующему подъему на «берег» оврага. Поскольку поверхности типа «оврага» встречаются в инженерной практике, то при использовании метода покоординатного спуска следует убедиться, что решаемая задача не имеет этого недостатка. Для гладких функций при удачно выбранном начальном приближении (в некоторой окрестности минимума) процесс сходится к минимуму.