1. Решение слпу с трехдиагональной матрицей методом прогонки.

Трёхдиагональной матрицей или матрицей Якоби называют матрицу следующего вида:

СЛАУ с такими матрицами встречаются при решении многих задач математики и физики. Краевые условия x1 и x_n , которые берутся из контекста задачи, задают первую и последнюю строки. Так краевое условие первого родаF(x=x1)=F1определит первую строку в виде C1=1 B1=0,а условие второго родаdF/dx(x=x1)=F1будет сооn/ значениямC1=-1 B1=1

Метод прогонки используется для решения систем линейных уравнений вида: Ax=F,A -трёхдиагональная матрица. Описание метода

Система уравненийAx=Fравносильна соотношению: Метод прогонки основывается на предположении, что искомые неизвестные связаны рекуррентным соотношением: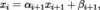 где i=n-1,n-2,…1 (1)

Используя это соотношение, выразим xi-1 и xi через xi+1 и подставим в ур. (1):

где Fi — правая часть i-го уравнения.

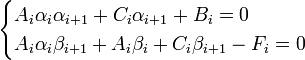Отсюда следует:

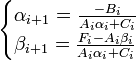Из первого ур. получим: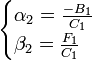

После нахождения прогоночных коэффициентов α и β, используя ур (2), получим решение системы. При этом, i=n-1…1

Другим способом объяснения существа метода прогонки, более близким к терминологии конечно-разностных методов и объясняющим происхождение его названия, является следующий: преобразуем уравнение (1) к эквивалентному ему уравнению: A’x=F’(1’)c надиагональной матрицей:

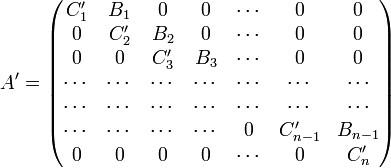Вычисления проводятся в два этапа. На первом этапе вычисляются компоненты матрицыС’_iи вектора F’ начиная с i=2 до i=n: С’_i=C1 и F’₁=F1

На втором этапе, для i=n,n-1,…1 вычисляется решение:

2. Решение нелинейного уравнения методом хорд и методом Ньютона.

Метод хорд — итерационный численный метод приближённого нахождения корня уравнения. Описание метода:

Пусть x1, x2 –абсциссы концов хорды, y=kx+b– ур.прямой, содержащей хорду. Найдем k и bиз системы: Вычтем из первого уравнения второе: , затем найдем k и b

Уравнение принимает вид: Таким образом, теперь можем найти первое приближение к корню, полученное методом хорд: Теперь возьмем координатыx2 и x3 и повторим все проделанные операции, найдя новое приближение к корню. Повторять операцию следует до тех пор, пока |x_n-x_n-1| не станет меньше или равно заданному значению погрешности.

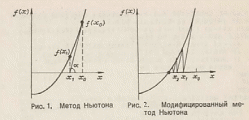
Метода Ньютона (рис. 1). Предположим, что графическим методом определено начальное приближение х0 к корню. В точке х0 вычислим левую часть решаемого уравнения f0 = f(x0), а также производную в этой точке f'(x0) = tg α. Следующее приближение к корню найдем в точке х1, где касательная к функции f(x), проведенная из точки (х0, f0), пересекает ось абсцисс. Затем считаем точку х1 в качестве начальной и продолжаем итерационный процесс. Из рис. видно, что таким способом можно приближаться к корню х*. При этом с каждой итерацией расстояние между очередным хk+1 и предыдущим хk приближениями к корню будет уменьшаться. Процесс уточнения корня закончим, когда выполнится условие

|xk + 1- xk|< e,

где е - допустимая погрешность определения корня.

Из геометрических соотношений (рис. 1) получим основную формулу метода Ньютона

x1 = x0 - f(x0)/f'(x0)

В общем виде для к-го шага итерационного процесса последнее соотношение принимает вид

xk+1 = xk - f(xk)/f'(xk)

Алгоритм Ньютона можно получить другим способом с помощью разложения в ряд Тейлора левой части уравнения f(x) вблизи корня х*. Пусть xk+1=xk+ s, тогда

f(xk+1)= f(xk)+sf'(xk) + ...,

s ~= -f(xk)/f'(xk),

так как f(xk+1)=> 0 (стремится к нулю).

Метод Ньютона обладает высокой скоростью сходимости. Обычно абсолютная точность решения 10-5 - 10-6 достигается через 5-6 итераций.

Недостатком метода является необходимость вычисления на каждой итерации не только левой части уравнения, но и её производной.

Можно, несколько уменьшив скорость сходимости, ограничиться вычислением производной f'(x) только на первой итерации, а затем вычислять лишь значения f(x), не изменяя производной f'(x). Это алгоритм так называемого модифицированного метода Ньютона (рис. 2).

xk+1 = xk - f(xk)/f'(x0)