34. Формула Гаусса-Остроградського.
Формула Гаусса-Остроградського встановлює зв'язок поверхневого інтегралу ІІ роду по замкненій поверхні з потрійним інтегралом по просторовій області, яка обмежена цією поверхнею.
Теорема.
Нехай
– обмежена область, межа якої
– кусково-гладка поверхня, орієнтована
зовнішніми нормалями. В області
задано неперервно диференційовне поле
.
Тоді потік векторного поля
через межу області
дорівнює потрійному інтегралу від
по області
, тобто
(1) або
(2). Формулу (1) або (2) називають формулою
Гаусса-Остроградського; відповідно у
векторній формі (1) і координатній (2).
○ Розглянемо
область
,
яка є правильною (елементарною) відносно
осі
і обмежена поверхнями
,
.
Область
проектується на площину
в правильну область
,
в якій функції
,
є неперервними. Поверхня
є об’єднанням поверхонь
.
При заданих умовах існує потрійний
інтеграл
і його можна записати у вигляді повторного
інтеграла:
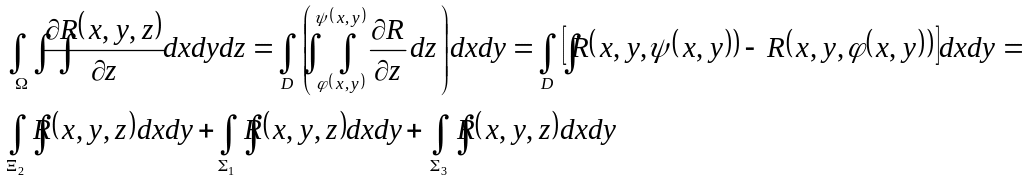(3)
В цій
формулі дописали третій доданок, оскільки
.
Рівність (3) можна записати так:
(4). Можна показати, що формула (4) є
правильною для області, обмеженої
довільними кусково-гладкими поверхнями
(розбиваючи їх на елементарні частини).
Аналогічно можна отримати рівності
(5), де область
– правильна відносно осі
;
(6), де
– правильна область відносно осі
.
Тепер, нехай область
є правильною відносно трьох осей
одночасно. Тоді, додавши відповідно
праві і ліві частини рівностей (4), (5),
(6) отримаємо формулу Гаусса-Остроградського
(2). ●
Зауваження.
Якщо покласти
,
то за формулою (2) можна обчислити об’єм
області
:
,
де
– поверхня, що обмежує область
.
Якщо
,
то
.
Якщо
,
то
.
Якщо
,
то об’єм області
,
обмежений поверхнею
можна обчислити за формулою:
.