Теорема про неперервність інтеграла, залежного від параметра.
Теорема 2.
Якщо
функція
визначена і неперервна як функція від
двох змінних в прямокутнику
,
то інтеграл
є неперервною функцією від параметра
.
○ За
теоремою Кантора функція
,
неперервна на компакті, є рівномірно
неперервною на цьому компакті, тобто
для
,
що із нерівностей
,
слідує
нерівність
.
Покладемо
,
.
Тоді при
для будь-якого
маємо
,
а це означає,
що при
(прямує)
рівномірно відносно
.
Відповідно за теоремою 1 отримуємо
,
тобто
, а це означає, що функція
є неперервною на відрізку
,
оскільки
– довільна точка цього проміжку. ●
Оскільки функція є неперервною на проміжку , то ця функція є інтегрованою на .
Теорема 2.
Якщо
функція
є неперервною в прямокутнику
,
то
.
○ Кожен з повторних інтегралів у цій формулі дорівнює подвійному інтегралу від функції на прямокутнику П.●
32. Диференціювання по параметру інтеграла, межі якого залежать від параметра.
Розглянемо
інтеграл
(1).
Теорема 5.
Нехай
функція
визначена
і неперервна в області
,
де
,
– неперервні функції. Тоді інтеграл
(1) є неперервною функцією від
на
проміжку
.
○ Інтеграл
(1) можна записати у вигляді
(2).
Перший
інтеграл, в якого межі сталі, при
прямує
до інтеграла
за теоремою 2. Два інші інтеграли (2)
допускають оцінки
,
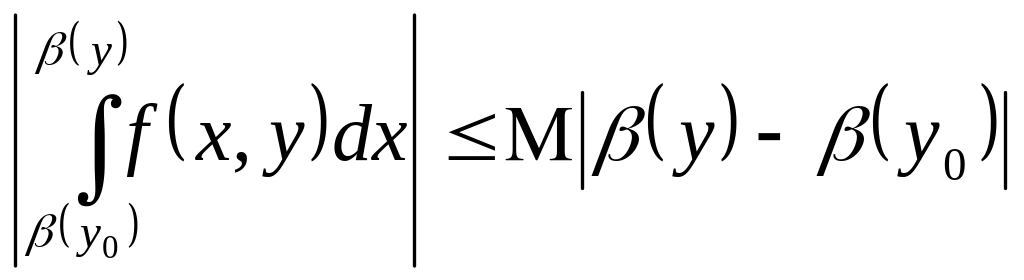(3), де
.
В силу неперервності функцій
,
при
інтеграли (3) прямують до нуля. Отже,
●
Теорема 6.
Якщо
при умовах теореми 5 функція
має неперервну похідну
,
також існують похідні
,
,
то інтеграл (1) має похідну по параметру,
яка обчислюється за формулою:
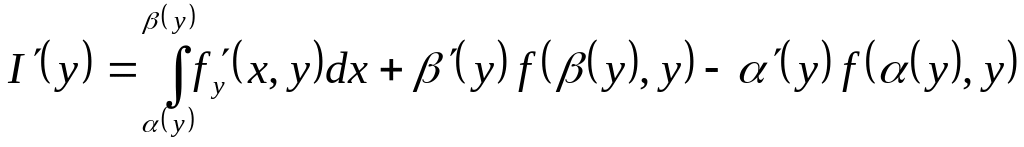(4).
○ Використаємо
рівність (2). За теоремою 4 перший інтеграл
в точці
має похідну
(5).
Для другого інтеграла рівності (2)
значення якого при
є нуль, за теоремою про середнє отримаємо
,
де
міститься між
і
.
Звідси похідна другого інтеграла при
дорівнює
(6). Аналогічно для похідної третього
інтеграла рівності (2)отримаємо вираз
(7). Сумуючи вирази (5), (6), (7) отримаємо
формулу (4). ●
33. Формула Стокса.
Формула
Стокса встановлює
зв'язок між поверхневим інтегралом і
криволінійним інтегралом ІІ роду по
кривій, що оточує цю поверхню. Нехай
задана гладка поверхня
.
Позначимо символом
межу цієї поверхні. Виберемо додатну
орієнтацію поверхні, тобто якщо дивитися
з кінця нормалі, то обхід вздовж кривої
відбувається проти годинникової стрілки.
Нормаль
з віссю
в кожній точці поверхні утворює гострий
кут. Нехай
– рівняння простої поверхні
,
і на цій поверхні задана неперервно
диференційовна функція
.
Оскільки
і координати контура
задовольняють
рівняння
,
то значення функції
на контурі
дорівнюють
значенням функції
на контурі
– проекції на площину
контура
.
Отже,
(1). До правої частини рівності
(1) застосуємо формулу Гріна:
(2). За формулою диференціювання складної
функції отримаємо:
(3). Підставимо праву частину рівності
(3) в формулу (2). Тоді
(4). Врахувавши, що
,
перетворимо в рівності (4) подвійний
інтеграл на поверхневий:
;
.
Для поверхні, заданої рівнянням
,
напрямні косинуси нормалі обчислюються
за формулами:
;
;
,
де
,
,
звідки ми отримуємо
(6). Використавши (5), (6), з рівності (4)
отримаємо
(7). Аналогічно можна отримати формули:
(8),
(9), де
,
– неперервно диференційовні функції
на поверхні
,
заданій рівнянням
.
За формулами (7), (8), (9)можемо записати:
Цю
формулу (10) називають формулою Стокса.
Позначивши вектор
,
врахувавши означення циркуляції і
потоку векторного поля, суть формули
(10) можемо сформулювати в наступній
теоремі. Теорема (Стокса). Циркуляція
векторного поля
по контуру
дорівнює потоку (вихора) вектора
через поверхню
,
натягнуту на контур
,
тобто
(11) (формула Стокса у векторній формі).
Також, врахувавши рівності
,
,
,
формулу (10) можна записати у вигляді:
.
Зауважимо, що з формули (12) отримаємо
формулу Гріна, якщо
за поверхню
взяти плоску область
на площині
.
Справді, поклавши
,
з формули (12) отримуємо
.