15. Формула Гріна.

Формула Гріна встановлює зв'язок між подвійним інтегралом і криволінійним інтегралом 2 роду.

Розглянемо подвійний інтеграл Запишемо його вигляді повторного інтеграла, а саме, = (*). Кожен із отриманих інтегралів може бути замінений криволінійним інтегралом:

= Ці інтеграли дорівнюють нулю, оскільки відрізки PS, RQ є перпендикулярними до осі Ox. Тоді = + + + =

Аналогічно отримаємо формулу (*)

Віднімаючи почленно від рівності (*) рівність(**) отримаємо

17. Поверхневий інтеграл I роду; Обчислити його.

Нехай проста поверхня, задана рівнянням = і на цій поверхні визначена неперервна функція F(x,y,z). Подвійний інтеграл наз. поверхневим інтегралом I роду від функції F(x,y,z) по поверхні і позначають . Отже за означенням . Використавши формулу dS= = отримаємо вираз для обчислення інтеграла І роду:

. Якщо поверхня задана явним рівнянням z=f(x,y), то формула набуде вигляду .

Приклад. Обчислити поверхневий інтеграл де -поверхня конуса z=x +y , 0≤z≤1,

18.Криволінійний інтеграл 2 роду; обчислення.

Якщо вздовж кривої (АВ) визначені функції P(x,y) і Q(x,y) і існують інтеграли і , то суму цих двох інтегралів називають загальним криволінійним інтегралом 2 роду і позначають так: . Аналогічно виводять поняття криволінійного інтеграла 2 роду по просторовій кривій (АВ). Нехай на кривій (АВ) задана функція f(x,y,z). Будуємо аналогічно міркуючи отримаємо.

Обчислення :

У випадку просторової кривої яка задана параметричними рівняннями x= , y= z= де , де , - неперервно диференційовані функції на відрізку[ ], криволінійний інтеграла обчислюється за фоммулою dt

Випадок коли плоска крива АВ задана явним рівнянням y= , де = неперервнодиференційовна функція на проміжку [a,b]. Тоді взявши за параметр x=t формула криврл. Інтегралу набуде вигляду , якщо рівняння кривої задано x= , с то

19.Теорема про рівність нулеві криволінійного інтеграла 2 роду по простому замкненому контуру.

Теорема: Нехай в однозв’язній області G , функції P(x,y), Q(x,y) визначені і неперервні зі своїми похідними . Для того щоб виконувалася рівність (*) де L-простий заикнутий контур в області G виконувалася рівність (**).

Необхідність. Нехай виконується рівність (*) тоді за формулою Гріна (***)де D G.

Припустимо що рівність (*) виконується а умова (**) не виконкється хоч би в одній точці тобто в точці М (x ,y ) D. Нехай >0 в точці М . оскільки є неперервною функцією в області G,то це означає що вираз буде додатнім в деякому достатньому малому околі точки М . Тобі , що суперечить умові (***) . наше припущення не правильне. Отже

Достатність. Дано . Довести що Візьмемо довільний контур L, що обмежує область D G. За формулою Гріна

20.Звязок криволінійного інтегралу 2 роду з повним диференціалом функції(відновлення функції F(x,y)).

Для того щоб вираз Pdx + Qdy був повним диференціалом деякої функції F(x,y), необхідно і досить виконання рівності .

Дано: вираз Pdx+Qdy є поданим диференціалом функції F(x,y). Доведемо що оскільки повний диференціал функції F(x,y), то і оскільки - неперервні функції, то за теоремою пропро рівність мішаних похідних = , а це означає що .

21. Зведення потрійного інтегралу до повторного.

Обчислення потрійного інтеграла зводиться до обчислення повторного інтеграла як і у випадку з подвійними інтегралами.Нехій функція f(x,y,z) є неперервною в деякій замкненій області V . А це означає, що існує потрійний інтеграл від функції f(x,y,z) по області V. Розглянемо область у вигляді паралелепіпеда

П={(x,y,z):a }, який проектується на площину Ozy в прямокутник R={(y,z): }. Аналогічно,як і для подвійного інтеграла,доводять наступну теорему: Якщо для функції f(x,y,z)існує протрійний інтеграл і при кожному x існує подвійний інтеграл = , то існує повторний інтеграл і виконується рівність = .

Перейшовши в подвійному інтегралі до повторного отримаємо =

22. Зміна змінних у подвійному інтегралі;Перехід до полярних координат.

//Розглянемо подвійний інтеграл де D- область, обмежена простим кусково-гладким контуром L,a функція є неперервною в обл. D x=x( ), y=y( ). Для того щоб змінити зміння перш за все потрібно розбит область D’ на n частинок ( ), де D’ область на площині O . потім розбивається область D на

Переглянемо перехід в подвійному інтегралі до полярних координат: x= де праві частини є неперервно диференційованими функціями за змінними і . Якобіан

І( ) = = =

Звідци ми отримуємо , де -улумент площі в полярних координатах,D-область інтегрування в декартовій системі координат, D -область інтеграла в полярній системі

23. Обчислення площ та об’ємів за допомогою подвійного інтегралу.

Обчислити площу плоскої фігури D обмеженими лініями: x=a, x=b, y=Y(x), y=Y (x).

На рис. D має вигляд: S=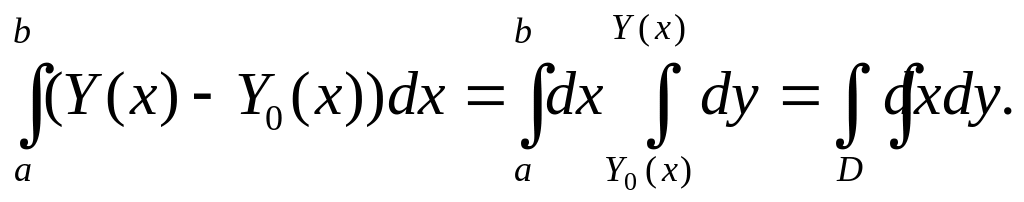

Нехай тіло (V) обмежене поверхнями z=f (x,y), z=f (x,y), де функції f (x,y), f (x,y) визначені в області спільній D. Рис.

f (x,y)

Лего показати що об’єм V обчислюється за формулою: V=

24.Зведення подвійного інтегралу до повторного на елементарній області(л8п6)

Теорема.6. нехай - елементарна відносно осі Oy область, функція f(x,y) інтегрована в області і для кожного існує інтеграл

Тоді має місце формула

￮ Нехай c=

Очевидно, що область лежить в прямокутнику .

Побудуємо функцію F(x,y) таким чином:

(2)

Оскільки функція F(x,y) інтегрована на множині і на , то існує подвійний інтеграл Існують для кожного інтеграли

Отже виконуються всі умови теореми про зведення подвійного інтегралу до повторного. Тому

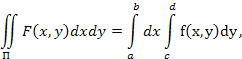
Підставивши(2) в останню формулу отримаємо рівність (1).

Наслідок. Для функції f(x,y) неперервної в області виконується формула (1)

25. Подвійний інтеграл та його властивості.(л8п3,4)

Розглянемо тіло V, яке зверху обмежене поверхнею , визначена на деякій області G ); з боку тіло обмежене циліндричною поверхнею; в основі маємо плоску область G:

Щоб обчислити об’єм тіла V використаємо традиційний в інтегральному численні спосіб. А саме:

1. Робиваємо шукану величину на елементарні частини

2. Наближено обчислюємо ці елементарні частини і сумуємо їх

3. Переходимо до границі суми

В даному випадку розбиває сіткою кривих область G на частинки . Позначимо площі цих частинок . Розглянемо циліндричні стовпчики , які мають основи і в сукупності складають тіло V.

Для обчислення об’єму циліндричного стовпчика візьмемо в кожній частині точку і побудуємо циліндр з основою , площа якої і висота .Об’єм такого елементарного циліндра дорівнює добутку і приблизно дорівнює об’ємові , тобто .

Тоді об’єм тіла V наближано обчислюється за формулою

(1)

Права частина рівності 1 є інтегральною сумою для функції , обмеженої в області G . Позначивша через - найбільший з діаметрів областей і перейшовши при до границі(якщо вона існує) отримаємо подвійний інтеграл

, який позначають .

Властивості подвійного інт. є аналогічними до властивостей кратного:

1.Правильна рівність

Справді для довільного розбиття Т виконується рівність

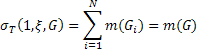
2. Якщо і – інтегрована на вимірна за Жорданом множині G функція, то

3.Якщо - інтегровані на множині G функції, а і - довільні дійсні числа, то і функція є інтегрованою на G причому

4. якщо і - інтегровані на множині G функції і при , то

5.Якщо функція f(x) неперервна на зв’язному вимірному компакті G, то знайдеться точка така, що

6. Якщо є розбиття множини G , то функція є інтегрованою на множині G тоді і тільки тоді, коли вона інтегрована на кожній із множин , причому

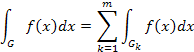
7.Добуток інтегрованих на вимірній множині G функцій є інтегрована на множині G функція.

8. Якщо функція інтегрована на вимірній множині G , то функція також інтегрована і

26. Циліндричні координати

Положення точки M(x,y,z) в координатні системі Oxyz однозначно визначається трьома числами ρ,φ,z – криволінійними координатами, де ρ – довжина радіус-вектора проекції точки М на площину Оху, φ – кут, що утворює цей радіус-вектор з віссю Ох, ξ – апліката точки М. Числа ρ,φ,z (або ρ,φ, ξ) називаються циліндричними координатами точки М. Циліндричні координати пов'язані з декартовими координатами співвідношеннями:

x = ρcosφ, y = ρsinφ, z = ξ, (1) при чому ρ≥0, 0≤φ<2 π , -∞< ξ <+∞. Відображення, яке задано рівностями (1) є неперервно диференційованим і якобіан цього відображення:

I =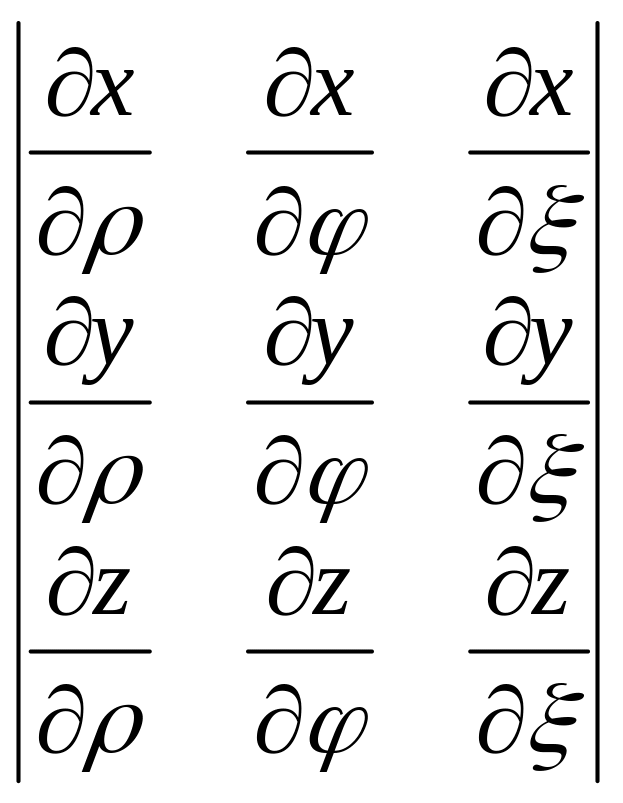 = = 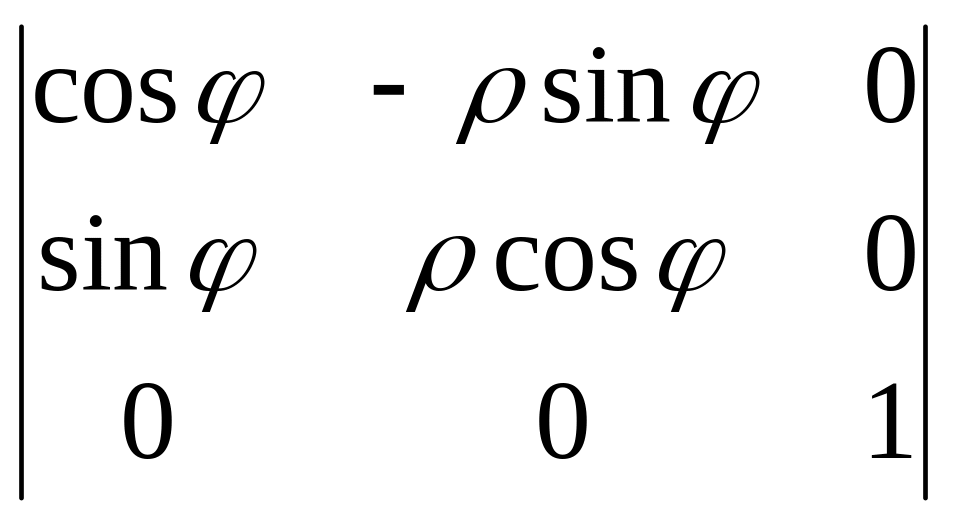ρ.

Запишем формулу:

= , де ρdρdφdz – елемент об'єму в циліндричних координатах.