18.Способы решения систем тригонометрических уравнений.

Спосабы:

-с помощью единичной окружности

-с помощью координатной прямой

-аналитически

Спосабы решения:

-подстановка

-алгебраическое сложение

Основные приёмы:

-возведение обеих частей уравнения в квадрат или куб

-почленное деление обеих частей уравнения или двух уравнений на одно и то же выражение, отличное от нуля

-замена неизвестных

-Разложение на множетели

Особенности решения систем тригонометрических уравнений;

-решения простейших уравнений

-для записи каждого из уравнений системы употребляются различные параметры (n,k,l и др.)

-одно из уравнений системы сводится к уравнению относительно одной переменной.

Рассмотрим некоторые типы систем тригонометрических уравнений и укажем наиболее употребительные методы решения систем, основываясь на общей теории систем уравнений.

Замечание. Обратим внимание на типичную ошибку, которую допускают учащиеся и абитуриенты при записи решений систем тригонометрических уравнений. Дело в том, что параметры   и   появляются при решении разных уравнений системы и независимы друг от друга. Поэтому эти параметры должны обозначаться разными буквами. Обозначение их одним символом ведет к потере решений.

В некоторых случаях системы тригонометрических уравнений можно свести к алгебраическим системам.

Аналогично можно находить решения систем вида

  

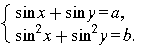
и

  

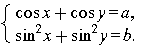
Решая системы тригонометрических уравнений с двумя неизвестными, следует выяснить, нельзя ли выразить одно неизвестное через другое и свести задачу к решению уравнения с одним неизвестным.

19.Методы доказательства тригонометрических неравенств.

20.Алгоритм решения неравенства sinx˂ a,ǀ aǀ≤ 1.

Неравенство  . Если   , то решением неравенства является любое число, так как синус всегда меньше или равен 1. Если   , то это неравенство решения не имеет, так как синус не может быть меньше -1. Рассмотрим теперь случай, когда а лежит на полуинтервале   .   Ответ:   .

21. Алгоритм решения неравенства cosx˂ a,ǀ aǀ≤ 1.

Неравенство   . Если   , то решением неравенства является любое число, так как косинус всегда меньше или равен 1. Если   , то это неравенство решения не имеет, так как косинус не может быть меньше -1. Рассмотрим теперь случай, когда а лежит на полуинтервале   .   Ответ:   .

22. Алгоритм решения неравенства tgx˃ a.

Неравенство  :   

23. Алгоритм решения неравенства ctgx˂ a.

Неравенство   :