- •1.Основные тригонометрические тождества.
- •2.Формулы приведения и правила их применения.
- •3.Формулы сложения, двойного и тройного угла.
- •4.Формулы половинного угла.
- •5.Формулы преобразования суммы(разности) в произведение.
- •6.Формулы преобразования произведения в сумму(разность).
- •12.Основные приемы преобразования тригонометрических выражений.
- •13.Способы доказательства тригонометрических тождеств.
- •14.Решение простейших уравнений.
- •16.Решение однородных уравнений и сводящихся к ним.
- •18.Способы решения систем тригонометрических уравнений.
- •19.Методы доказательства тригонометрических неравенств.
- •23. Алгоритм решения неравенства ctgx˂ a.
1.Основные тригонометрические тождества.
sin² α + cos² α = 1
tg α · ctg α = 1
tg α = sin α ÷ cos α
ctg α = cos α ÷ sin α
1 + tg² α = 1 ÷ cos² α
1 + ctg² α = 1 ÷ sin² α
2.Формулы приведения и правила их применения.
Все формулы приведения получаются из соответствующих формул сложения.
Применение формул приведения можно свести к использованию мнемонического правила:
Определяется название приведенной функции по следующему правилу: если аргумент приводимой функции имеет вид
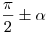 или
или  ,
то функция меняется на сходственную,
если аргумент приводимой функции имеет
вид
,
то функция меняется на сходственную,
если аргумент приводимой функции имеет
вид 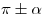 ,
то функция названия не меняет.
,
то функция названия не меняет.Определяется координатная четверть, в которой лежит аргумент приводимой функции, в предположении, что
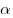 —
острый угол, и определяется знак
приводимой функции в этой четверти.
—
острый угол, и определяется знак
приводимой функции в этой четверти.
Формулы приведения
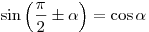 ;
;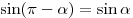 ;
;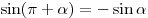 ;
;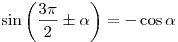 ;
;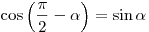 ;
;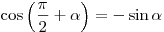 ;
;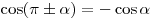 ;
;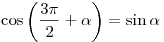 ;
;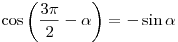 ;
;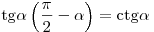 ;
;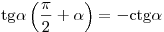 ;
;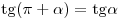 ;
;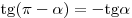 ;
;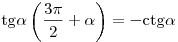 ;
;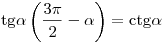 .
.
3.Формулы сложения, двойного и тройного угла.
|
|
Формулы сложения аргументов |
|
|
(4) |
|
(5) |
|
(6) |
|
|
Формулы двойного угла выводятся из формул (4), (5) , (6) и (7), если принять, что угол β равен углу α:
Формулы двойного угла |
|
|
(23) |
|
(24) |
|
(25) |
|
|
Формулы тройного угла |
|
|
|
|
4.Формулы половинного угла.

Если
в первой и во второй формуле
заменить 2![]() на t,
получим
формулы, которые называются понижение
степени и удвоения
угла:
cos2t=21+cos2t; sin2t=21−cos2t/
на t,
получим
формулы, которые называются понижение
степени и удвоения
угла:
cos2t=21+cos2t; sin2t=21−cos2t/
5.Формулы преобразования суммы(разности) в произведение.
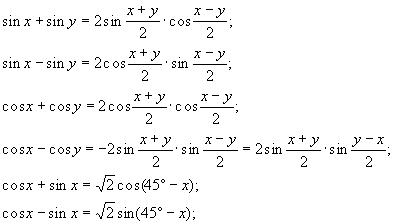
6.Формулы преобразования произведения в сумму(разность).
![]() ,
,
![]() ,
,
![]() .
.
7.Функции y=sinx, y=arcsinx и их свойства.
y=sinx
а) Область определения: D (sin x) = R .
б) Множество значений: E (sin x) = [ – 1 , 1 ] . в) Четность, нечетность: функция нечетная.
г)
Периодичность:
функция периодическая с основным
периодом T = 2![]() .
.
д) Нули
функции:
sin x =
0 при x =
n, n ![]() Z.
Z.
е) Промежутки знакопостоянства:
![]() ;
; ![]() .
.
ж) Промежутки
монотонности:
![]() ;
;
![]() .
.
з) Экстремумы:
![]() ;
; ![]() .
.
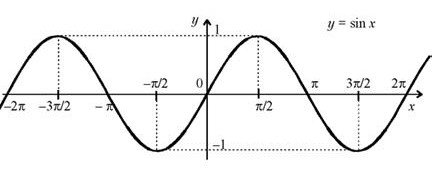
График функции y= sin x изображен на рисунке.
Арксинусом
числа y
[
– 1, 1] называется такая
дуга ![]() ,
синус которой равен y,
т.е.
,
синус которой равен y,
т.е.
![]() L
L ![]() .
.
Функция x = arcsin y является обратной к функции y = sin x на отрезке . Для исходной и обратной функций привычнее аргументы и функцию обозначать одними и теми же буквами: y = sin x, y = arcsin x.
В
таких обозначениях графики
указанных функций симметричны
относительно прямой y
= x.
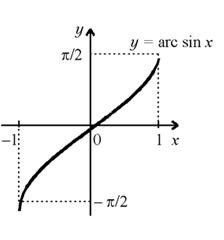
Поэтому, нарисовав график
функции y =
sin x на
отрезке ![]() и
симметрично отобразив
его относительно прямой
y
= x,
получим график арксинуса.
и
симметрично отобразив
его относительно прямой
y
= x,
получим график арксинуса.
8.Функция y=cosx, y=arccosx и их свойства.
y=cosx
а) Область определения: D (cos x) = R .
б) Множество значений: E (cos x ) = [ – 1 , 1 ] . в) Четность, нечетность: функция четная.
г) Периодичность: функция периодическая с основным периодом T = 2 .
д) Нули
функции:
cos x =
0 при x = ![]() +
n, n
Z.
+
n, n
Z.
е) Промежутки знакопостоянства:
![]() ;
;
![]() .
.
. ж) Промежутки монотонности:
![]() ;
;
![]() .
.
з) Экстремумы:
![]() ;
; ![]() .
.
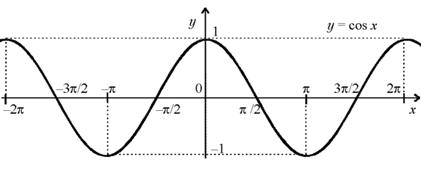
График функции y= cos x изображен на рисунке.
Арккосинусом числа y [– 1, 1] называется такая дуга x [ 0 , ], косинус которой равен y, т.е.
![]() L
L ![]() .
.
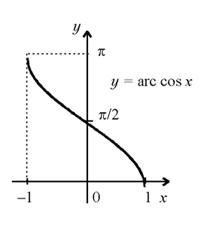
Функция x = arccos y является обратной к функции y = cos x на отрезке x [ 0, ]. Для исходной и обратной функций привычнее аргументы и функцию обозначать одними и теми же буквами: y = cos x, y = arccos x. График функции y = arccos x приведен на рисунке.
9. Функция y=tgx, y=arctgx и их свойства.
y=tgx
а) Область определения: D (tg x) = R \ { /2 + n( n Z ) }.
б) Множество значений: E (tg x ) = R . в) Четность, нечетность: функция нечетная.
г) Периодичность: функция периодическая с основным периодом T = .
д) Нули функции: tg x = 0 при x = n, n Z.
е) Промежутки знакопостоянства:
![]() ;
;
![]() .
.
ж) Промежутки монотонности: функция возрастает на каждом интервале, целиком принадлежащем ее области определения.
з) Экстремумы: нет.
График функции y = tg x изображен на рисунке.
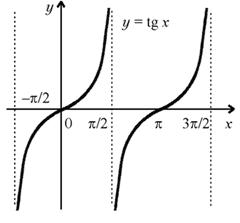
Арктангенсом
числа y
R
называется такая дуга ![]() ,
тангенс которой равен y,
т.е.
,
тангенс которой равен y,
т.е.
![]() L
L ![]() .
.
Функция x = arctg y явлется обратной к функции, y = tg x на интервале . Для исходной и обратной функций привычнее аргументы и функцию обозначать одними и теми же буквами: y = tg x, y = arctg x. График функции y = arctg x приведен на рисунке.
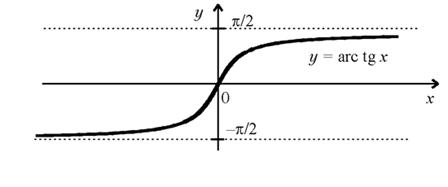
10. Функция y=ctgx, y=arcctgx и их свойства.
y=ctgx
а) Область определения: D (ctg x) = R \ { n( n Z ) }.
б) Множество значений: E (ctg x ) = R . в) Четность, нечетность: функция нечетная.
г) Периодичность: функция периодическая с основным периодом T = .
д) Нули функции: ctg x = 0 при x = /2 + n, n Z.
е) Промежутки
знакопостоянства ;
![]() ;
; ![]() .
.
ж) Промежутки монотонности: функция убывает на каждом интервале, целиком принадлежащем ее области определения.
з) Экстремумы: нет.
График функции y = ctg x изображен на рисунке.
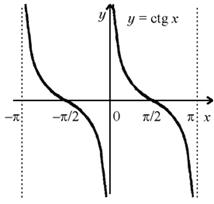
Арккотангенсом числа y R называется такая дуга x [ 0 , ], котангенс которой равен y, т.е.
![]() L
L ![]() .
.
Функция x = arcctg y является обратной функции y =ctg x на интервале x (0, ). Для исходной и обратной функций привычнее аргументы и функцию обозначать одними и теми же буквами: y = ctg x, y = arcctg x . График функции y = arcctg x приведен на рисунке.
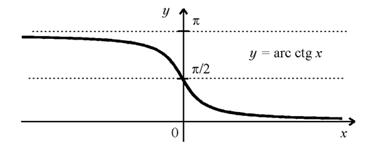
11. Функция y=secx, y=cosecx и их свойства.
sec (–α) = sec α |
cosec (–α) = – cosec α |
|
|||||||||||||
sec (α + 2kπ) = sec α |
cosec (α + 2kπ) = cosec α
|
|
|||||||||||||
|
|
|
|
|
|
|
|||||||||
Функция |
|
Область определения |
|
Множество значений |
|
Четность |
|
Участки монотонности (k = 0, ± 1, ± 2,…) |
|||||||
cosec x |
|
pk |
|
|
|
нечетная |
|
возрастает при x О ((4k + 1) p/2, (4k + 3) p/2), убывает приx О ((4k – 1) p /2, (4k + 1) p/2) |
|||||||