7. Список использованной литературы.
[0]
А. С. Монин,
А. М. Яглом, Статистическая
гидромеханика,
М.: Наука. Физматгиз, ч.1,2,
[1]
Ландау
Л. Д., Лифшиц Е. М. Теоретическая
физика. –
Издание 5-е. –
2006. –
Т. VI. Гидродинамика.
[2]
Сабельфельд
К.К.,
Решение
краевых задач методом Монте-Карло. –
Новосибирск: Наука, 1980, 154 с.
[3]
Kraichnan
R.H.,
Diffusion by a Random Velocity Field. – The Physics of Fluids,
1970, vol. 13, N 1, p. 22-31.
[4]
R. Sandberg, H. Fasel, Direct Numerical Simulations of Transitional
Supersonic Base Flows, AIAA Journal, Vol. 44, No. 4, April 2006.
[5]
Боровская
И.А.,
Моделирование случайных сигналов и
полей в задачах аэроакустики. – Москва,
Институт математического моделирования
РАН, 2007, автореферат на соискание ученой
степени кандидата физико-математических
наук, 3-5 с.
[6]
Вадзинский
Р.Н. Справочник
по вероятностным распределениям. - СПб.:
Наука, 2001, 295 с.
[7]
N.
Metropolis, S. Ulam, The
Monte Carlo Method, — J. Amer. statistical assoc.
1949 44 № 247
335—341.
[8]
А.
М. Обухов, Турбулентность
и динамика атмосферы,
Гидрометеоиздат, 412,[1] с. ил. 23 см Л.
Гидрометеоиздат 1988.
7. Приложение.
Рис.1.
Поля X
и Y
составляющих скоростей, построенные
на различных высотах Z.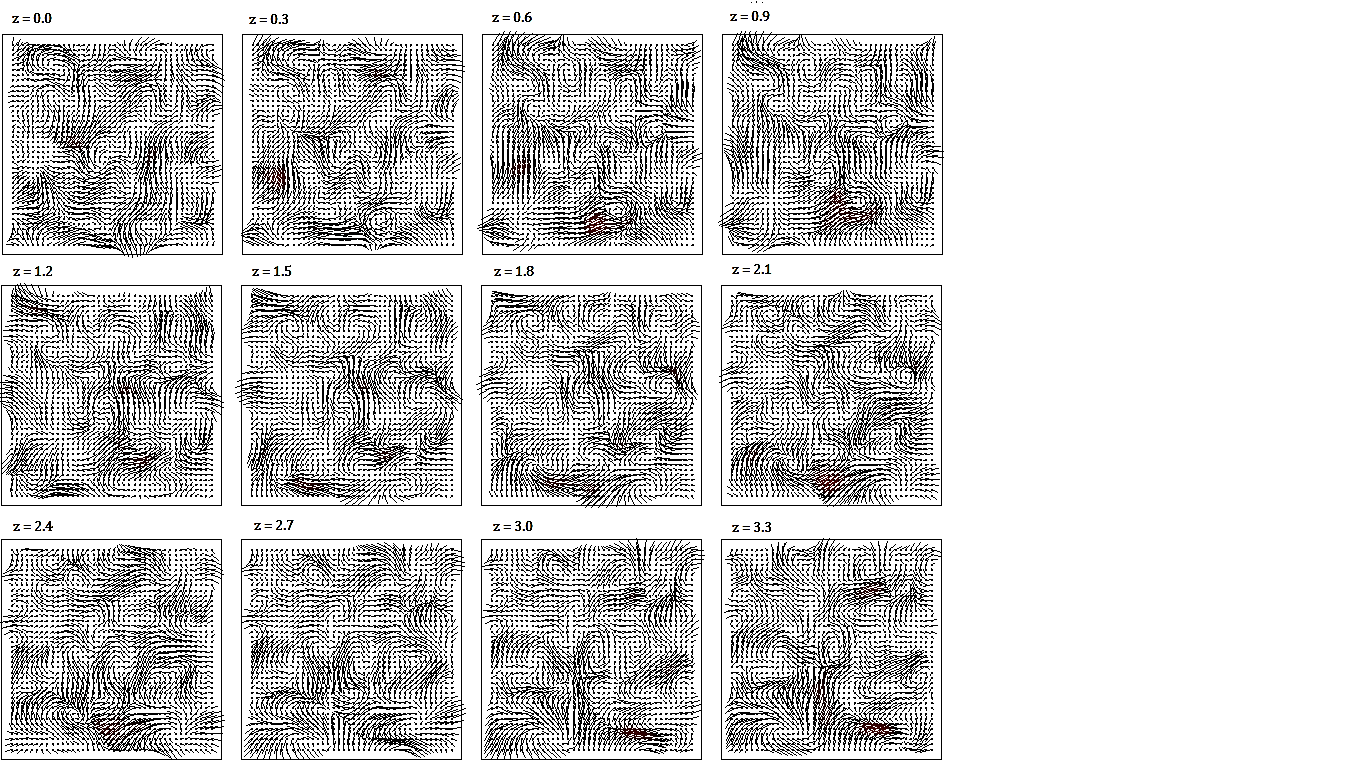
Рис.2.
График теоретической поперечной и
продольной составляющих корреляционной
функции.
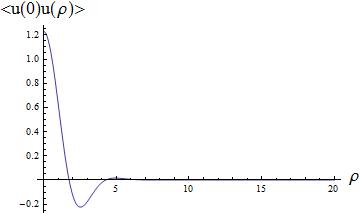
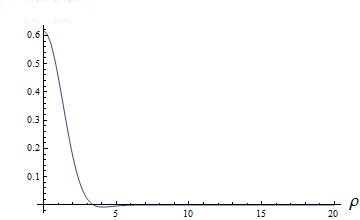
Рис.
2а. Продольная и две поперечных корреляция
при числе гармоник = 10.
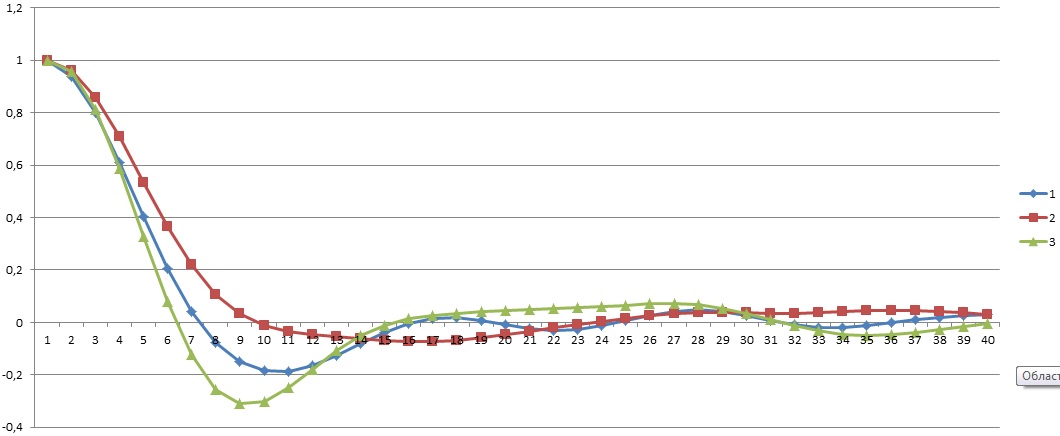
Рис.
2б. Корреляция при N
= 100.
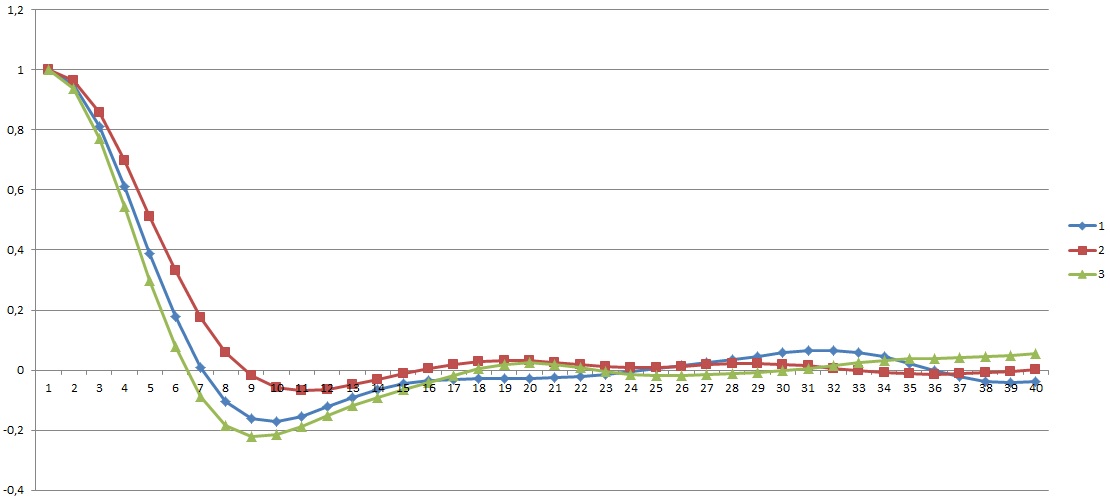
Рис.
2в. Корреляция при N
= 1000 .
.
Рис.
3. Сравнение теоретического и посчитанного
спектра при N
= 100.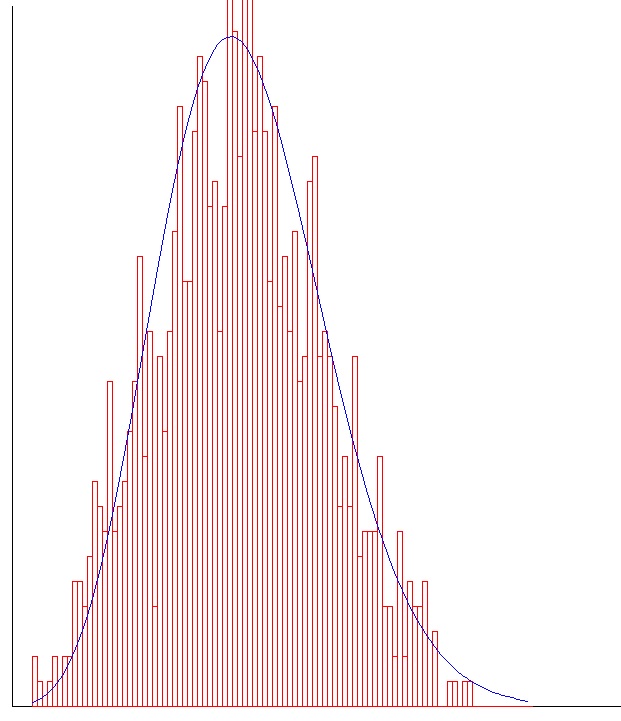
8. Контакты:
Стерлинг
Григорий Григорьевич
Sterling239@mail.ru
8
(929) 503-52-08
19







 .
.