26 Вопрос.
В основе алгоритма сложения многозначных чисел лежат следующие теоретические факты:
способ записи чисел в десятичной системе счисления;
свойства коммутативности и ассоциативности сложения;
дистрибутивность умножения относительно сложения;
В общем виде алгоритм сложения натуральных чисел, записанных в десятичной системе счисления, формулируют так:
1. Записывают второе слагаемое под первым так, чтобы соответствующие разряды находилось друг под другом.
2. Складывают единицы первого разряда. Если сумма меньше десяти, записывают ее в разряд единиц ответа и переходят к следующему Разряду (десятков).
3. Если сумма единиц больше или равна десяти, то представляют ее в виде а0 + b0 = 1 × 10 + с0, где с0 - однозначное число; записывают с0 в разряд единиц ответа и прибавляют 1 к десяткам первого слагаемого, после чего переходят к разряду десятков.
4. Повторяют те же действия с десятками, потом с сотнями и т.д. Процесс заканчивается, когда оказываются сложенными цифры старших разрядов. При этом, если их сумма больше или равна десяти, то приписываем впереди обоих слагаемых нули, увеличиваем нуль перед первым слагаемым на 1 и выполняем сложение 1 + 0 = 1.Заметим, что в этом алгоритме (как и в некоторых других) для краткости употребляется термин «цифра» вместо «однозначное число, изображаемое цифрой».
Ошибки при выполнении письменного сложения, обусловленные забыванием единиц того или иного разряда, которые надо было запомнить, а при вычитании - единиц, которые занимали.
Сложением натуральных чисел называется алгебраическая операция, определенная на множестве N натуральных чисел и обладающая свойствами:
I) (" а Î N) а + 1 = а¢
II) (" а, b Î N) а + b¢ = (а + b)¢
Суммой натуральных чисел а и b называется число элементов в объединении непересекающихся множеств А и В
а + b = n(А) + n(В) = n(А È В)
1) Коммутативный закон сложения
(" а, b Î N) а + b = b + а
2) Ассоциативный закон сложения
(" а, b, с Î N) (а + b) + с = а + (b + с)
3) Монотонность сложения
(" а, b, с Î N) а < b Þ а + с < b + с
4) Монотонность сложения
(" а, b, с, d Î N) а < b Ù с < d Þ
а + с < b + d
5) (" а Î N) а + 0 = а
27Вопрос.
Разностью натуральных чисел а и b называется натуральное число с = а – b, удовлетворяющее условию b + с = а
с = а – b Û b + с = а
Действие, с помощью которого находится разность, называется вычитанием.
Это действие обратное сложению
Вычитание натуральных чисел связано с выделением подмножества из множества
Пусть А и В конечные множества,
n(А) = а, n(В) = b, В Í А
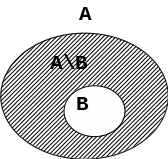
Разностью натуральных чисел а и b называется число элементов в разности множеств А и В
а - b = n(А) - n(В) = n(А \ В)
Разностью натуральных чисел а и b называется число элементов в дополнении подмножества В до множества А
а - b = n(А) - n(В) = n(В‘А)
Разность натуральных чисел можно рассматривать как меру отрезка с, дополняющего отрезок b до отрезка а, мерами которых являются числа q и р
Теорема о существовании и единственности разности
Разность целых неотрицательных чисел а и b существует тогда и только тогда, когда b £ а. Если разность чисел а и b существует, то она единственна.
Свойства вычитания