3.3. Теплопроводность через однослойную цилиндрическую стенку

Рассмотрим однородную цилиндрическую стенку (трубу) длиной l, м, с внутренним радиусом r₁ и внешним r₂. Коэффициент теплопроводности материала постоянен и равен λ. Внутренняя и внешняя поверхности поддерживаются при постоянных температурах t₁ и t₂, причем t₁>t₂ (рис.3.4), и температура изменяется только в радиальном направлении r.

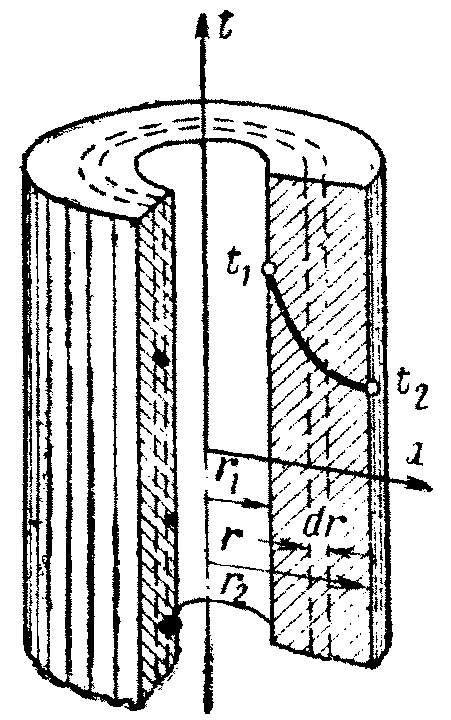
Рис. 3.4. Однородная цилиндрическая стенка

Следовательно, температурное поле здесь будет одномерным, а изотермические поверхности цилиндрическими, имеющими с трубой общую ось. Выделим внутри стенки кольцевой слой радиусом r и толщиной dr, ограниченный изотермическими поверхностями. Согласно закону Фурье количество тепла, проходящего в единицу времени через этот слой, равно:

(3.13)

Разделив переменные, имеем:

(3.14)

После интегрирования уравнения (3.14) находим:

(3.15)

Подставляя значения переменных на границах стенки (при r = r₁

t= t₁ и при r = r₂ t= t₂) и исключая постоянную С, получаем следующую расчетную формулу:

(3.16)

Следовательно, количество тепла, переданное в час через стенку трубы, прямо пропорционально коэффициенту теплопроводности λ, длине l и температурному напору Δt = t₁ - t₂ и обратно пропорционально натуральному логарифму отношения внешнего диаметра трубы d₂ к внутреннему d₁. Формула (3-16) справедлива и для случая, когда t₁<t₂, т.е. ког­да тепловой поток направлен от наружной поверхности к внутренней.

Количество тепла, проходящее через стенку трубы, может быть отнесено либо к единице длины l, либо к единице внутренней F₁ или внешней F₂ поверхности трубы. При этом расчетные формулы соответственно принимают следующий вид:

(3.17)

(3.18)

(3.19)

Так как внутренняя и внешняя поверхности трубы по величине различны, то различными получаются и значения удельных тепловых потоков q₁ и q₂. Взаимная связь между ними определяется соотношением

q_l =πd₁q₁=πd₂q₂ или d₁ q₁=d₂q₂

Величина q_l, Вт/м², называется линейной плотностью теплового потока.

Уравнение температурной кривой внутри однородной цилиндрической стенки выводится из уравнения (3.15) Подставляя сюда значения Q и С, имеем:

(3.20)

Следовательно, в этом случае при постоянном значении λ температура изменяется по логарифмической кривой (см. рис.3.4).

Рис. 3.5. Многослойная цилиндрическая стенка

3.4. Теплопроводность через многослойную цилиндрическую стенку

Пусть цилиндрическая стенка состоит из трех разнородных слоев. Диаметры и коэффициенты теплопроводности отдельных слоев известны, их обозначения см. на рис.3.5. Кроме того, известны температуры внутренней и внешней поверхностей многослойной стенки t₁ и t₄.

В местах же соприкосновения слоев температуры неизвестны, обозначим их через t₂ и t₃. При стационарном тепловом режиме через все слои проходит одно и то же количество тепла. Поэтому на основании (3.17) можно написать:

(3.21)

Из этих уравнений определяется температурный перепад в каждом слое

(3.22)

Сумма этих перепадов составляет полный температурный напор. Складывая отдельно левые и правые части системы (3.22) имеем:

(3.23)

из которого определяется значение теплового потока q_l

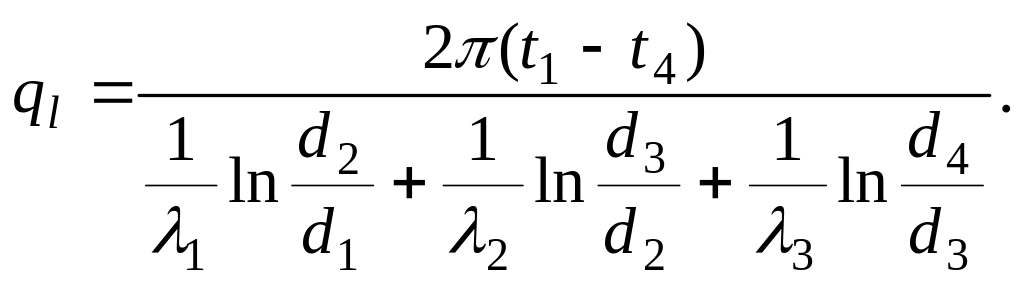(3.24)

По аналогии с этим сразу можно написать расчетную формулу для n-слойной стенки

(3.25)

Значения неизвестных температур t₂ и t₃ поверхностей соприкосновения слоев определяются из (3.22):

(3.26)

Согласно (3.20) внутри каждого слоя температура изменяется по логарифмическому закону, для многослойной стенки в целом температурная кривая представляет собой ломаную кривую (см. рис. 3.5).