10.4. Метод регулярного режима

Рассмотрим процесс охлаждения (или нагревания) твердого тела, когда условия охлаждения – температура окружающей среды t_ж и коэффициент теплоотдачи α – во времени остаются постоянными и внутренние источники тепла в теле отсутствуют. В отношении начального распределения температур в теле не будем делать никаких ограничений, за исключением того, что примем условие: разность между температурой в любой точке тела и температурой окружающей среды в начальный момент имеет один и тот же знак. При этих условиях нестационарный процесс охлаждения (нагревания) тела может быть разделен на две стадии: начальную стадию и стадию регулярного режима.

Первая стадия характеризуется тем, что изменение температурного поля во времени существенно зависит от особенностей начального теплового состояния тела, и поэтому характер процесса не определяется однозначно условиями охлаждения и свойствами тела. Однако постепенно влияние начальных условий все более и более утрачивается; напротив, воздействие условий охлаждения и физических свойств тела становится опреде­ляющим. Наступает регулярный тепловой режим. При этом закон изменения температурного поля во времени принимает простой и универсальный вид: логарифм избыточной температуры тела в любой его точке изменяется во времени по линейному закону:

(10.8)

т.е. эта температура убывает во времени по экспоненциальному закону

(10.9)

Величина m, 1/с, есть положительное число, не зависящее от координат и времени. Эта величина характеризует интенсивность охлаждения (нагревания) тела и называется темпом охлаждения (нагревания).

Рис. 10.5. Изменение температуры во времени при охлаждении тела

Графическая интерпретация рассматриваемого процесса показана на рис. 10.5; здесь приведены кривые изменения величин ln и ln для двух фиксированных точек тела 1 и 2 во времени на про­тяжении всего процесса охлаждения тела. Наступление регулярного режима характеризуется тем, что соответствующие кривые переходят в прямые линии, имеющие одинаковый угловой коэффициент на графике, т. е. они оказываются параллельными между собой.

Применим уравнение (10.8) к двум произвольным моментам времени τ′ и τ″ (рис. 10.5) и, исключив постоянную С, получим:

(10.10)

Формула (10.10) дает способ определения величины темпа охлаждения m из опыта; для этого необходимо измеренные в какой-нибудь точке тела, температуры представить в полулогарифмической системе координат на прямолинейном участке полученной зависимости выбрать две точки и соответствующие им величины и τ подставить в формулу (10.10).

Основные закономерности регулярного теплового режима были подробно исследованы Г.М. Кондратьевым, который раскрыл основные связи, существующие между темпом охлаждения m, с одной стороны, и физическими свойствами тела, его формой, размерами и условиями охлаждения, – с другой. Это позволило разработать способы приближенного расчета нестационарных температурных полей, методы моделирования нестационарных процессов в сложных объектах, дать оценки неравномерности температурных полей в различных условиях и т. д. На основе теории ре­гулярного режима были предложены и получили широкое распространение на практике новые методы определения теплофизических свойств веществ: α, λ, с, термических сопротивлений R, степени черноты тел ε, коэффициентов теплоотдачи α . Преимуществом таких методов является простота техники эксперимента, высокая точность получаемых результатов и малая затрата времени на проведение опытов.

Для регулярного теплового режима характерны следующие основные положения:

1. Основное соотношение (10.8), определяющее наступление регулярного режима, выполняется не только для однородных простых тел, но также для любых сложных систем из разнородных тел. т.е. явление регуляризации температурного поля имеет общий характер.

2. Темп охлаждения однородного тела m при конечном значении коэффициента теплоотдачи пропорционален коэффициенту теплоотдачи α и внешней поверхности тела F и обратно пропорционален полной теплоемкости тела Cv=сρV:

(10.11)

3. При α→∞ значение m_∞ для любой сложной системы конечно, причем величина m_∞ для однородных тел пропорциональна коэффициенту температуропроводности а материала:

(10.12)

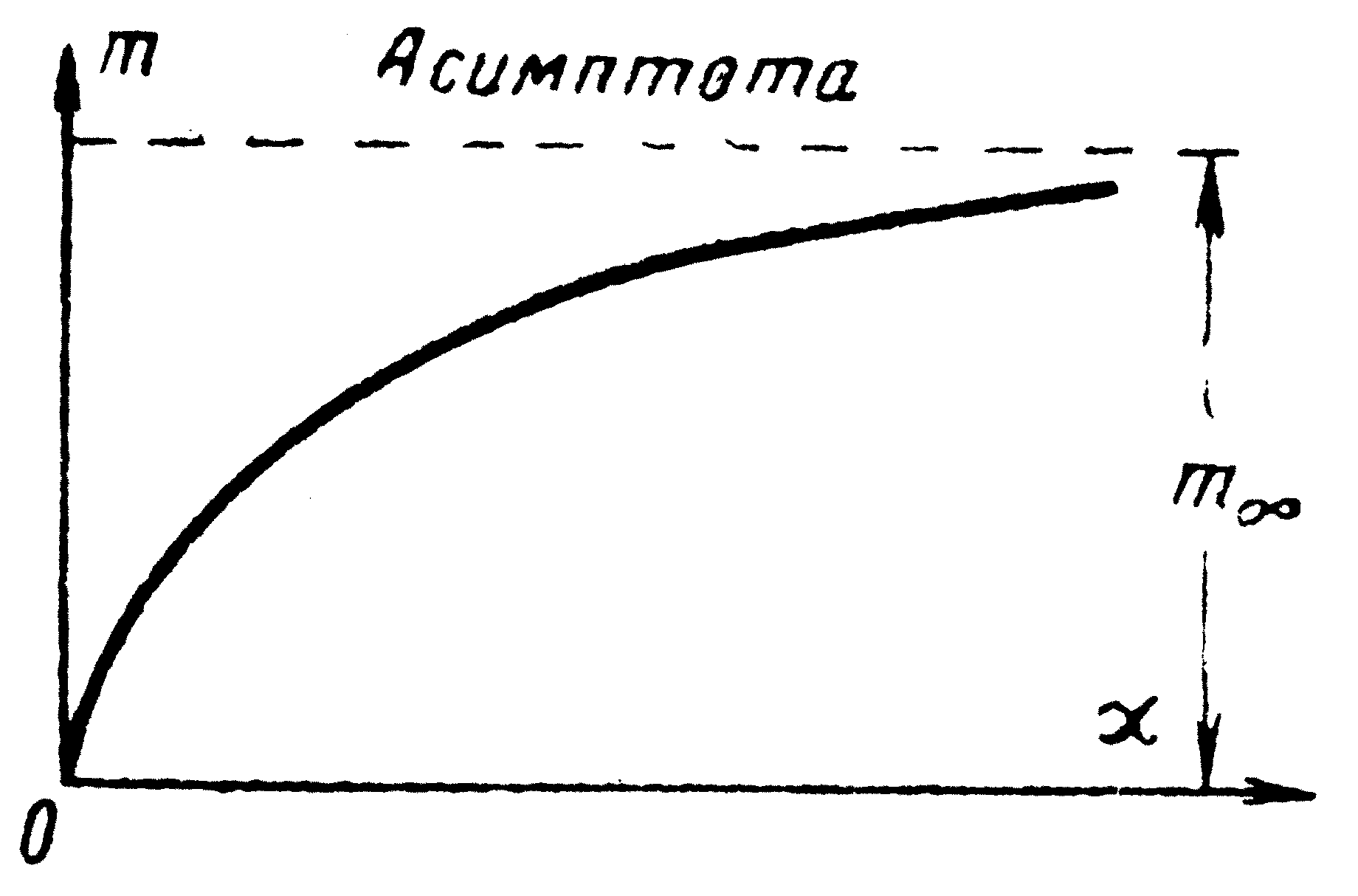
Соотношение (10.11) есть выражение закона сохранения энергии для условий регулярного режима охлаждения (нагревания) тел. Величина Ψ в этом уравнении представляет собой отношение средней по поверхности избыточной температуры к сред­ней по объему величине , . Это отношение в течение всего периода регулярного режима остается постоянным и называется параметром неравномерности температурного поля; величина Ψ может изменяться от 0 до 1 (последний случай отвечает равномерному полю температур в теле).

Коэффициент К в соотношении (10.12) имеет размерность м² и зависит лишь от геометрических свойств – формы и размера тела. Его называют коэффициентом формы. Для тел простой формы величины К были определены аналитически.

ТЕСТЫ

1. Температурное поле при нестационарном режиме характеризуется уравнением:

а) б) в) г) д)

2. Толщина горячей пластины неограниченной длины составляет 2δ = 400 мм; коэффициент теплопроводности

коэффициент теплоотдачи при охлаждении пластины в наружном воздухе Коэффициент температуропроводимости Критерий Био (Bi) равен:

а) 2,0; б) 0,2; в) 1,0; г) 1,8; д) 0,8.

3. Критерий Фурье (Fo) этой же пластины после охлаждения в течении 1 ч (3600 с) равен:

а) 0,8; б) 0,5; в) 1,2; г) 0,3; д) 1,5.

4. Горячая цилиндрическая болванка диаметром d = 60 мм и длиной l=700 мм охлаждается в воздухе, температура которого постоянна. Болванка выполнена из стали, плотность и теплоёмкость которой равна: ρ=7900 кг/м³; с = 460 Дж/(кг ^. К). Режим регулярный; темп охлаждения m=16,7 ^. 10^–5 1/с. Коэффициент неравномерности распределения темпе-ратуры принять = 1. Коэффициент теплоотдачи , при охлаждении тела равен:

а) 20,2; б) 8,8; в) 10,5; г) 5,1; д) 9,7.