2) Проделаем то же самое для рациональной функции . Имеем
или
,
т.е.
.
Из последнего соотношения, (приравнивая
коэффициенты при
,)
получаем:
Следовательно,
и
.
Замечание. Иногда для нахождения коэффициентов A, B, … удобно подставлять конкретные значения х, особенно корни знаменателя. Например, рассмотрим разложение:
или
.
Пусть
,
тогда
и
.
Возьмем
,
тогда
и
.
Подводя промежуточный итог заметим, что раз любую рациональную функцию можно представить в виде суммы многочлена и простейших рациональных функций, то для вычисления интеграла от любой рациональной функции достаточно научиться интегрировать простейшие рациональные функции.
Интегрирование простейших рациональных функций
В соответствии с таблицей неопределенных интегралов получаем, что
и
(интеграл
от степенной функции).
Следовательно, осталось только научиться интегрировать простейшие второго рода.
Рассмотрим
сначала пример. Вычислим неопределенный
интеграл
.
1
шаг.
Выделим в знаменателе полный квадрат,
тогда
;
2
шаг.
Сделаем замену переменных
,
тогда
,
и
;
3
шаг.
Поделим почленно числитель на знаменатель
и воспользуемся свойством линейности
интеграла. Получаем, что
;
4
шаг.
В первом интеграле сделаем замену
переменных
,
тогда
,
и
.
Таким
образом, проделав последовательно
перечисленные выше шаги, сможем вычислить
неопределенный интеграл от любой
простейшей вида
.
В частности легко показать, что
,
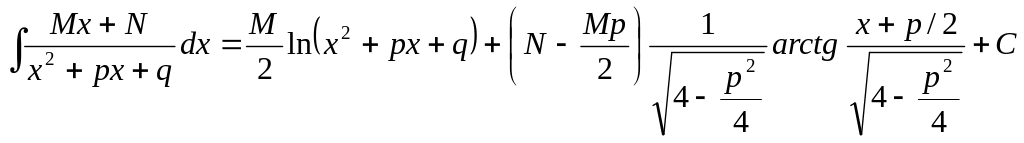где
.
Таким образом, получаем следующую схему интегрирования рациональных функций:
1. Если подынтегральная функция является неправильной рациональной функцией, то представляем её в виде многочлена и правильной рациональной функции.
2. Раскладываем знаменатель правильной рациональной функции на множители первой и второй степени согласно теореме 3.
3. Представляем правильную рациональную функцию в виде суммы простейших.
4. Интегрируем по перечисленным выше правилам.
Рассмотрим пример использования данной схемы.
Пример
9.
Вычислим интеграл
.
Решение.
1) Подынтегральная функция является неправильной рациональной функцией. Поделим числитель на знаменатель с остатком
Следовательно,
.
2)
Разложим знаменатель на множители
.
Дискриминант последнего сомножителя
меньше нуля.
3) Представим рациональную функцию в виде суммы простейших
.
Тогда
и
Следовательно,
.
Таким
образом,
.
4) Вычислим последний интеграл отдельно, выполняя последовательно перечисленные выше шаги.
.
Окончательно получаем, что
.
Варианты для самостоятельной работы.
Вычислить данные интегралы. В первых 2 примерах проверить результата дифференцированием.
1.
,
,
,
,
,
.
2.
,
,
,
,
,
.
3.
,
,
,
,
,
.
4.
,
,
,
,
,
.
5.
,
,
,
,
,
.
6.
,
,
,
,
,
.
7.
,
,
,
,
,
.
8.
,
,
,
,
,
9.
,
,
,
,
,
.
10.
,
,
,
,
,
.
11.
,
,
,
,
,
.
12.
,
,
,
,
,
.
13.
,
,
,
,
,
.
14.
,
,
,
,
,
.
15.
,
,
,
,
,
.
16.
,
,
,
,
,
.
17.
,
,
,
,
,
18.
,
,
,
,
,
.
19.
,
,
,
,
,
.
20.
,
,
,
,
,
.
21.
,
,
,
,
,
.
22.
,
,
,
,
,
.
23.
,
,
,
,
,
.
24.
,
,
,
,
,
.
25.
,
,
,
,
,
.
26.
,
,
,
,
,
27.
,
,
,
,
,
.
28.
,
,
,
,
,
.
29.
,
,
,
,
,
.
30.
,
,
,
,
,
.
31.
,
,
,
,
,
.
32.
,
,
,
,
,
.
33.
,
,
,
,
,
.
34.
,
,
,
,
,
.
35.
,
,
,
,
,
36.
,
,
,
,
,
.
37.
,
,
,
,
,
.
38.
,
,
,
,
,
.
39.
,
,
,
,
,
.
40.
,
,
,
,
,
.
41.
,
,
,
,
,
.
42.
,
,
,
,
,
.
43.
,
,
,
,
,
.
44.
,
,
,
,
,
45.
,
,
,
,
,
.