Неопределенный интеграл

Определение 1. Функция называется первообразной для функции на множестве , если для всех из .

Пример 1.

1) первообразная для , так как . Аналогично, также первообразная для , потому что .

2) первообразная для , так как .

Свойства первообразных.

1. Если - первообразная для , то также первообразная для .

2. Если и - две первообразные для функции , то существует константа такая, что

.

Свойства 1 и 2 можно объединить в одно следующим образом.

3. Множество всех первообразных функции имеет вид: , где , а - произвольное число.

Определение 2. Неопределенным интегралом от функции называется множество всех первообразных функции .

Неопределенный интеграл обозначается , где - знак интеграла, - подынтегральная функция, - подынтегральное выражение.

Таким образом,

, (1)

где - некоторая первообразная для , - произвольная постоянная.

Пример 2. По определению 2 и примеру 1 имеем: .

Операция нахождения неопределенного интеграла от функции называется интегрированием этой функции.

Свойства неопределенного интеграла

1. Производная от неопределенного интеграла равна подынтегральной функции, т.е.

.

2. Дифференциал неопределенного интеграла равен подынтегральному выражению, т.е.

.

3. Неопределенный интеграл от производной некоторой функции равен этой функции с точностью до постоянного слагаемого, т.е.

.

4. Постоянный множитель можно выносить за знак интеграла, т.е.

,

где - некоторое число.

5. Интеграл от алгебраической суммы двух функций равен такой же сумме интегралов, т.е.

.

Таблица неопределенных интегралов

1. .	2. .
3. , частный случай .
4. .	5. .
6. .	7.
8. , частный случай
9. , частный случай .
10. .	11. .

Пример 3. Вычислим несколько интегралов, используя таблицу и свойства.

1) (формула № 1).

2) (Формула № 1).

3) .

4)

(5 свойство и формула № 1).

5)

(5 свойство и формулы № 6 и 8).

Метод замены переменной в неопределенном интеграле

Теорема 1. Если и - функция, дифференцируема на рассматриваемом промежутке, то

(2)

Следствие. Если - первообразная для функции , то

,

где и - числа, .

Формула (2) позволяет упростить искомый интеграл, а в отдельных случаях свести его к табличному.

Рассмотрим несколько примеров вычисления интегралов по теореме 1.

Пример 4.

1) Пусть . Положим . Тогда и . В итоге получаем, что

.

2) Найдем интеграл . Пусть , тогда и (формула № 2) .

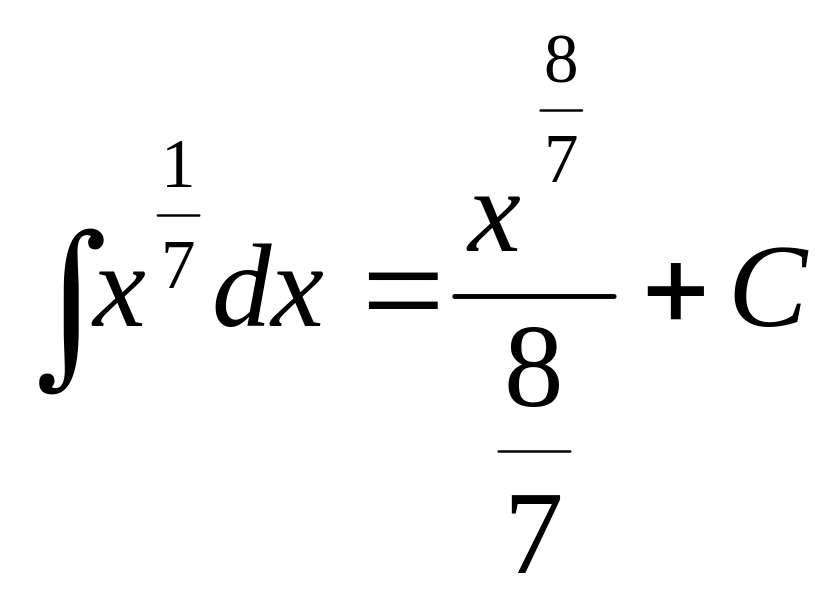3) Найдем интеграл . В этом случае воспользуемся следствием из теоремы 1, так как , а , то 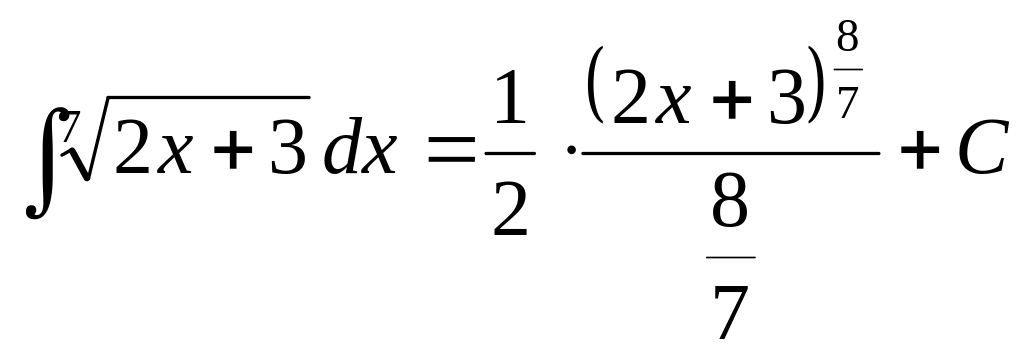по следствию из теоремы 1 ( ).

Замечание. В примерах 4.1 и 4.2 также можно было воспользоваться следствием из теоремы 1.

4) Приведем еще несколько примеров использования следствия. Несложно убедиться, что

;

;

.

Проверим два последних результата дифференцированием. По теореме о производной сложной функции имеем:

;

.

В обоих случаях после дифференцирования получили подынтегральную функцию.

5) Вычислим интеграл . Пусть , тогда и .

Иногда удобнее сразу искать , а не , как это будет показано в следующих примерах.

6) Найти интеграл . Положим , тогда , полученное равенство позволяет выразить , последнее является сомножителем подынтегрального выражения. В итоге получаем, что .

7) Рассмотрим интеграл . Если , то и .

8) Вычислим интеграл . Пусть , тогда и .

Замечания.

1) Новую переменную можно не выписывать явно. Например, интеграл можно записать как , или интеграл .

При таком подходе говорят о введении (внесении) функции под знак дифференциала.

2) Часто при вычислении одного и того же интеграла можно применять несколько замен. Например, при вычислении интеграла можно сделать замену или .

3) Существуют функции, первообразные которых нельзя выразить через элементарные функции. Интегралы от таких функций называются “неберущимися” в элементарных функциях. Например, , и т.д.