2. О возможности замены пероксида лауроила в инициирующей композиции на 1,1,5-тригидроперфторпентилпероксидикарбонат

Обычно при полимеризации винилхлорида суспензионным способом используется смесь как минимум двух инициаторов. Более активный инициатор (имеющий большую константу скорости распада) применяется для «запуска» процесса полимеризации, в то время как инициатор с меньшей константой скорости распада позволяет довести реакцию до высоких конверсий уже после того, как основная часть более активного инициатора разложилась [1]. Одним из примеров такой комбинации инициаторов, использующейся для полимеризации винилхлорида, является смесь н-бутоксиэтилпероксидикарбоната (KCS) и пероксида лауроила. Последний имеет константу скорости распада в 30 раз меньшую, чем у KCS (при 60°С). Известно, что полифторированные пероксидикарбонаты имеют меньшую константу устойчивости по сравнению с нефторированными, а применение их в качестве инициаторов полимеризации винилхлорида позволяет получать полимер, обладающей повышенной термостабильностью и светостойкостью [21]. Улучшение характеристик полимера связано с введением в макромолекулы в качестве концевых групп полифторалкильных фрагментов, а также с причинами, рассмотренными в предыдущем разделе. С учётом сказанного представляет научный интерес изучение возможности замены пероксида лауроила в инициирующей композиции на фторированный пероксидикарбонат. Для проведения такого исследования на основании литературных данных была предложена математическая модель, описывающая зависимость конверсии винилхлорида от времени и тепловыделения от времени при различных концентрациях инициаторов в полимеризационной смеси.

1. Уравнения и параметры кинетической модели суспензионной полимеризации винилхлорида

В процессе суспензионной полимеризации винилхлорид диспергируется в воде до мелких капель диаметром от микрометра до миллиметра. Каждая такая капля ведёт себя как система, в которой протекает блочная полимеризация. Через очень непродолжительное время после начала реакции в каждой такой капле сосуществуют две фазы: обогащённая мономером фаза (и практически полностью из него состоящая ввиду практически полной нерастворимости полимера в винилхлориде) и фаза, в основном содержащая полимер. Можно предположить, что первая фаза состоит исключительно из мономера, а во второй фазе содержится мономер в количестве, определяемом его растворимостью в полимере. По мере протекания процесса масса фазы 1 уменьшается, в то время как масса фазы 2 увеличивается. Когда конверсия достигает заданного значения X_f, фаза 1 исчезает и начинается поглощение мономера, находящегося в газовой фазе, а, значит, и падение давления в реакторе. Таким образом, кинетическая модель включает в себя два этапа полимеризации, описываемых различными уравнениями. Для описания участка с конверсиями X<X_f использована основанная на работе [24]. Ниже приведён список допущений и уравнений, используемых в применённой модели:

При X<X_f:

1. Процесс полимеризации проводится при постоянной температуре T

2. Рассматривается одновременное действие трёх инициаторов

3. Эффективность инициирования f для каждого из инициаторов принята равной единице

4. Концентрация и константа диссоциации каждого инициатора принята одинаковой в обеих рассматриваемых фазах.

Последнее условие выражается следующими уравнениями:

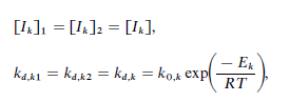
Где k = 1,2,3, индекс 1 обозначает фазу мономера, индекс 2 – полимерную фазу.

Концентрация k-го инициатора в зависимости от времени выражается соотношением:

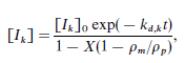
Знаменатель этого выражения отражает изменение объёма системы по мере протекания реакции, ρ_m/ρ_p – отношение плотностей мономера и полимера.

Общая концентрация свободных радикалов в каждой фазе при выполнении условия квазистационарности определяется следующими уравнениями:

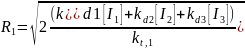
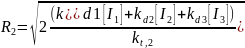
где k_t,1 и k_t,2 – константы скорости обрыва в фазах 1 и 2 соответственно. Их зависимость от температуры задаётся следующими соотношениями:

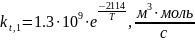
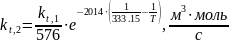
Выражение для k_t,2 взято из работы [25].

Концентрация мономера в каждой из фаз:

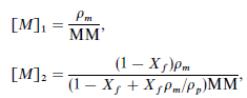где MM – молярная масса мономера.

Основное кинетическое уравнение для конверсии:

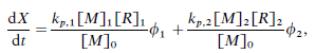
где k_p,1 и k_p,2 – константы скорости роста цепи, [M]₀ – начальная концентрация мономера, равная концентрации мономера в первой фазе (т.к. она не меняется со временем – объём фазы 1 пропорционален количеству вещества мономера в ней), φ₁ и φ₂ – объёмная доля фаз 1 и 2 соответственно.

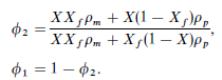
Константы скорости роста цепи полагаются равными для фаз 1 и 2 и определяются соотношением из работы [25]

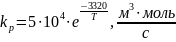
Критическое значение конверсии X_f задаётся соотношением

Плотности мономера и полимера в зависимости от температуры определяются соотношениями

, где θ – температура в °C

Полученное дифференциальное уравнение вида 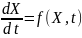решалось численным методом Рунге – Кутта четвёртого порядка.

Для высоких конверсий X>X_f применена более простая модель, описанная и параметризованная в работах [26,27] и модифицированная на случай использования нескольких инициаторов.

Суть её в следующем. Поскольку в области значений X>X_f эффективность инициирования, константа скорости обрыва цепей и константа скорости роста цепи падают с ростом конверсии, в работе [26] предложено учесть этот эффект, полагая, что комбинация этих величин пропорциональна (1-X). Уравнения модели следующие:

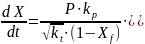
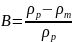
Параметризация для P дана в работе [27]:

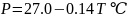
Для согласования двух моделей в точке X=X_f, пользуясь условием равенства производной 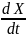, определяемой из двух моделей, в выражение для при X>X_f введён дополнительный множитель, численно равный 1,55 при всех температурах.

Скорость изменения конверсии связана со скоростью выделения теплоты в любой момент времени следующим соотношением:

, где m_D – общая масса загружаемого винилхлорида, -ΔH=25,33 ккал/моль.