1.Неопределённый интеграл.  Если функция          является первообразной для         , то выражение          называется неопределённым интегралом от функции          и обозначается символом      Решить неопределенный интеграл   – это значит ПРЕВРАТИТЬ его в определенную функцию  , пользуясь некоторыми правилами, приемами и таблицей. Функция          называется первообразной от функции          на отрезке         , если во всех точках этого отрезка выполняется равенство         . 

Свойства неопределённого интеграла

Свойство 1. Производная от неопределённого интеграла равна подынтегральной функции, то есть если         , то 

 Свойство 2. Дифференциал от неопределённого интеграла равен подынтегральному выражению 

Свойство 3. Неопределённый интеграл от дифференциала некоторой функции равен сумме этой функции и произвольной константы 

Свойство 4. Неопределённый интеграл от суммы функций равен сумме неопределённых интегралов 

 Свойство 5. Неопределённый интеграл от разности функций равен соответствующей разности неопределённых интегралов 

Свойство 6. Постоянный множитель можно выносить за знак интеграла 

Свойство 7. Если  то

Вопрос2 Метод подведения под знак дифференциала основан на равенстве .

То есть, главной задачей является приведение подынтегральной функции к виду  . Поэтому желательно иметь перед глазами таблицу производных основных элементарных функций. Перепишем ее в виде дифференциалов

Пример:  

  , . где .

Идея метода замены состоит в том, чтобы сложное выражение (или некоторую функцию) заменить одной буквой.

Метод интегрирования по частям решает очень важную задачу, он позволяет интегрировать некоторые функции, отсутствующие в таблице, произведение функций, а в ряде случаев – и частное.

1)  ,  ,   

2)  ,  – экспоненциальная функция, умноженная на какой-нибудь многочлен.

3)  ,  ,   – тригонометрические функции, умноженные на какой-нибудь многочлен.

4)  ,   – обратные тригонометрические функции («арки»), «арки», умноженные на какой-нибудь многочлен.

ВОПРОС3. Интегрирование выражений, содержащих квадратный трехчлен Для вычисления неопределенных интегралов вида ,  необходимо выполнить следующие действия: 1) выделить из квадратного трехчлена ax² + bx + c полный квадрат: ; 2) выполнить в интеграле подстановку  . 3) получившийся интеграл представить в виде суммы двух интегралов, один из которых является табличным, а другой – вычисляется способом внесения переменной t под знак дифференциала:  .

Пример 1. 

. Пример 2. .

Вопрос 4. Пример 1. Найти интеграл

         Подынтегральная функция является правильной рациональной дробью. Разложение на неприводимые сомножители знаменателя имеет вид   Это означает, что разложение подынтегральной функции в сумму простейших дробей имеет следующий вид:

 

Найдем коэффициенты разложения комбинированным методом:

                 

Таким образом,

Вопрос 7. Основной приём решения иррациональных интегралов – это замена переменной, которая избавит нас от ВСЕХ корней в подынтегральной функции. , Потому что  , и в результате замены корень пропадёт. Проведем замену: 

Проведем замену:

Вопрос 8. Криволинейной трапецией называется плоская фигура, ограниченная графиком некоторой функции , осью и прямыми , :

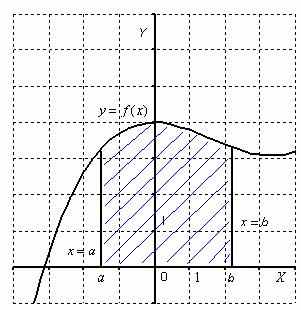
Площадь криволинейной трапеции численно равна определенному интегралу 

 С точки зрения геометрии определенный интеграл – это ПЛОЩАДЬ.  То есть,  определенному интегралу (если он существует) геометрически соответствует площадь некоторой фигуры.

Есть ли у определенного интеграла геометрический смысл? Есть. И очень хороший. Самая популярная задача – вычисление площади с помощью определенного интеграла.

Что значит решить определенный интеграл? Решить определенный интеграл – это значит, найти число.

Как решить определенный интеграл? С помощью знакомой со школы формулы Ньютона-Лейбница:

ВОПРОС 9  определенному интегралу (если он существует) геометрически соответствует площадь некоторой фигуры. Например, рассмотрим определенный интеграл  . Подынтегральная функция   задает на плоскости некоторую кривую (её можно всегда при желании начертить), а сам определенный интеграл   численно равен площади соответствующей криволинейной трапеции.

Вычислить площадь фигуры, ограниченной линиями  ,  ,  ,  ..В данной задаче решение может выглядеть так. Выполним чертеж (обратите внимание, что уравнение   задает ось  ):

Штриховать криволинейную трапецию я не буду, здесь очевидно, о какой площади идет речь. Решение продолжается так:

На отрезке    график функции   расположен над осью  , поэтому:

Ответ: 

Вопрос 10. Вычислить несобственный интеграл – это значит, найти ЧИСЛО (точно так же, как в определенном интеграле), или доказать, что он расходится (то есть, получить в итоге бесконечность вместо числа).

1). Несобственный интеграл с бесконечным пределом (ами) интегрирования

Иногда такой несобственный интеграл еще называют несобственным интегралом первого рода. В общем виде несобственный интеграл с бесконечным пределом чаще всего выглядит так:  . Несобственный интеграл   численно равен площади заштрихованной фигуры, при этом возможны два случая: 1) Первое, мысль, которая приходит в голову: «раз фигура бесконечная, то  », иными словами, площадь тоже бесконечна. Так быть может. В этом случае говорят, что, что несобственный интеграл расходится.

2) Но. Как это ни парадоксально прозвучит, площадь бесконечной фигуры может равняться… конечному числу! Например:  . Может ли так быть? Запросто. Во втором случае несобственный интеграл сходится.

2). Несобственные интегралы от неограниченных функций

Иногда такие несобственные интегралы называют несобственными интегралами второго рода. Несобственные интегралы второго рода коварно «шифруются» под обычный определенный интеграл и выглядят точно так же:  . Но, в отличие от определенного интеграла, подынтегральная функция   терпит бесконечный разрыв (не существует): 1) в точке  ,  2) или в точке  , 3) или в обеих точках сразу, 4) или даже на отрезке интегрирования. 

ВОПРОС11. Дифференциальное уравнение первого порядка, содержит:  1) независимую переменную  ; 2) зависимую переменную   (функцию); 3) первую производную функции:  . Дифференциальным уравнением называется такое уравнение, которое содержит производные от искомой функции и может содержать искомую функцию и независимую переменную.   Порядком дифференциального уравнения называется наивысший порядок, входящих в него производных. Решением дифференциального уравнения называется всякая функция y = φ (x), которая при подстановке в уравнение обращает его в верное равенство. Общим решением дифференциального уравнения называется такое его решение, содержащее произвольные постоянные, из которого любое частное решение может быть получено при соответствующем подборе произвольных постоянных. Частное решение дифференциального уравнения — это решение, не содержащее произвольных постоянных. Аналогично определяются общий интеграл и частный интеграл дифференциального уравнения.

Задача Коши

Каждое конкретное решение, т. е. каждая конкретная функция, которая удовлетворяет данному дифференциальному уравнению и не зависит от произвольных постоянных, называется частным решением, или частным интегралом . Чтобы получить частные решения (интегралы) из общих, надо постоянным   придают конкретные числовые значения.

График частного решения называется интегральной кривой . Общее решение, которое содержит все частные решения, представляет собой семейство интегральных кривых. Для уравнения первого порядка это семейство зависит от одной произвольной постоянной, для уравнения n -го порядка - от n произвольных постоянных.

Задача Коши заключается в нахождении частного решение для уравнения n -го порядка, удовлетворяющее n начальным условиям:

по которым определяются n постоянных с 1 , с 2 ,..., c n.