23.Предельный признак сравнения. Признак Даламбера.

Предельный: Пусть существует . В этом случае: 1) С≠0, P и Q сходятся или расходятся одновременно. 2) с=0, из сходимости Q следует сходимость P, а их расходимости P следует расходимость Q.

Даламбер: Если для ряда с положительными членами u₁+u₂+u₃+…+u_n+u_n+1+…=

u_n˃0 выполняется условие , то ряд сходится при l<1 и расходится при l˃1. Признак Даламбера не дает ответа, если l=1. В этом случае для исследования ряда применяются др.приемы.

24.Знакопеременный ряд. Абсолютная и условная сходимость.

Для знакопеременного ряда существует понятие абсолютной условной сходимости. Знакопеременный ряд S= называется абсол. Сходящимся, если сходится ряд из абсолютных величин его членов, т.е. сходится знакоположительный числовой ряд . Знакопеременный ряд условно сходящийся, если ряд расходится, а ряд сходится.

25.Степенные ряды. Теорема Абеля.

Функциональный ряд , где C_n- числовая послед-ть наз-ся степенным рядом.

ПР:

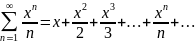
Степенной ряд сходится на интервале (x₀-R, x₀+R) с центром в точке х₀.

Число R- радиус сходимости степенного ряда может быть вычислено по формулам: R= или R=

Степенной ряд сходится равномерно на любом отрезке, целиком лежащим внутри сходимости. Сходимость степенного ряда на границах интервала сходимости необходимо исследовать специально для конкретного ряда.

Теорема Абеля

• Если степенной ряд сходится при некоторых х= , где -число неравное нулю, то он сходится абсолютно при всех значениях таких что <

• если ряд сходится при х= , то он расходится при всех значениях х, таких что ˃

26. Разложение функций в степенные ряды. Ряд Тейлора.

При исследовании св-в бесконечно дифференцируемых функций изучают их степенные ряды – ряды Тейлора.

• Пусть функция f(x) определена в некоторой окрестности точки х₀ и имеет в этой точке производные всех порядков.

Ряд Т(х)= наз-ся рядом Тейлора f(x) в точке х₀

ф-ия f(x) может быть разложена в степенной ряд на интервале (x₀-R, x₀+R) если существует степенной ряд, сходящийся к f(x) на этом интервале, т.е. f(x)=

• Пусть функция f(x) бесконечто диффериенцируема на интервале (x₀-R, x₀+R) и все её производные ограничены в совокупности на этом интервале, т.е. существует число M>0, такое, что для всех Х€(x₀-R, x₀+R) и для всех n=1,2.. справедливо нер-во | (x)|≤M. Тогда ряд Тейлора сходится к f(x) для всех Х€(x₀-R, x₀+R).

27. Функции спроса и предложения.

Спрос – это количество товаров (услуг), которое покупатели готовы приобрести на рынке.

Величина спроса зависит от ряда факторов. Такую зависимость принято называть функцией спроса.

Qda = f (Pa, Pb...z, K, L, M, N, T), (10.1)

где Qda– функция спроса на товар; Pa– цена товара; Pb...z– цены других товаров, в том числе товаров-заменителей и сопутствующих; K – денежные доходы покупателей; L – вкусы и предпочтения людей; M – потребительские ожидания; N – общее число покупателей; T – накопленное имущество людей.

Основной фактор спроса – цена товара, поэтому зависимость можно упростить:

Qda= f(Pa).(10.2)

Функцию спроса можно представить также в виде графика (рис. 10.1).

Функция спроса

Соединение между собой точек на графике, каждая из которых является конкретной комбинацией цены и количества, позволяет построить кривую спроса D.

Предложение – это количество товаров (услуг), которое продавцы готовы продать на рынке. Как и спрос, оно зависит от ряда факторов и может быть формализовано.

Qsa = f (Pa, Pb...z, C, K, R, N), (10.3)

где Qsa– предложение товара; Pa– цена товара; Pb...z – цены других товаров, в том числе товаров-заменителей и сопутствующих; C – наличие проиводственных ресурсов; K – применяемая технология (время); R – налоги и дотации у производителей; N – число продавцов.

Основной фактор предложения – тот же, что и спроса – цена.

Qsa = f (Pa). (10.4)

Функцию предложения также можно задать с помощью таблицы, которую легко перевести в график (рис. 10.2).

Функция предложения

Соединение точек на графике позволяет построить кривую предложения S, которая имеет восходящий вид.