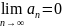- •Квадратный корень, функция
- •2.Предел функции.
- •3.Основные теоремы о пределах.
- •4.Непрерывность функции в точке и на интервале.
- •5.Производная и дифференциал.
- •6. Основные теоремы о дифференцируемых функциях
- •7.Функции нескольких переменных и их непрерывность.
- •8. Производные функции нескольких переменных
- •9. Дифференциалы функции нескольких переменных.
- •10. Поиск экстремума функции одной переменной.
- •11. Поиск экстремума функции двух переменных.
- •12. Неопределенный интеграл, основные теоремы.
- •Свойства неопределённого интеграла:
- •13.Интегрирование подстановкой.
- •15. Интегрирование рациональных функций.
- •16. Определенный интеграл, основные теоремы.
- •17. Понятие о дифференциальном уравнении: его порядке, общем и частном решении.
- •18. Дифференциальные уравнения первого порядка: с разделяющимися переменными.
- •19. Линейные дифференциальные уравнения, однородные и неоднородные. Понятие общего решения линейного уравнения.
- •20. Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами.
- •21. Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами. Метод Лагранжа вариации произвольных постоянных.
- •22. Числовой ряд. Сходимость и сумма ряда. Свойства сходящихся числовых рядов. Необходимое условие сходимости ряда.
- •23.Предельный признак сравнения. Признак Даламбера.
- •24.Знакопеременный ряд. Абсолютная и условная сходимость.
- •25.Степенные ряды. Теорема Абеля.
- •26. Разложение функций в степенные ряды. Ряд Тейлора.
- •27. Функции спроса и предложения.
- •28.Функция полезности. Кривые безразличия.
20. Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами.
Рассмотрим
линейное дифференциальное уравнение
вида
![]()
где
p, q
− постоянные коэффициенты.
Для
каждого такого дифференциального
уравнения можно записать так называемое
характеристическое
уравнение:
![]()
Обшее решение однородного дифференциального уравнения зависит от корней характеристического уравнения, которое в данном случае будет являться квадратным уравнением. Возможны следующие случаи:
Дискриминант характеристического квадратного уравнения положителен: D > 0. Тогда корни характеристического уравнения k1 и k2 действительны и различны. В этом случае общее решение описывается функцией
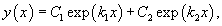 где
C1
и C2
− произвольные действительные числа.
где
C1
и C2
− произвольные действительные числа.
Дискриминант характеристического квадратного уравнения равен нулю: D = 0. Тогда корни действительны и равны. В этом случае говорят, что существует один корень k1 второго порядка. Общее решение однородного дифференциального уравнения имеет вид:
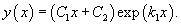
Дискриминант характеристического квадратного уравнения отрицателен: D < 0. Такое уравнение имеет комплексно-сопряженные корни k1 = α + βi, k1 = α − βi. Общее решение записывается в виде
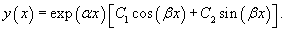
21. Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами. Метод Лагранжа вариации произвольных постоянных.
Структура общего решения
Линейное
неоднородное уравнение данного типа
имеет вид:
![]()
где p, q − постоянные числа (которые могут быть как действительными, так и комплексными). Для каждого такого уравнения можно записать соответствующее однородное уравнение:
![]()
Теорема: Общее решение неоднородного уравнения является суммой общего решения y0(x) соответствуюшего однородного уравнения и частного решения y1(x) неоднородного уравнения:
![]()
Метод вариации постоянных
Если общее решение y0 ассоциированного однородного уравнения известно, то общее решение неоднородного уравнения можно найти, используя метод вариации постоянных. Пусть общее решение однородного дифференциального уравнения второго порядка имеет вид:
![]()
Вместо
постоянных C1
и C2
будем рассматривать вспомогательные
функции C1(x)
и C2(x).
Будем искать эти функции такими, чтобы
решение
![]()
удовлетворяло неоднородному уравнению с правой частью f(x). Неизвестные функции C1(x) и C2(x) определяются из системы двух уравнений:
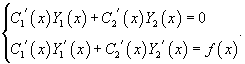
22. Числовой ряд. Сходимость и сумма ряда. Свойства сходящихся числовых рядов. Необходимое условие сходимости ряда.
Пусть мы имеем числовую последовательность а1,а2,а3,…аn…, где акϵR, к=1,2,3…
Числовой
ряд- это сумма членов числовой
последовательности вида

Частичная сумма числового ряда – это сумма вида Sn=a1+a2+…+an где n-некоторое натуральное число, наз-ют так же n-ой частичной суммой числового ряда.
Частичные суммы S1,S2,…Sn образуют бесконечную последовательность частичных сумм числового ряда.
Sn=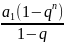 -Сумма убывающей геометрической
прогрессии.
-Сумма убывающей геометрической
прогрессии.
Числовой
ряд наз-ся сходящимся,
если существует конечный предел
последовательности частичных сумм S=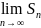
Если предел последовательности частичных сумм числового ряда не существует или бесконечен, то ряд наз-ся расходящимся.
Суммой сходящегося числового ряда наз-ся предел последовательности его частичных сумм,т.е.

Свойства сходящихся числовых рядов:
Если сходится числовой ряд
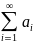 , то сходящимся будет и ряд
, то сходящимся будет и ряд
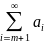
Если сходится числовой ряд и его сумма=S, то сходящимся будет и ряд
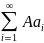 , причем
=AS,
где А-произвольная постоянная.
, причем
=AS,
где А-произвольная постоянная.Если сходятся числовые ряды и
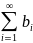 , их суммы равны A
и B
соответственно, то сходящимися будут
ряды
, их суммы равны A
и B
соответственно, то сходящимися будут
ряды
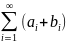 и
и
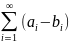 , причем их суммы будут равны A+B
и A-B
соответственно.
, причем их суммы будут равны A+B
и A-B
соответственно.
Необходимое условие сходимости ряда.
Если
числовой ряд сходится, то предел его
n-го
члена=0: