17. Понятие о дифференциальном уравнении: его порядке, общем и частном решении.

Обыкновенным дифференциальным уравнением наз-ся уравнение, связывающее искомую функцию, переменную и производные различных порядков данной функции.

В общем случае дифференциальное уравнение можно записать так G(x,y,y`,…,y⁽ⁿ⁾)=0 (1), где G- некоторая ф-ия n+2 переменных (n˃0), при этом n-порядок старшей производной, входящей в запись, наз-ся порядком дифференциального уравнения.

ПР:: x²y```-xy`=0 Обыкновенное диф-ое ур-ие третьего порядка.

Дифференциальное уравнение n-го порядка наз-ся разрешенным относительно старшей производной, если оно имеет вид:

y⁽ⁿ⁾=F(x,y,y`,…y^n-1) , где F – некоторая ф-ия n+1 переменной.

Решением диф-го ур-ия (1) наз-ся такая ф-ия у=у(х), кот. при подстановке её в это ур-ие обращает его в тождество.

Пр: ф-ия у=sinx яв-ся решением уравнения у```+у` =0, т.к. (sinx)```+(sinx)`=0 для любых х

Задача о нахождении решения некоторого дифференциального уравнения наз-ся задачей интегрирования данного диф-го уравнения.

График решения дифференциального уравнения наз-ся интегральной кривой.

ОБЩИМ РЕШЕНИЕМ диф-го ур-ия (1) n-го порядка наз-ся такое его решение y=φ(Х_j C1,…C_n), кот. яв-ся функцией переменной х и произвольных постоянных С₁,С₂,…С_n

ЧАСТНЫМ РЕШЕНИЕМ диф-го ур-ия наз-ся решение, кот. получено из общего решения, при некоторых конкретных числовых значениях постоянных С₁, С₂, … С_n

18. Дифференциальные уравнения первого порядка: с разделяющимися переменными.

Обыкновенное дифференциальное уравнение 1-го порядка (n=1) имеет вид: 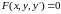или, если его удается разрешить относительно производной: . Общее решение y=y(x,С) или общий интеграл уравнения 1-го порядка содержат одну произвольную постоянную. Единственное начальное условие для уравнения 1-го порядка 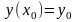позволяет определить значение константы из общего решения или из общего интеграла. Таким образом, будет найдено частное решение или, что тоже, будет решена задача Коши. Вопрос о существовании и единственности решения задачи Коши является одним из центральных в общей теории обыкновенных дифференциальных уравнений. Для уравнения 1-го порядка, в частности, справедлива теорема, принимаемая здесь без доказательства.

Определение. Дифференциальным уравнением с разделяющимися переменными называется уравнение вида

или уравнение вида

19. Линейные дифференциальные уравнения, однородные и неоднородные. Понятие общего решения линейного уравнения.

В математике линейное дифференциальное уравнение имеет вид

где дифференциальный оператор L линеен, y — неизвестная функция , а правая часть  — функция от той же переменной, что и y.

Линейный оператор L можно рассматривать в форме

Дифференциальное уравнение является однородным, если оно не содержит свободного члена — слагаемого, не зависящего от неизвестной функции. Так, можно говорить, что уравнение  — однородно, если .

В случае, если , говорят о неоднородном дифференциальном уравнении.

Неоднородное дифференциальное уравнение — дифференциальное уравнение (обыкновенное или в частных производных), которое содержит не равный тождественно нулю свободный член — слагаемое, не зависящее от неизвестных функций.

Общее решение диффференциального уравнения выражается в виде:

где C − произвольная постоянная.