12. Неопределенный интеграл, основные теоремы.
Теорема: Если ф-ия F(х) яв-ся первообразной ф-ии f(x) на промежутке Х, то всякая другая первообразная для ф-ии f(x) отличается от F(х) на постоянное слагаемое, т.е. может быть представлена в виде: F(х)+С, где С- произвольная постоянная
Совокупность всех первообразных для функции f(x) на промежутке Хназ-ся неопределённым интегралом от ф-ии f(х) и обозначается:
, где
,
f(х)-подынтегральная
ф-ия, f(x)dx-подынтегральное
выражение.
Свойства неопределённого интеграла:
Производная от неопределённого интеграла равна подынтегральной функции, т.е.
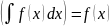
Дифференциал неопределённого интеграла равен подынтегральному выражению,т.е.
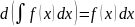
Неопределённый интеграл дифференциала некоторой функции равен этой функции с точностью до постоянного слагаемого,т.е.
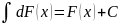
Неопределённый интеграл от алгеброической суммы конечного числа ф-ий равен такой же сумме неопределённых интегралов от этих ф-ий, т.е.
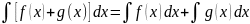
Постоянный
множитель можно выносить за знак
неопределённого интеграла,т.е.
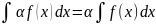
13.Интегрирование подстановкой.
Метод интегрирования подстановкой заключается во введении новой переменной интегрирования (то есть подстановки). При этом заданный интеграл приводится к новому интегралу, который является табличным или к нему сводящимся. Общих методов подбора подстановок не существует. Умение правильно определить подстановку приобретается практикой.
14. Интегрирование по частям.
Пусть
и(х)
и v(x)
- две функции от х, имеющие непрерывные
производные, тогда справедлива следующая
формула:
.
Эта формула называется формулой
интегрирования по частям и позволяет
свести данный интеграл более простому.
Пример:
=
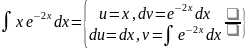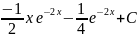
15. Интегрирование рациональных функций.
Задача интегрирования сводится к интегрированию простейших дробей следующих 4х типов:
,
,
,
.
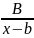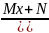Здесь
=2,3,…
λ=2,3…., В,М, N,
b.p,q
– некоторые вещественные числа, причем
трехчлен х2+рх+q
не имеет вещественных корней т.е. q
>0.
Из этого следует след. теорема
Теорема: Всякая рациональная дробь интегрируема в элементарных функциях.
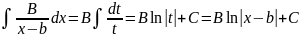
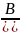
16. Определенный интеграл, основные теоремы.
Определённым
интегралом от непрерывной функции f(x)
на конечном отрезке [a, b]
(где 
)
называется приращение какой-нибудь её
первообразной на этом отрезке. При этом
употребляется запись
Числа a и b называются соответственно нижним и верхним пределами интегрирования, а отрезок [a, b] – отрезком интегрирования.
Основные теоремы:
Теорема. Определенный интеграл от непрерывной функции равен разности значений любой ее первообразной, вычисленных для верхнего и нижнего пределов интегрирования:
Формула Ньютона-Лейбница:
Пусть функция f (x) непрерывна на [a; b], а F (x) – какая-либо первообразная функции f на этом отрезке. Тогда
|
Таким образом, для вычисления определенного интеграла нужно найти какую-либо первообразную F функции f, вычислить ее значения в точках a и b и найти разностьF (b) – F (a).
Св-ва:
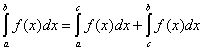
Если m≤f(x)≤M, то m(b-a)≤
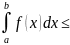M(b-a)