
- •Квадратный корень, функция
- •2.Предел функции.
- •3.Основные теоремы о пределах.
- •4.Непрерывность функции в точке и на интервале.
- •5.Производная и дифференциал.
- •6. Основные теоремы о дифференцируемых функциях
- •7.Функции нескольких переменных и их непрерывность.
- •8. Производные функции нескольких переменных
- •9. Дифференциалы функции нескольких переменных.
- •10. Поиск экстремума функции одной переменной.
- •11. Поиск экстремума функции двух переменных.
- •12. Неопределенный интеграл, основные теоремы.
- •Свойства неопределённого интеграла:
- •13.Интегрирование подстановкой.
- •15. Интегрирование рациональных функций.
- •16. Определенный интеграл, основные теоремы.
- •17. Понятие о дифференциальном уравнении: его порядке, общем и частном решении.
- •18. Дифференциальные уравнения первого порядка: с разделяющимися переменными.
- •19. Линейные дифференциальные уравнения, однородные и неоднородные. Понятие общего решения линейного уравнения.
- •20. Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами.
- •21. Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами. Метод Лагранжа вариации произвольных постоянных.
- •22. Числовой ряд. Сходимость и сумма ряда. Свойства сходящихся числовых рядов. Необходимое условие сходимости ряда.
- •23.Предельный признак сравнения. Признак Даламбера.
- •24.Знакопеременный ряд. Абсолютная и условная сходимость.
- •25.Степенные ряды. Теорема Абеля.
- •26. Разложение функций в степенные ряды. Ряд Тейлора.
- •27. Функции спроса и предложения.
- •28.Функция полезности. Кривые безразличия.
1 .Графики
и свойства основных элементарных
функций.
.Графики
и свойства основных элементарных
функций.
Квадратный корень, функция
Свойства:
1)
Область определения:
![]() =
[
=
[![]() )
2)
Область значений:
)
2)
Область значений:
![]() =
[
)
3)
Промежуток возрастания:[
)
4)
Промежутки убывания: нет
5)
Нули функции:
=
[
)
3)
Промежуток возрастания:[
)
4)
Промежутки убывания: нет
5)
Нули функции:
![]() 6)
Промежутки знакопостоянства:y>0 если
6)
Промежутки знакопостоянства:y>0 если
![]() (
);
y<0,
нет таких Х
(
);
y<0,
нет таких Х
2 )
Показательная функция
)
Показательная функция
![]() ,
где
a > 1
Свойства:
1)
Область определения:
=
(
,
где
a > 1
Свойства:
1)
Область определения:
=
(![]() )
2)
Область значений:
=
(
)
3)
Промежуток возрастания:(
)
4)
Промежутки убывания: нет
5)
Нули функции: нет
6)
Промежутки знакопостоянства:y>0 если
(
);y<0,
нет таких Х
)
2)
Область значений:
=
(
)
3)
Промежуток возрастания:(
)
4)
Промежутки убывания: нет
5)
Нули функции: нет
6)
Промежутки знакопостоянства:y>0 если
(
);y<0,
нет таких Х
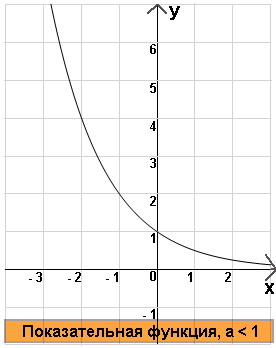
3)Показательная функция , где a < 1 Свойства: 1) Область определения: = ( ) 2) Область значений: = ( ) 3) Промежутки возрастания: нет 4) Промежуток убывания:( ) 5) Нули функции: нет 6) Промежутки знакопостоянства:y>0 если ( );y<0, нет таких Х
4 )Логарифмическая
функция
)Логарифмическая
функция
![]() ,
a > 1
Свойства:
1)
Область определения:
=
(
)
2)
Область значений:
=
(
)
3)
Промежуток возрастания:
(
)
4)
Промежуток убывания: нет
5)
Нули функции: x=1
6)
Промежутки знакопостоянства:y>0
если
(
,
a > 1
Свойства:
1)
Область определения:
=
(
)
2)
Область значений:
=
(
)
3)
Промежуток возрастания:
(
)
4)
Промежуток убывания: нет
5)
Нули функции: x=1
6)
Промежутки знакопостоянства:y>0
если
(![]() );y<0
если
(
);y<0
если
(![]() )
)
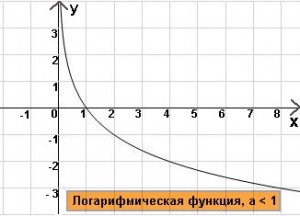 5)Логарифмическая
функция
,
a < 1
Свойства:
1)
Область определения:
=
(
)
2)
Область значений:
=(
)
3)
Промежуток возрастания: нет
4)
Промежуток убывания:(
)
5)
Нули функции: x=1
6)
Промежутки знакопостоянства:y>0 если
(
);y<0
если
(
)
5)Логарифмическая
функция
,
a < 1
Свойства:
1)
Область определения:
=
(
)
2)
Область значений:
=(
)
3)
Промежуток возрастания: нет
4)
Промежуток убывания:(
)
5)
Нули функции: x=1
6)
Промежутки знакопостоянства:y>0 если
(
);y<0
если
(
)
6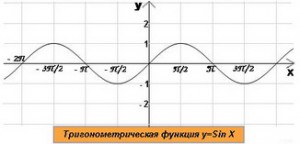 )Тригонометрическая
функция
)Тригонометрическая
функция
![]() Свойства:
1)
Область определения:
=(
)
2)
Область значений:
=[
Свойства:
1)
Область определения:
=(
)
2)
Область значений:
=[![]() ]
3)
Промежутки возрастания:
[
]
3)
Промежутки возрастания:
[![]() ],
где
],
где
![]() 4)
Промежутки убывания: [
4)
Промежутки убывания: [![]() ],
где
5)
Нули функции:
],
где
5)
Нули функции:
![]() ,
где
6)
Промежутки знакопостоянства:y>0 если
[
,
где
6)
Промежутки знакопостоянства:y>0 если
[
![]() ],
где
y<0 если
[
],
где
y<0 если
[
![]() ],
где
],
где
7 )Тригонометрическая
функция
)Тригонометрическая
функция
![]() Свойства:
1)
Область определения:
=(
)
2)
Область значений:
=[
]
3)
Промежутки возрастания: [
],
где
4)
Промежутки убывания:
[
],
где
5)
Нули функции:
Свойства:
1)
Область определения:
=(
)
2)
Область значений:
=[
]
3)
Промежутки возрастания: [
],
где
4)
Промежутки убывания:
[
],
где
5)
Нули функции:
![]() ,
где
6)
Промежутки знакопостоянства:
,
где
6)
Промежутки знакопостоянства:
y>0
если
[
![]() ],
где
y<0 если
[
],
где
],
где
y<0 если
[
],
где
2.Предел функции.
Предел функции в точке:
Число А наз-ся пределом ф-ии у=f (x) при х стремящемся к х0, если для любого даже сколь угодно малого положительного числа Е найдётся такое положительное число I (зависящее от Е) что для всех х неравных х0 и удовлетворяющих условию ǀх - х0ǀ < I верно неравенство ǀf (x) - Aǀ<E
Этот
предел ф-ии обознач-ся:
 =A
=A
Предел функции в бесконечности:
Число А наз-ся пределом ф-ии у=f(x) при х, стремящемся к бесконечности, если для любого даже сколь угодно малого положительного числа Е найдётся такое положительное число S (зависящее от Е) что для всех х таких, что ǀхǀ˃S верно нер-во: ǀf(x) – A ǀ<E
Этот предел ф-ии обознач-ся:

3.Основные теоремы о пределах.
Т1. Функция не может иметь более одного предела
Т2.
Предел алгебраической суммы конечного
числа функции равен такой же сумме
пределов этих функций, т.е.

Т3. Предел произведения конечного числа фун-ий равен произведению пределов этих ф-ий.
10 Постоянный множитель можно выносить за знак предела, т.е.

Т4. Предел частного двух ф-ий равен частному этих двух ф-ий при условии, что предел делителя не равен нулю, т.е.

20 Предел степени равен степени пределов ,т.е.

