Эквивалентные преобразования последовательного, параллельного и смешанного соединений с r-элементами

Последовательное соединение резисторов. При рассмотрении электрических цепей при последовательном соединении сопротивлений (конец первого сопротивления соединяется с началом второго и т. д.) следует усвоить расчет эквивалентного сопротивления цепи, напряжения на сопротивлениях, тока и мощности цепи.

На рисунке показана простая электрическая схема с последовательным соединением элементов.

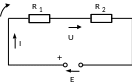
Электрическая схема с последовательным соединением резисторов

Применив II ЗК для цепи, определим эквивалентное сопротивление

IR₁ + IR₂ = Е,

откуда

U₁ + U₂ = Е,

или

U₁ + U₂ = U;

I(R₁ + R₂) = U;

IR_экв = U,

где

R_экв = R₁ + R₂.

Следовательно, при последовательном соединении элементов:

- эквивалентное сопротивление цепи равно сумме сопротивлений:

R_экв = R₁ + R₂,

- падения напряжения на последовательно соединенных сопротивлениях пропорциональны величинам сопротивлений:

U₁ = IR₁; U₂ = IR₂;

- сумма падений напряжений на сопротивлениях равна U, В, напряжению на зажимах цепи:

U = U₁ + U₂;

- ток цепи I, А определяется по формуле:

I = Е/R_экв;

- активная мощность цепи Р, Вт:

Р = RI ² .

Таким образом, падения напряжения на последовательно соединенных сопротивлениях пропорциональны величинам сопротивлений, сумма падений напряжений на сопротивлениях равна напряжению на зажимах последовательной цепи, а эквивалентное сопротивление цепи равно сумме последовательно соединенных сопротивлений.

При последовательном соединении сопротивлений по всем элементам цепи протекает один и тот же ток.

Параллельное соединение резисторов. При изучении электрических цепей при параллельном соединении сопротивлений (начала всех сопротивлений соединены вместе и концы соединены вместе) необходимо правильно определять эквивалентное сопротивление цепи, эквивалентную проводимость, токи всех ветвей.

Схема параллельного соединения элементов.

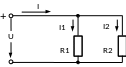
Электрическая схема с параллельным соединением резисторов

На этой схеме для упрощения расчета вместо ЭДС E источника питания указано напряжение U на зажимах источника питания.

Согласно закону Ома, токи I₁ и I₂, А, в ветвях 1 и 2 равны

I₁ = U/R₁, I₂ = U/R₂.

Ток I, протекающий по неразветвленному участку цепи, можно определить по I ЗК:

I = I₁+ I₂, или I = U/R_экв.

Для определения эквивалентного сопротивления запишем токи I, I₁, I₂, выразив их через напряжения, сопротивления или проводимости:

U/R_экв = U/R₁ + U/R₂; UG_экв = UG₁ + UG₂,

где G – проводимость элемента цепи.

Эквивалентная проводимость цепи G_экв, См: Сименс, единица измерения проводимости.

G_экв = 1/R_экв; G₁ = 1/R₁; G₂ = 1/R₂

Тогда

1/R_экв = 1/R₁ + 1/R₂,

R_экв = R₁R₂ /(R₁+R₂).

Следовательно, при параллельном соединении сопротивлений:

- токи в ветвях распределяются прямо пропорционально напряжению и обратно пропорционально сопротивлениям этих ветвей или прямо пропорционально их проводимостям:

I₁ = U/R₁, I₂ = U/R₂,

I₁ = UG₁, I₂ = UG₂;

где G₁, G₂ - проводимости ветвей цепи, См:

G₁ = 1/R₁, G₂ = 1/R₂;

- ток I, А, в неразветвленной части цепи равен сумме токов параллельных ветвей:

I = I₁ + I₂;

- эквивалентная проводимость G_экв, См, параллельного соединения сопротивлений равна сумме проводимостей параллельных ветвей:

G_экв = G₁ + G₂;

- эквивалентное сопротивление цепи R_экв, Ом:

R_экв = R₁ R₂/(R₁ + R₂);

- активная мощность цепи Р, Вт:

Р = R_эквI².

Таким образом, токи в параллельно соединенных ветвях распределяются обратно пропорционально сопротивлениям этих ветвей или прямо пропорционально их проводимостям. Ток в неразветвленной части цепи равен сумме токов параллельных ветвей, а эквивалентная проводимость параллельного соединения равна сумме проводимостей параллельных ветвей.

При параллельном соединении сопротивлений напряжения на элементах схемы одинаковы.

Смешанное соединение резисторов. При смешанном соединении сопротивлений электрическая цепь содержит участки цепи, как с параллельным, так и с последовательным соединением элементов цепи, для расчета цепи необходимо изучить метод свертывания электрических цепей.

Схема данного соединения сопротивлений приведена на рисунках.

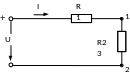
а б

Схемы электрических цепей:

а - со смешанным соединением сопротивлений; б – преобразованная

При расчете цепи со смешанным соединением сопротивлений используют метод эквивалентных преобразований, определяя:

- проводимость разветвленных участков G₂₃, См (находят как сумму проводимостей параллельных ветвей):

G₂₃ = G₂ + G₃;

- эквивалентное сопротивление этого же участка цепи R₂₃, Ом:

R₂₃ = R₂ R₃/(R₂ + R₃);

- последовательно соединенные сопротивления (рис.1.6, б) суммируют, определяя R_экв, Ом:

R_экв = R₁ + R₂₃;

- ток, протекающий по неразветвленному участку цепи I₁, А:

I₁ = U/R_экв, или I₁ = G_эквU;

- напряжение параллельных ветвей U₂₃, В:

U₂₃ = IR₂₃,

- токи ветвей I₂, I₃, А:

I₂ = U₂₃/R₂; I₃ = U₂₃/R₃;

- активную мощность цепи Р, Вт:

Р = R_эквI₁².

Таким образом, при расчете цепи со смешанным соединением сопротивлений пользуются методом эквивалентных преобразований схемы. При этом проводимость разветвленных участков находят как сумму проводимостей параллельных ветвей или эквивалентное сопротивление параллельно соединенных ветвей, а затем последовательно соединенные сопротивления суммируют.

В цепи с одним источником направление тока всегда известно – от положительной клеммы источника питания. Как видим из приведенных схем, расчет простых цепей ведется методом эквивалентных преобразований.