
- •23) Интерференция света. Интерференционная картина от двух источников.
- •24)Дифракция света. Метод зон Френеля. Прямолинейное распространение света.
- •25) Дифракция Френеля на круглом отверстии и на диске.
- •26) Дифракция Фраунгофера на одной щели. Дифракция Фраунгофера на дифракционной решетке.
- •27) Дифракция на пространственной решетке. Дифракция рентгеновских лучей. Формула Вульфа – Брегов.
- •28)Понятие о голографии.
25) Дифракция Френеля на круглом отверстии и на диске.
Рассмотрим случай прохождения света от точечного источника I через круглое отверстие. На рис. 2.2. изображен сферический фронт волны S на границе отверстия АВ. Для определения освещенности в точке P, взятой в центре экрана, разделим фронт S на кольцевые участки – зоны Френеля. Деление произведем так, чтобы оптические пути от точки P до краев двух соседних зон отличались на λ/2, т.е. из точки P как из центра проведем концентрические сферы радиусами:
г де
n
– любое число. Расчет показывает, что
площади зон Френеля приблизительно
одинаковы, и, следовательно, число
вторичных источников света во всех
зонах также примерно одинаково. С
увеличением номера зоны (1, 2, 3, ...)
расстояние от нее до точки P
увеличивается, и поэтому амплитуды
колебаний, приходящих в точку наблюдения
от различных зон, монотонно убывают:
де
n
– любое число. Расчет показывает, что
площади зон Френеля приблизительно
одинаковы, и, следовательно, число
вторичных источников света во всех
зонах также примерно одинаково. С
увеличением номера зоны (1, 2, 3, ...)
расстояние от нее до точки P
увеличивается, и поэтому амплитуды
колебаний, приходящих в точку наблюдения
от различных зон, монотонно убывают:
![]() (2)
(2)
Так как колебания от двух соседних зон приходят в точку P в противо-фазах, то амплитуду суммарного колебания можно записать следующим образом:
А =А1-А2+А3-А4+…±Аm.
(3)
=А1-А2+А3-А4+…±Аm.
(3)
Разобьем все нечетные члены в правой части равенства 3 на два слагаемых:
 т.е.,
если число зон m,
укладывающихся в отверстии АВ, четное,
то в точке P
будет минимум освещенности, а если –
нечетное, то – максимум освещенности.
Для нахождения числа зон Френеля m
выполним вспомогательные построения
к рис. 2.2 (см. рис. 2.3). Из точек I
и P
как из центров опишем сферы, проходящие
через край отверстия АВ. Пусть d
– диаметр отверстия АВ, a
и b
– расстояния от центра отверстия D
до точек I
и P.
т.е.,
если число зон m,
укладывающихся в отверстии АВ, четное,
то в точке P
будет минимум освещенности, а если –
нечетное, то – максимум освещенности.
Для нахождения числа зон Френеля m
выполним вспомогательные построения
к рис. 2.2 (см. рис. 2.3). Из точек I
и P
как из центров опишем сферы, проходящие
через край отверстия АВ. Пусть d
– диаметр отверстия АВ, a
и b
– расстояния от центра отверстия D
до точек I
и P.![]()
Поэтому
для определения числа m
необходимо знать величину отрезка
СО=m .
.
В прямоугольнике LAO:


В прямоугольнике CAK:
![]()
Пренебрегая
малыми величинами в (2.9, а, б)
![]() ,
получаем
,
получаем и с учетом СО=m
.
имеем:
и с учетом СО=m
.
имеем:
На рис. 2.4 приводится примерный вид распределения интенсивности света на плоскости экрана для различных значений числа зон m, наблюдаемых из его центра P.

26) Дифракция Фраунгофера на одной щели. Дифракция Фраунгофера на дифракционной решетке.
П
 ри
дифракции параллельного пучка световых
лучей на узкой щели фронт падающей волны
( в пределах щели) можно считать плоским
(рис. 2.1, б). Рассмотрим дифракционную
картину на экране MN,
удаленном от щели в бесконечность. При
этом следует учитывать, что параллельные
пучки световых лучей от вторичных
источников в бесконечности соберутся
в отдельные точки. (При близко расположенном
экране параллельные пучки можно собрать
с помощью линзы). Следовательно, для
расчета результата интерференции
вторичных волн достаточно рассмотреть
фазовые соотношения между лучами в
параллельных пучках. Один из этих пучков
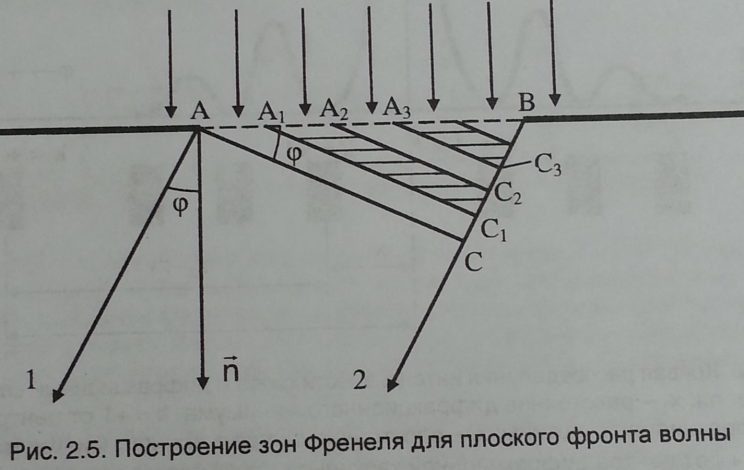
изображен на рис. 2.5.Обозначим через φ
угол между нормалью к плоскости щели n
и направлением лучей. Опустим перпендикуляр
АС на луч 2. Полученную разность хода BC
между крайними лучами 1 и 2 разделим на
отрезки длиной
ри
дифракции параллельного пучка световых
лучей на узкой щели фронт падающей волны
( в пределах щели) можно считать плоским
(рис. 2.1, б). Рассмотрим дифракционную
картину на экране MN,
удаленном от щели в бесконечность. При
этом следует учитывать, что параллельные
пучки световых лучей от вторичных
источников в бесконечности соберутся
в отдельные точки. (При близко расположенном
экране параллельные пучки можно собрать
с помощью линзы). Следовательно, для
расчета результата интерференции
вторичных волн достаточно рассмотреть
фазовые соотношения между лучами в
параллельных пучках. Один из этих пучков
изображен на рис. 2.5.Обозначим через φ
угол между нормалью к плоскости щели n
и направлением лучей. Опустим перпендикуляр
АС на луч 2. Полученную разность хода BC
между крайними лучами 1 и 2 разделим на
отрезки длиной![]() и проведем через точки деления линии,
параллельные АС. В результате построений
фронт волны в щели AB
разобьется на ряд зон (АА1,
А1А2,
А2А3,
…).
Лучи от соседних зон приходят на экран
в противофазе, поэтому количество зон
определяет результат интерференции
пучка световых лучей. Как видно из рис.
2.5, число зон
и проведем через точки деления линии,
параллельные АС. В результате построений
фронт волны в щели AB
разобьется на ряд зон (АА1,
А1А2,
А2А3,
…).
Лучи от соседних зон приходят на экран
в противофазе, поэтому количество зон
определяет результат интерференции
пучка световых лучей. Как видно из рис.
2.5, число зон
 .
.
 где
δ = АВ – ширина щели. Таким образом, от
выбора угла φ зависит число зон m
и, следовательно, результат интерференции.
На рис. 2.6 представлен примерный вид
распределения интенсивности
дифрагированного на щели света и
дифракционный спектр, наблюдаемый на
экране MN.
где
δ = АВ – ширина щели. Таким образом, от
выбора угла φ зависит число зон m
и, следовательно, результат интерференции.
На рис. 2.6 представлен примерный вид
распределения интенсивности
дифрагированного на щели света и
дифракционный спектр, наблюдаемый на
экране MN.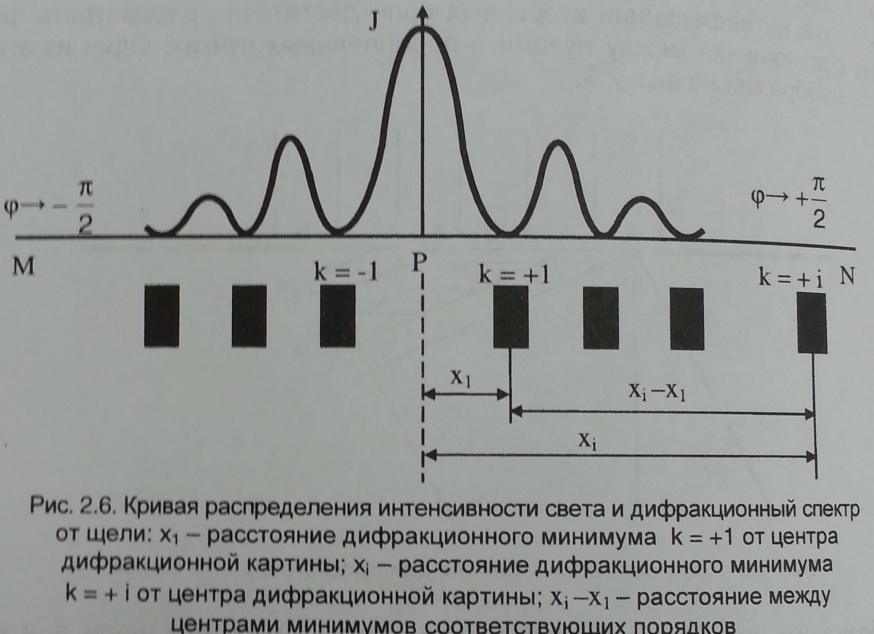
Если
углы φ соответствуют четному числу зон
m
= 2k,
то в этих направлениях наблюдаются
минимумы освещенности![]()
Для
углов, соответствующих
![]() наблюдаются
максимумы освещенности
наблюдаются
максимумы освещенности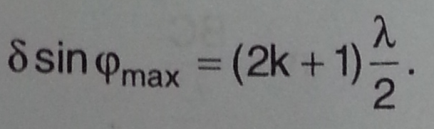
Т.к.
при дифракции волны от вторичных
источников (рис. 2.5) распространяются
во всех направлениях от
![]() то
на экране минимумы и максимумы чередуются,
располагаясь симметрично относительно
центрального (нулевого) максимума (φ=0).
С учетом того, что высота щели значительно
больше ее ширины, дифракционная картина
на экране будет представлять ряд
чередующихся светлых и темных полос.
то
на экране минимумы и максимумы чередуются,
располагаясь симметрично относительно
центрального (нулевого) максимума (φ=0).
С учетом того, что высота щели значительно
больше ее ширины, дифракционная картина
на экране будет представлять ряд
чередующихся светлых и темных полос.
