3. Статистичне регулювання технологічних процесів. Методи серединних арифметичних значень та розмахів

(Анофрієв ст. 109-113)

Методи статистичного регулювання технологічних процесів (СРТП), по суті справи, являють собою методи поточного контролю за виробництвом і попередження браку шляхом своєчасного втручання в технологічний процес. Технічним допоміжним засобом СРТП є контрольні карти, що дозволяють наочно відбити хід виробничого процесу на графіку й таким чином виявити порушення технології. У залежності від призначення готової продукції і засобів її виготовлення застосовуються контрольні карти, що використовують методи:

• середніх арифметичних значень;

• розмахів;

• медіан;

• індивідуальних значень;

• контролю некількісних ознак.

Всі ці методи достатньо схожі і можуть бути розглянуті на прикладі найбільш поширеної на практиці контрольної карти середніх арифме­тичних значень х.

Техніка побудови і ведення карти х міститься в наступному.

Нехай у механічному цеху заводу виготовляються настановні кільця визначеного типу. Щоб перевірити, чи забезпечує верстат задані норми якості в окремих кільцях, визначають вимірну ознаку - товщину, номі­нальне значення котрої повинно дорівнювати а. Припустимі відхилена» від а складають . Якщо товщина кільця знаходиться в межах і , то воно відповідає нормам якості, якщо ні, то кільці вважається непридатним. Поле допуску складає

На початку виробництва верстат налагоджують на номінальний роз­мір. Надалі в ході процесу з'являються відхилення розмірів, обумовлені випадковими (вібрація верстата і т.п.) і систематичними (знос інструмента, нагрівання деталі і т.п.) помилками. Щоб проконтролювати, чи не випускається брак, через визначені, заздалегідь установлені відрізки час) із верстата знімають останні n випущених кілець, їх називають пробоїн або підгрупою, а не вибіркою, оскільки вона вибирається не випадковим чином, і в кожного кільця вимірюють товщину. Потім по отриманим n індивідуальним значенням за допомогою формули

розраховують середнє арифметичне значення і здійснюють перевірку статистичної гіпотези . Умовою застосування такого статистичного методу є те, що ознака х розподілена нормально з математичним сподіванки і дисперсією . Гіпотеза не відкидається (тобто верстат забезпечує нормальний розмір) поки х, розраховане по n індивідуальних значеннях, задовольняє нерівності:

визначається за таблицями на основі співвідношення

де - ймовірність похибки гіпотези .

У випадку порушення наведеного вище нерівності гіпотеза відки­дається. На практиці це означає, що верстат не забезпечує номінального розміру "а" внаслідок деяких неполадок, причину яких варто встановити і виконати підналагодження верстата.

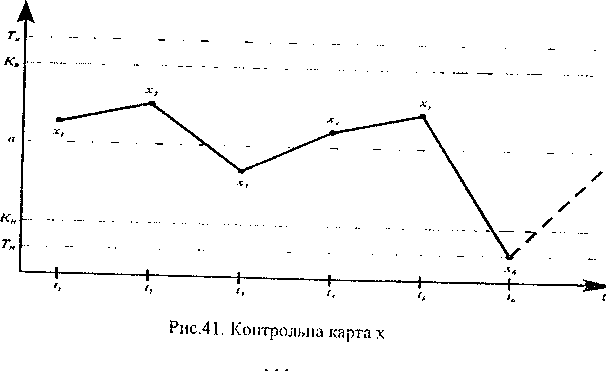
Використання даного методу стосовно до техніки побудови контроль­них карт виглядає таким чином. У прямокутній системі координат ( рис.41) викреслюють лінію а та межі області гіпотези .

По осі абсцис на рівних відстанях відкладають моменти часу відбору проб із n деталей а по осі ординат у відповідному масштабі задаються у виді точок значення . Такий графік називають контрольною картою. Доти, поки точки ламаної знаходяться усередині контрольних меж, верстат забезпечує номінальний розмір і процес стабі­льний. Якщо, крім того, не порушені межі допуску, він знаходиться в ста­тистично підконтрольному стані. Поява точки поза розцінює­ться як сигнал до припинення виробничого процесу і перевірки настрою­вання верстата. У даному випадку необхідно проконтролювати всі деталі, випущені в період між даною і попередньою пробою ї зробити розбраку­вання.

При побудові карти найважливішою задачею є розрахунок контрольних меж, що залежать від характеристики виробничого процесу - розміру а, дисперсії , а також можливості помилки і обсягу проби n. Значення а и n заздалегідь фіксуються, на практиці їх звичайно приймають рівними n = 4...7, а = 0,0027 = 0,27% (z = 3) або = 0,001 = 1% ( z_а = 2,576). В першому випадку ( = 0,27%) це означає, що усередині контрольних меж очікується поява 99,73% усіх значень спостережуваної ознаки , а у другому - 99% усіх значень, тобто при статистичному підконтрольному процесі майже всі значення лежать усередині контрольних межи. Крім а и n для розрахунку потрібно знати параметри нормально розподіленої генеральної сукупності. Звичайно а приймають рівною номінальному значенню ознаки, а дисперсія , якщо вона, як технологічна характеристика верстата невідома, визначається декількома способами, із котрих самим простим є метод оцінки за розмахом R:

Розрахунок виконують таким способом. Для кожної з проб( ) обсягом n знаходять розмахи і знаходять їх середнє арифметичне

У стандартній теорії оцінок показується, що математичне сподівання . Коефіцієнт залежить від обігу проби n і визначається за таблицями. Таким чином,

де

тобто ширина контрольного інтервалу при дорівнює :

З іншого боку, поле допуску контрольованого розміру визначається нерівностю

де , називають креслярським допуском. Чим вужче поле допуску, тим вище якість виробу, проте, вимоги до технічного оснащення процесу зростають. Так, якщо контрольні межі збігаються з полем допуску і процес стабільний, бракуються три деталі з тисячі. Якщо контрольні межі вужче креслярського допуску, то не виробляється майже ніякого браку, тобто має місце ідеальний випадок. Якщо ж вони ширше поля допуску, то може різко зрости відсоток браку, хоча процес і буде залишатися стабіль­ним. Високий відсоток браку може стати приводом до перегляду кресляр­ських допусків і приведенню їх у відповідність із точними показника­ми існуючого технологічного устаткування.