
Тема 7. Специальные вопросы финансового менеджмента
Цель практикума по данной теме — сформировать навык решения задач по управлению финансами предприятия в условиях инфляции, по оценке вероятности банкротства, ознакомить с подходами к оценке бизнеса. |
Методические указания
Приступая к рассмотрению примеров и самостоятельному решению задач, необходимо внимательно прочесть контент по соответствующему вопросу темы. Базовая концепция в данной теме — это концепция временной ценности денег, концепция компромисса между риском и доходностью. Важнейшие понятия: инфляция, уровень, темп и индекс инфляции, финансовое состояние, финансовая несостоятельность, банкротство, финансовая реструктуризация, стоимость предприятия, стоимость бизнеса. Эти понятия следует выучить и разобраться в их соотношениях.
Эта тема является завершающей. Поэтому здесь представлены задачи, затрагивающие вопросы предшествующих тем.
В решении задач используются формулы, объяснение которых представлено в контенте. Для облегчения поиска необходимых разъяснений в контенте нумерация формул и обозначения в практикуме такие же, как и в контенте.
7.1. Финансовый менеджмент в условиях инфляции
В данном параграфе используются следующие обозначения:
d — ставка доходности, %;
![]() —
минимальная
допустимая доходность, %;
—
минимальная
допустимая доходность, %;
![]() —
безрисковая
доходность, %;
—
безрисковая
доходность, %;
F (FV) — будущая (наращенная) стоимость, ден. ед.;
![]() -
индекс инфляции, %;
-
индекс инфляции, %;
P (PV) — настоящая (дисконтированная) стоимость, ден. ед.;
r — реальная ставка доходности, %;
![]() —
ставка
с учетом инфляции (номинальная), %;
—
ставка
с учетом инфляции (номинальная), %;
![]() —
минимально
допустимая доходность, %;
—
минимально
допустимая доходность, %;
![]() —
темп
инфляции, %;
—
темп
инфляции, %;
![]() V —
прирост стоимости (сумма полученных
процентов), ден. ед.
V —
прирост стоимости (сумма полученных
процентов), ден. ед.
В некоторых задачах вводятся дополнительные обозначения.
Задача 7.1.1.
Минимально необходимая доходность 12 % годовых. Темп инфляции 11 %. Какова должна быть номинальная ставка?
Методические указания: использовать формулу (7.1.10).
Дано: d = 0,12
____________
|
Решение: Ставка доходности играет роль ставки дисконтирования (d = r). Воспользуемся формулой Фишера (7.1.10):
|
Ответ: Номинальная ставка должна быть не ниже 24,32 %.
Задача 7.1.2.
Определить номинальную ставку процентов для финансовой операции, если уровень эффективности должен составлять 7 % годовых, а годовой уровень инфляции составляет 22 %.
Методические указания: использовать формулу (7.1.10).
Дано:
|
Решение: Номинальная ставка процентов определяется по формуле Фишера:
|
|
Ответ: Номинальная ставка составляет 30,54 % при реальной ставке 7 %.
Задача 7.1.3.
Вклады принимают под 14 %. Какова их реальная доходность при инфляции 11 %?
Методические указания: использовать формулу (7.1.10).
Дано:
_____________ d = ? |
Решение: Воспользуемся формулой Фишера (7.1.10), из которой следует:
|
Заметим, что реальная доходность меньше, чем простая разность процентной ставки и темпа инфляции:
![]()
Ответ: Реальная доходность составляет 2,7 %.
Задача 7.1.4.
Ожидаемый темп инфляции 2 % в месяц. Определить квартальный и годовой темп инфляции.
Методические указания: 1) использовать формулы (2.1.7) и (2.1.9);
2)
ввести обозначения:
![]() -
темп инфляции в месяц,
-
темп инфляции в месяц,
![]() -
темп инфляции в квартал,
-
темп инфляции в квартал,
![]() -
годовой темп инфляции.
-
годовой темп инфляции.
Дано:
|
Решение: Квартальный темп инфляции рассчитаем на основе формулы для нахождения эффективной ставки процента:
|
Годовой темп инфляции можно рассчитать двумя способами:
1) используя темп инфляции в месяц:
![]()
2) используя темп инфляции в квартал:
![]()
Ответ: Квартальный темп инфляции 6,12 %, годовой темп инфляции 26,82 %.
Задача 7.1.5.
Определить реальную доходность при размещении средств на год под 14 % годовых, если уровень инфляции за год составляет 10 %.
Методические указания: 1) использовать формулу (7.1.10).
Дано:
______________ r=? |
Решение: Формула пересчета реальной доходности:
|
Ответ: Реальная доходность составляет 3,63 % годовых.
Задача 7.1.6.
Клиент вкладывает в банк на год 20 тыс. р., инфляция составляет 18 %. Клиент хочет, чтобы его вклад принес 6 % годовых дохода. Под какой процент клиент должен сделать вклад?
Методические указания: использовать формулу (7.1.10).
Дано:
|
Решение: Годовая ставка сложных процентов, обеспечивающая реальную доходность кредитной операции, определяется по формуле Фишера:
|
Ответ: Чтобы получить годовой доход в размере 6 % годовых, ставка по кредиту с учетом инфляции должна быть не менее 25,08 %.
Задача 7.1.7.
Клиент вкладывает в банк на год 20 тыс. р. под 6 % годовых, инфляция составляет 18 %. Какой результат получит вкладчик от данной операции?
Методические указания: использовать формулы (2.1.1), (2.1.3) и (7.1.10).
Дано:
|
Решение: 1. Номинальная наращенная сумма (будущая стоимость):
2. Номинальные начисленные проценты:
Реальная наращенная сумма: |
V = ? |

3. Реальные проценты:
![]()
Ответ: Номинально (счетно) клиент получает 1200 р. дополнительно к своим 20 тыс. р. Однако обесценивание денег в результате инфляции приводит к тому, что реальная ценность полученной суммы меньше вложенной на 2033,9 р.
Задача 7.1.8.
Темпы инфляции в ближайшие 5 лет прогнозируются по годам следующим образом: 14 %, 12 %, 8 %, 7 %, 5 %. Как изменятся цены за пятилетие?
Методические указания: 1) использовать формулы (7.1.5) и (7.1.6);
2)
ввести обозначения:
![]() -
темп инфляции в t -м году,
-
темп инфляции в t -м году,
![]() -
индекс цен в t -м году,
-
индекс цен в t -м году,
![]() -
индекс цен за n лет;
-
индекс цен за n лет;
![]() -
среднегодовое значение индекса за n лет;
-
среднегодовое значение индекса за n лет;
![]() -
средний
однодневный темп изменения цен.
-
средний
однодневный темп изменения цен.
Дано: Т1 = 0,14 Т2 = 0,12 Т3 = 0,08 Т4 = 0,07 Т5 = 0,05 ____________
|
Решение: Индекс цен за 5 лет рассчитывается как произведение годовых индексов:
Таким образом, за пятилетие цены возрастут в 1,55 раза, или на 55 % (для сравнения рассчитаем простую сумму темпов инфляции, которая оказывается существенно ниже рассчитанной: 14 + 12 + 8 + 7 + 5 = 46 < 55). |
Найдем среднегодовой за пятилетие темп инфляции:
![]() ,
т. е. среднегодовой темп инфляции
равен:
,
т. е. среднегодовой темп инфляции
равен:
1 — 1,0916 = 0,0916 = 9,16 %.
Найдем среднедневный за 5 лет темп инфляции:
![]() ,
т. е. среднедневный темп инфляции равен
0,024 %.
,
т. е. среднедневный темп инфляции равен
0,024 %.
Найдем среднедневный темп инфляции во 2-м году анализируемого пятилетия:
![]() ,
т. е. среднедневный темп инфляции во 2-м
году равен 0,031 %.
,
т. е. среднедневный темп инфляции во 2-м
году равен 0,031 %.
Ответ: За пятилетие цены возрастут в 1,55 раза или на 55 %, при этом среднегодовой темп роста цен составит 9,16 %, среднедневный темп — 0,024 %.
Задача 7.1.9.
Существует проект, в который требуется вложить 20 млн руб. Минимально допустимая доходность 5 % в год. Доход от реализации проекта будет получен через 2 года в объеме 26 млн руб. Безрисковая норма доходности - 8 % в год. Бета-коэффициент равен 0,9. Ожидаемый темп инфляции - 10 %. Среднерыночная норма доходности по аналогичным проектам 18 % годовых.
Следует ли принять данный проект?
Методические указания: 1) использовать формулы (2.1.7), (2.5.13) и (7.1.8);
2)
ввести обозначения: n — срок реализации
проекта,
![]() -
бета-коэффициент,
-
бета-коэффициент,
![]() -
средняя рыночная доходность,
-
средняя рыночная доходность,
![]() -
номинальная доходность проекта, d —
реальная доходность проекта,
-
номинальная доходность проекта, d —
реальная доходность проекта,
![]() -
премия за риск,
-
премия за риск,
![]() -
максимально приемлемые вложения,
-
максимально приемлемые вложения,
![]() -
доходность с учетом инфляции,
-
доходность с учетом инфляции,
![]() -
минимальный приемлемый доход.
-
минимальный приемлемый доход.
Дано: P = 20 млн руб.
F = 26 млн руб.
Принять проект? |
Решение: Номинальная доходность проекта составляет:
Оценку целесообразности реализации проекта можно осуществить тремя способами:
Рассмотрим эти способы. |
Первый способ. Для нахождения реальной доходности проекта воспользуемся формулой определения будущей стоимости (2.1.7) с учетом инфляции (7.1.8) и риска (2.5.13):
![]() (*)
(*)
Преобразуя эту формулу, получаем:
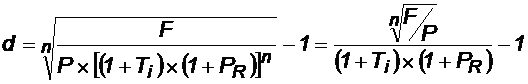 .
.
Для расчета d необходимо предварительно рассчитать премию за риск (формула 2.5.13):

Реальная доходность не только меньше минимально допустимой, но и в целом данный проект относительно убыточен, поэтому его реализация не целесообразна.
Второй способ. Исходя из формулы (*), определим максимально приемлемые вложения:

Полученный результат означает, что проект не приемлем в случае доступности вложений на рынке.
Если не брать в расчет условия вложений на рынке (среднюю доходность, риск), а учесть только инфляцию, то доходность проекта составит:

И в этом случае ожидаемая доходность меньше минимально допустимой, т. е. проект неприемлем.
Третий способ. Исходя из среднерыночных условий и суммы вложений, рассчитаем минимально приемлемый доход и сравним его с ожидаемым.
Приемлемый доход (ф.(*)) при вложении 20 млн р. составит:
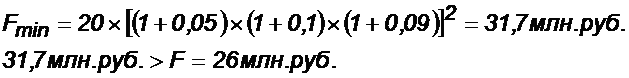
Данный результат еще раз подтверждает сделанный вывод о неприемлемости рассматриваемого проекта.
Ответ: Проект неприемлем.
Задача 7.1.10.
Можно купить пакет бескупонных облигаций за 9 тыс. р. Срок погашения облигаций - 2 года. Номинальная цена пакета 12 тыс. р. Ожидаемый темп инфляции 10 %. Стоит ли купить пакет облигаций, если нужен реальный доход не менее 4 % годовых?
Методические указания: 1) использовать формулы (2.1.7) и (7.1.10);
2) ввести обозначения: P — настоящая стоимость пакета облигаций, n — срок погашения облигаций, N — номинал пакета облигаций.
Дано: P=9 тыс. р. N =12 тыс. р.
_______________ r — ? |
Решение:
Найдем
|
Далее воспользуемся формулой Фишера (7.1.10):

Ответ: Пакет облигаций следует приобрести, т. к. его реальная доходность выше минимально допустимой.
Задача 7.1.11.
Инвестор вкладывает на 3 года в объект инвестирования 1 млн.руб. Требуемая реальная процентная ставка доходности 5 % в год. Прогнозируемый среднегодовой темп инфляции 10 %. Определить минимальную сумму денежных средств, которую должен принести инвестору данный объект инвестирования, чтобы инвестору имело смысл вкладывать в него денежные средства, и оценить целесообразность вложения денежных средств в объект инвестирования, который в соответствии с бизнес-планом должен принести инвестору через 3 года 1500 тыс. р.
Методические указания: использовать формулы (2.1.7), (7.1.10);
Дано: P =1 млн р. F =1,5 млн р.
n = 3 года _______________
|
Решение: Найдем, сколько, как минимум, должен получить инвестор через 3 года, чтобы реальная доходность была на уровне 5 % в год:
Ожидаемая сумма меньше минимально приемлемой: 1 500 000 р.<1 540 800 р., следовательно, инвестирование нецелесообразно. |
Ответ: Для того, чтобы инвестирование было целесообразно, проект должен принести через три года не менее 1,54 млн. р., поэтому инвестирование нецелесообразно.
Задача 7.1.12.
Рост цен за 3 года составил 7 %. Оценить среднегодовой темп и индекс инфляции.
Методические указания: 1) использовать формулы (2.1.7) и (2.1.9);
2)
ввести обозначения:
![]() -
среднегодовой темп инфляции,
-
среднегодовой темп инфляции,
![]() -
темп инфляции за n лет.
-
темп инфляции за n лет.
Дано:
|
Решение: Среднегодовой темп инфляции рассчитывается, исходя из среднегодового индекса инфляции, который, в свою очередь определяется как:
|
Получаем:
![]()
Отсюда
![]()
Ответ: Среднегодовой темп инфляции 2,28 %, годовой индекс инфляции 1,0228, или 102,28 %.
Задача 7.1.13.
Гражданин заключил договор вклада по 15 % годовых. Прогнозируемый темп инфляции составляет 1 % в месяц. Оценить реальную процентную ставку.
Методические указания: 1) использовать формулы (2.1.7) и (2.1.9);
2) ввести обозначения: - темп инфляции в месяц, - годовой темп инфляции.
Дано:
_________ r = ? |
Решение:
Годовой
темп инфляции рассчитаем на основе
формулы для нахождения эффективной
ставки процента:
|
Реальную доходность (ставку процента) найдем с помощью формулы Фишера:

Ответ: Реальная процентная ставка (доходность) 2,04 % в год.
Задача 7.1.14.
Потребность в оборотных средствах предприятия в отчетном году 1,2 млн долл., прибыль составила 0,5 млн долл. Темп инфляции - 15 %. Всю ли прибыль предприятие может изъять из оборота и пустить на социальные нужды?
Методические указания: 1) использовать формулу (2.1.7);
2) ввести обозначения: - годовой темп инфляции, ОбСо — потребность в оборотный средствах в отчетном году, ОбСп — планируемая потребность в оборотных средствах, По — прибыль в отчетном году, Пс — прибыль на социальные нужды.
Дано: ОбСо=1,2 млн.долл. По = 0,5 млн.долл.
Пс = ? |
Решение: Для поддержания своего функционирования на неизменном уровне в следующем году предприятию надо будет иметь:
ОбСп
= ОбСо Иначе говоря, предприятие должно нарастить оборотные средства на величину: |
ОбС = ОбСп — ОбСо = 1,32 — 1,2 = 0,12 млн долл.
Следовательно, на социальные нужды можно направить:
Пс = По — обС = 0,5 — 0,12 = 0,38 млн долл.
Ответ: На социальные нужды предприятие может направить не более 380 тыс. долл.
Задача 7.1.15.
Оценить влияние инфляции на баланс предприятия за некоторый период [t0, t1]. Построить модели, описывающие финансовое состояние предприятия на конец периода, а также рассчитать полученную им в результате изменения цен прибыль или убыток. В рассматриваемый период хозяйственные операции не совершались. Темп инфляции составил 12 %. Темп изменения текущей оценки немонетарных активов составил 18 % . Баланс предприятия в начальный момент t0 представлен в табл. 7.1.1.
Таблица 7.1.1 — Баланс предприятия в момент t0, млн р.
Актив |
Пассив |
|||
Немонетарные активы Монетарные активы Баланс |
85 12 |
Собственный капитал Монетарные обязательства Баланс |
30 67 |
|
97 |
97 |
|||
Методические указания: 1) изучить п. 7.1.2 контента; 2) принять во внимание, что инфляционная прибыль представляет собой приращение капитала за счет роста цен, а также за счет инфляционного роста превышения монетарных обязательств над монетарными активами; 3) ввести обозначения: НА — немонетарные активы; МА — монетарные активы; СК — собственный капитал; МО — монетарные обязательства; Б0 — валюта баланса (авансированный капитал) в начале периода; Б1 — валюта баланса в конце периода; Пи — прибыль инфляционная.
Дано: НА = 85 млн р. МА = 12 млн р. СК = 30 млн р. МО = 67 млн р. Ti = 0,12 r = 0,18 ________________ Пи = ? |
Решение: В момент времени t0 финансовое состояние предприятия выражается балансовым уравнением: МА + НА = СК + МО. Последовательно рассмотрим несколько ситуаций. Ситуация 1. Учет ведется в неизменных ценах (по себестоимости). Поскольку хозяйственных операций не совершалось, активы и пассивы фирмы не изменятся, а балансовое уравнение на конец периода будет выглядеть следующим образом: |
МА + НА = СК + МО |
12 + 85 = 30 + 67 |
97 = 97 |
Инфляционная прибыль равна нулю (Пи = 0), поскольку влияние инфляции не отражено в учете и отчетности.
Ситуация 2. Учет ведется в денежных единицах одинаковой покупательной способности (методика GPL), с учетом общего индекса цен.
Здесь возможны два варианта рассмотрения. В первом варианте предполагается пересчет немонетарных активов с учетом индекса цен. Балансовое уравнение примет вид:
МА + НА (1 + Ti) = СК + НА Ti + МО |
12 + 85 (1 + 0,12) = 30 + 85 0,12+67 |
107,2 = 107,2 |
Полученное изменение НА Ti=85 0,12=10,2 млн р. может трактоваться как изменение капитала собственников ( СК — дооценка внеоборотных активов) и соответственно как инфляционная прибыль (Пи).
Второй (более строгий и методологически правильный) вариант предполагает учет влияния инфляции путем сопоставления монетарных активов и монетарных обязательств. Такой подход обусловливается тем, что монетарные обязательства в условиях инфляции приносят косвенный доход, а монетарные активы — косвенный убыток. В этом варианте балансовое уравнение будет иметь следующий вид:
МА + НА (l + Ti) = МО + СК (1+ Ti) + Ti (МО — МА) |
12 + 85 1,12 = 67 + 30 1,12 + 0,12 (67 — 12) |
12 + 95,2 = 67 + 33,6 + 6,6 |
107,2 =107,2. |
Вследствие инфляции величина авансированного капитала увеличилась на:
Б = Б1 — Б0 = 107,2 — 97,0 = 10,2 млн р.
Однако не весь рост произошел за счет самовозрастания величины собственного капитала из-за обесценения рубля, а именно:
СК = 33,6 — 30 = 3,6 млн р.
За счет превышения монетарных обязательств над монетарными активами получена инфляционная прибыль:
Пи = Ti (МО — МА) = 0,12 (67 — 12) = 6,6 млн.р.
Ситуация 3. Учет ведется в текущих ценах (методика ССА) с использованием индивидуальных индексов цен.Балансовое уравнение имеет следующий вид:
![]() .
.
В нашем случае, поскольку индивидуальные индексы цен всех немонетарных активов одинаковы, это уравнение примет вид:
12 + 85 1,18 = 30 + 67 + 85 0,18
112,3 = 112,3.
Полученный в результате изменения цен условный доход может трактоваться либо как инфляционная прибыль, либо как инфляционное приращение капитала:
![]()
или
Пи = 112,3 — 97,0 = 15,3 млн р.
Ситуация 4. Учет ведется в текущих ценах и денежных единицах одинаковой покупательной способности (комбинированная методика), балансовое уравнение имеет следующий вид:

В этой модели отражается как влияние инфляции, так и изменение цен на конкретные виды активов, продукции и товаров.
Вследствие инфляции и роста цен на активы данного предприятия величина авансированного капитала увеличилась на:
Б = Б1 — Б0 = 112,3 — 97,0 = 15,3 млн р.
в том числе за счет самовозрастания величины собственного капитала, обеспечивающего сохранение его покупательной способности на:
СК = 30 1,12 — 30 = 3,6 млн р.;
за счет относительного изменения цен на активы предприятия по сравнению с уровнем инфляции — на:
НА = НА (r — Ti) = 85 (0,18 — 0,12) = 5,1 млн р.,
за счет превышения монетарных обязательств над монетарными актива?ми — на:
(МО — МА) = Ti (МО — МА) = 0,12 (67-12) = 6,6 млн р.
Таким образом, общее приращение авансированного капитала составило:
Б = СК + НА + (МО — МА) = 3,6 + 5,1 + 6,6 = 15,3 млн р.
Последние два приращения можно трактовать как инфляционную прибыль и рассчитывать по формуле
Пи = НА + (МО — МА) = 5,1 + 6,6 = 11,7 млн р.
Ответ: 1) в случае ведения учета в неизменных ценах инфляционная прибыль равна нулю; 2) в случае ведения учета в денежных единицах одинаковой покупательной способности с учетом общего индекса цен инфляционная прибыль равна 6,6 млн р. (в качестве инфляционной прибыли может быть рассмотрен весь прирост капитала 10,2 млн р.); 3) в случае ведения учета в текущих ценах с использованием индивидуальных индексов цен инфляционная прибыль равна 15,3 млн р.; 4) в случае ведения учета в текущих ценах и денежных единицах одинаковой покупательной способности инфляционная прибыль равна 11,7 млн р.
Задача 7.1.16.
Прогнозируемое значение среднемесячного темпа роста цен — 3 %. За какой период времени деньги обесценятся: а) в 2 раза, б) в 3 раза?
Методические указания: 1) использовать формулы (7.1.5) и (7.1.6);
2) ввести обозначения: - однодневный темп изменения цен; n — число дн.; k — количество раз, в которое обесцениваются деньги; 3) чтобы некоторая сумма обесценилась в k раз, значение коэффициента падения покупательной способности денежной единицы должно быть равно 1/ k или, что то же самое, индекс цен должен быть равен k.
Дано: |
Решение: |
Найдем однодневный темп инфляции (в месяце 30 дн.).
![]()
Таким образом, однодневный темп инфляции составляет 0,0986 %, т. е. ежедневно цены увеличиваются на 0,0986 %, что приводит к увеличению цен за год на 42,6 %. Из формулы (24.8) следует: чтобы некоторая сумма S обесценилась в k раз, значение коэффициента падения покупательной способности денежной единицы должно быть равно 1/ k или, что то же самое, индекс цен должен быть равен k.
Исходная сумма обесценивается в 2 раза (k = 2):
![]() .
Отсюда искомое число дн. n
= 703 дн.
.
Отсюда искомое число дн. n
= 703 дн.
Исходная сумма обесценивается в 3 раза (k = 3):
![]() .
Отсюда искомое число дн. n
=1115 дн.
.
Отсюда искомое число дн. n
=1115 дн.
Ответ: При среднемесячном темпе инфляции 3 % любая исходная сумма, находящаяся без движения, например, омертвленная в виде денег как запас средств, обесценится вдвое через 703 дн., т. е. примерно через 1,9 года, а в 3 раза — через 1115 дн., т. е. через 3 года.








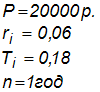

 ,
а годовой индекс, в свою очередь,
равен:
,
а годовой индекс, в свою очередь,
равен:








