Глава 2. Термодинамика химических реакций

2.1. Примеры решения задач

Пример 1. Определить стандартную теплоту реакции дегидрирования этана до метана, ацетилена и H₂ в газовой фазе при стандартных условиях и при том же давлении и температуре 125 ^ОС (398 К);

1) Исходя из теплот сгорания веществ участвующих в реакции;

2) Исходя из теплот их образования.

Вещество	C2H6, ккал/моль	CH4, ккал/моль	C2H2, ккал/моль	H2, ккал/моль
Δ	372,82	212,8	310,62	68,310
Δ	-20,236	-17,889	54,194	-

Решение.

Δ = .

Δ = .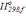

2C₂H₆→2CH₄+C₂H₂+H₂

Δ .

Δ 54,194+(−17,889∙2)−(−2∙20,236) = 58,89.

Δ Δ + .

	C2H6	CH4	C2H2	H2
a	1,074	4,171	5,607	6,95
b∙103	43,561	14,45	20,499	-0,20
c∙106	-17,891	0,267	-13,944	0,48

Δ = 58,89 ккал/моль = 58,89∙10³ кал/моль.

Δ = а+bT+cT².

Допустим, что 1 Дж = 1 кал.

Δ = 58,89∙10³+ 18,751−37,923∙10^-3∙398+22,852∙10^-6∙398²)dT =

58,89∙10³ +18,751(398−298)−37,923∙10^-3∙ +22,852∙10^-6∙ = 60,962 ккал/моль.

Δа = = (2∙4,171+5,607+6,95)−(2∙1,074) = 18,751,

Δb = = (2∙1445+20,499−0,20)−(2∙43,561) = −37,923∙10^-3,

Δс = = (0,267∙2−13,944+0,48)−(−17,891)∙2 = 22,852∙10^-6.

Пример 2. Вычислить теплоемкость CH₄ при 25 ^ОС, если при той же температуре и давлений 1 атм = 8,536 кал/К∙моль, считать что:

1) CH₄− идеальный газ;

2) CH₄− реальный газ.

Решение.

Формула Майера:

.

где 8,31 = 1,987 кал/К∙моль.

1 кал = 4,1868 Дж; 1 Дж = 0,2388 кал.

Формула для нахождения теплоемкости идеального газа:

R = 8,536−1,987 = 6,549 кал/К∙моль.

где R работа расширения системы при изменении Т на 1 ^ОС производимой в результате подвода дополнительного тепла.

Формула для нахождения теплоемкости реального газа:

.

где a = 0,00449 см⁶∙атм/моль; 1 см⁶∙1 атм = 0,0242 кал; 2а = 0,000217.

= 6,5489 кал/К∙моль.

CH_4, при этих условиях в состоянии реального газа ведет себя как идеальный газ.

Пример 3. Для газообразного 1,3-бутадиена теплоемкость в интервале температур от 298 до 1500 К задано уравнение:

0,707+81,282∙10⁻³T−53,463∙10^-6T² кал/К∙моль.

Определить среднюю теплоемкость в интервале температур от 400 до 500 К.

Решение.

Для решения используем формулу:

,

когда нагревание либо охлаждение системы не сопровождается фазовыми переходами.

.

= ∙(0,707∙100+81,282∙10^-3∙ −53,463∙10^-6∙ ) = 4,5928 кал/К∙моль.

Пример 4. Возможна ли реакция дегидроциклизации нормального октана в параксилол при 800 К, если известны следующие термодинамические параметры:

соед-е пар-р	C8H18	параксилол	H2	Δ
Δ ,	-49,82	4,290	0	5 4,11
Δ ,	111,55	84,23	31,211	97,524
a	1,651	-6,196	6,95	19,953
b∙103	177,317	145,716	-0,2	-32,401
c∙106	-94,95	-83,786	0,48	13,084

вычисленные

значения

При Т = 800 К известны: М_о=0,9537, М₁∙10^-3=0,1574, М₂∙10^-6=0,0733. Найти Δ .

Решение.

Δа = =(−6,196+6,95∙4)−1,651 = 19,953;

Δb = = 145,716+(4∙(−0,2)) −177,317 = −32,401∙10⁻³;

Δс = = −83,786+4∙0,48−(−94,95) = 13,084∙10⁻⁶.

Δ = 4,290+49,82 = 54,110.

Δ = 4∙31,211+84,23−111,55 = 97,524 кал/моль∙К.

= −97,524−19,953∙0,9537−(−32,401∙10⁻³) ∙0,1574∙10³ −13,084∙10⁻⁶ ∙ 0,0733∙10⁶ = −26,33ккал/моль;

= = −26,33ккал/моль.

Пример 5. Пользуясь справочными данными найти зависимость мольной теплоты испарения жидкого этанола от температуры в интервале от 283 до 348 К при P=1 атм. В качестве нижнего предела интегрирования принять 0 К.

	С2H6(жид)	С2H6(газ)
Δ , ккал/моль	−66,356	66,356
a	25,46	4,946
b∙103	−39,6	49,087
c∙106	137	−-23,885

Решение.

С₂H_6(жид) → С₂H_6(газ)

Δ = = −56,240−(−66,356) = 10,116,

Δа = = 4,946−25,46 = −20,514,

Δb = = 49,087∙10⁻³−(−39,6∙10⁻3) = 88,687∙10⁻³,

Δс = = −23,885−137 = −160,885∙10⁻⁶.

= −20,514∙298+ ∙88,687∙10⁻³+ ∙(−160,885∙10⁻⁶) = −3594,49.

10,116∙10³=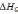 −3594,49

где =13,710 ккал/моль.

= + ΔаT+ T²+ T³.

= 13,710+(−20,514T)+44,343∙10⁻³T²−53,628∙T³∙10⁻⁶.

Пример 6. Стандартная теплота реакции:

CH₄+CO₂→CO+H₂,

который протекает в газовой фазе при 900 К равна 260119 Дж. Даны теплоемкости реагентов при различных реагентах.

Т ср	800	1000
CH4	63,18	72,0
CO2	40,21	42,77
CO	29,81	30,36
H2	28,96	29,15

Найти Δ . Принять что в интервале от 800 до 1000 средняя теплоемкость:

Результаты расчета сравнить с литературной величиной, которая равна 259491 Дж.

Решение.

CH₄+CO₂→2CO+2H₂

Δ = .

Δ = .

Δ = 2∙29,81+28,96∙2−69,18−40,21 = 14,15,

Δ = 2∙30,36+2∙29,15−72,0−42,7 = 4,25,

Δ = 0,5(14,15+4,25)=9,2.

= +( (900-800)).

= +( (900-800)).

= ( + ) = (14,15+9,2) = 11,675.

= −11,675∙100 = 260119−11,675∙100 = 258951,5 Дж.

отличается от табличного значения на 0,5 кДж.

Пример 7. Средняя мольная теплоемкость CH₄ при постоянном объеме в интервале температур от 298−1500 К дана выражением:

_υ = 8,983+30,229∙10⁻³T+3,722∙10⁻⁷T² Дж/ К∙моль,

найти истинную мольную теплоемкость при постоянном давлении и температуре 25 ^OC считать, что CH₄ подчиняется законам идеального газа. Использовать выражения:

Δ = .

Решение.

8,31 = 1,987 кал/К∙моль.

_υ = 8,983+30,229∙10⁻³T+3,722∙10⁻⁷T² Дж/ К∙моль,

_υ = 8,983+30,229∙10⁻³(1500−298)+3,722∙10⁻⁷(1500−298)²,

= 8,983+8,31+30,229∙10⁻³T+3,722∙10⁻⁷T²,

= 17,293+30,229∙10⁻³T+3,722∙10⁻⁷T²,

= 17,293T+30,229∙10⁻³T²+3,722∙10⁻⁷T³.

= 17,293+60,458∙10⁻³T+11,166∙10⁻⁷T² = ,

= 17,293+60,458∙10⁻³∙298+11,166∙10⁻⁷ ∙298² = 35,409 Дж/ К∙моль.

Пример 8. Для реакции:

CO_(г)+H₂O_(г)→CO_2(г)+H_2(г)

рассчитать энтальпию реации через величины энтальпии разрывающихся и образующихся связей при 298 К и 1 атм. Считать, что ,

Известно, что =

Р ешение. :С=О + О → С=О +H−H

H H O

^{разр образ образ}

ΔH_p = .

ΔH_p = 2∙ + _образ = 2∙463+(−532−436) = −42 .

Пример 9. Рассчитать среднюю H диссоциации химической связи в молекуле метана по уравнению

CH_4(г)→С_(г) + 4H_(г)

−74,85 718,38 217,94

Решение. Используем справочные данные :

= 718,38+4∙217,94−(−74,85) = 1664,99 .

Теплота пошедшая на разрыв четырех связей:

/4 = 416,25 .

Пример 10. Зависимость К_р от температуры для реакции:

CO_(г)+H₂O_(г)→CO_2(г)+H_2(г)

Определяется следующим уравнением:

Найти стандартную теплоту реакции при 25 ^OC, используя:

1) Закон Гесса;

2) уравнение изобары .

Решение.

соед-е пар-р	CO, ккал/моль	H2, ккал/моль	CO2, ккал/моль	H2Oг, ккал/моль
	−26416	0	−94052	−57798

Δ = = 0+(−94052)−(−26416)−(−57798) = −9,838 ккал/моль

= 2,303

= ∙2,303−0,783 +0,00099029Т,

= −0,783 +0,00099029Т,

−0,783 +0,00099029,

−9,972 ккал/моль.

Пример 11. Определить стандартную теплоту реакции:

CO+2H₂↔CH₃OH

если известно, что на других реакциях:

1) 2H₂+HCOOCH₃↔2CH₃OH

2) CH₃OH+CO↔HCOOH

Найдено экспериментальное выражение констант равновесия:

Решение.

= .

=2,303 .

= .

= ∙RT ²= 22,807 ккал/моль.

.

Пример 12. Вычислить состав равновесной смеси реакции превращения из пентена в децен, протекающий в газовой фазе, если в начале реакции мольное соотношение децена и пентена=1:1, =2,617 атм^-1. Считать, что пентен и децен подчиняются законам идеальных газов, Т процесса 400 К. Найти мольные доли каждого компонента.

Решение.

2С₂H₅↔C₁₀H₁₀

2A↔B

	С2H5	С10H10
τ=0	1	1
τ=τp	1−2x	1+x
и зрасход образовано	2x	x
υi	2	1
∑ni	2−x

∑n_i=1−2x+1+x=2−x.

N_A = ,

N_B= ,

где =2,617 атм^-1,

K_P = = 13,69 атм^-1.

K_P = .

Р_i=N_i∙Р_общ.

P_A= ,

P_B= ,

K_P = = ,

K_P = 13,69 атм^-1.

13,69 = ( ) = ,

13,69−54,76x+54,76 −2−x− = 0,

55,76 −55,76 +11,69 = 0,

D = 501,84,

x₁ = =0,7,

x₂ = =0,3.

x₁ и x₂ проверяем подстановкой в N_A и N_B, x₁ не подходит, так как N_A становится отрицательным.

N_A = = 0,235∙100% = 23,5%,

N_B = 0,765∙100% = 76,5%.

∑N = 1.

A=23,5%,

B=76,5%.

Пример 13. Рассчитать состав газообразной равновесной смеси в реакции дегидроциклизации n-октана в параксилол при 500 К и 1 атм, если −2,077. Состав выразить в массовых процентах.

Решение.

А↔В+4С

	С8H18	С8H10	H2
τ=0	1	0	0
τ=τp	1−x	x	4x
и зрасход образовано	x	x	4x
υi	−1	1	4
∑ni	4x+1

N_i = ,

N_A = ,

N_B = ,

N_C = .

P_A= N_A∙P_общ = ,

P_B = ,

P_C = .

K_P = = ,

K_P = 0,0084.

0,0084 = .

P⁴=1

,

K_P = M∙ ,

,

,

.

При x=0,194:

N_A = = 0,454,

N_B = = 0,109,

N_C = = 0,437.

∑N_i=1.

A=45,4%.

N_A = .

m_A = = 0,454∙114 = 51,756,

m_B = 0,11∙106 = 11,66,

m_C = 0,437∙2 = 0,874,

∑m_i = 64,29.

G_A = = 0,805∙100% = 80,5%,

G_B = = 18,14%,

G_C = = 1,36%,

∑G_i = 100%.

Пример 13. Рассчитать состав равновесной смеси изомеризации этилбензола при 600 К и 1 атм в газовой фазе, если известно что

	ЭБ	О-ксилол	М-ксилол	П-ксилол
ΔG600, ккал/моль	57,646	56,103	55,099	56,060

Решение.

3 обратимые реакции:

ΔG_P600 = .

1) ΔG_P1,600 = 56,060−57,646 = −1,586;

2) ΔG_P2,600 = 55,099−57,646 = −2,547;

3) ΔG_P3,600 = 56,103−57,646 = −1,543.

ΔG = −RT .

где R = 1,987 кал/К∙моль, тогда

= 3,78,

= 8,45,

=3,648.

	П−кс	М−кс	О−кс	ЭБ
τ=0	0	0	0	1
τ=τp	x1	x2	x3	1−(x1+ x2+ x3)
и зрасход образовано	x1	x2	x3	x1+ x2+ x3
υi	1	1	1	−1
∑ni	1

∑n_i = x₁+ x₂+ x₃+1−(x₁+ x₂+ x₃) = 1.

N_i =

N₁ = ,

N₂ = x₂,

N₃ = x₃,

N_ЭБ =1−(x₁+ x₂+ x₃).

P_i = N_i∙P_общ,

где P_общ=1, P_i = N_i.

K_P = ,

= = 3,78 решаем систему уравнений.

= = 8,45

= = 3,648

1) 3,78 x₁ = 1−x₁ −x₂− x₃;

2) 8,45 x₂ = 1−x₁ −x₂− x₃;

3) 3,648 x₃ = 1−x₁ −x₂− x₃;

= 15,878,

,

,

,

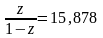z = 15,878 (1−z),

z = 15,878−15,878z,

16,878z = 15,878,

z = 0,94.

,

x₁ = 0,224.

,

x₂ = 0,5.

,

x₃ = 0,218.

Пример 14. Вычислить летучесть водорода при 500 К и давлении 250 атм, если известно, что Т_кр = 33,3 К; Р_кр = 12,8 атм; Z_кр = 0,29.

Решение.

.

.

где 1,1.

.

Пример 15. Рассчитать константы равновесия: К_γ, К_р, если Т = 800 К, Р = 2 МПа. Для реакции разложения нормального пентана до этилена и пропана

C₅H_12(Г)↔ C₂H_4(Г) + C₃H_8(Г)

Если известно, что ∆G₈₀₀ = −16,050 кДж/моль.

соединение параметр	А	В	С
Ткр (К)	469,8	370	282,4
Ркр (МПа)	3,37	4,26	5,04

Решение.

.

.

,

,

.

, ; .

; ; .

.

.

,

,

.

Пример 16. Рассчитать состав равновесной смеси, получающаяся при полимеризации пропилена в газовой фазе: