14. Простейшие связи между прямой и двойственной задачами
Между
прямой и двойственной задачами можно
установить следующую взаимосвязь:
1. Если прямая задача на максимум, то
двойственная к ней — на минимум, и
наоборот.
2.
Коэффициенты 
при
переменных в целевой функции двойственной
задачи являются свободные члены в
системе ограничений исходной задачи.
3. Свободные члены 
ограничений
(правые части) двойственной задачи
являются коэффициентами при переменных
в целевой функции исходной задачи.
4. Матрицы ограничений прямой и
двойственной задач являются
транспонированными друг к другу.
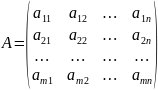матрица
коэффициентов в исходной задаче
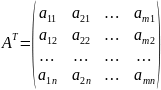матрица
коэффициентов в двойственной задаче
5. Если прямая задача на максимум, то ее
система ограничений представляется в
виде неравенств типа 
.
Двойственная задача решается на минимум,
и ее система ограничений имеет вид
неравенств типа 
.
6. Каждому ограничению одной задачи
соответствует переменная другой задачи:
№ переменной совпадает с № ограничения.
То есть число ограничений прямой задачи
равно числу переменных двойственной,
а число ограничений двойственной —
числу переменных прямой.
Если ограничение исходной задачи является равенством, то соответствующая переменная двойственной задачи может принимать как положительные, так и отрицательные значения
Математические модели пары двойственных задач могут быть симметричными и несимметричными.
15. Теоремы двойственности.
Теоремы двойственности позволяют установить взаимосвязь между оптимальными решениями пары двойственных задач: можно либо найти оптимальное решение другой задачи, не решая ее, либо установить его отсутствие. Возможны следующие случаи: обе задачи из пары двойственных имеют оптимальные решения; одна из задач не имеет решения ввиду неограниченности целевой функции, а другая – ввиду несовместности системы ограничений.
Первая теорема двойственности.
Для
двойственных задач линейного
программирования имеет место один из
взаимоисключающих случаев: В прямой и
двойственной задачах имеются оптимальные
решения, при этом значения целевых
функций на оптимальных решениях
совпадают: 
;
В прямой задаче допустимое множество
не пусто, а целевая функция на этом
множестве не ограничена сверху. При
этом у двойственной задачи будет пустое
допустимое множество. В двойственной
задаче допустимое множество не пусто,
а целевая функция на этом множестве не
ограничена снизу. При этом у прямой
задачи допустимое множество оказывается
пустым; Обе из рассматриваемых задач
имеют пустые допустимые множества.
Вторая теорема двойственности (теорема о дополняющей нежесткости):
Пусть 
–
допустимое решение прямой задачи, а 
–
допустимое решение двойственной задачи.
Для того, чтобы они были оптимальными
решениями соответствующих взаимодвойственных
задач, необходимо и достаточно, чтобы
выполнялись следующие соотношения:
Эти условия устанавливают связь между оптимальными значениями прямой и двойственной задач и позволяют, зная решение одной из них, находить решение другой задачи.
Третья теорема. Теорема об оценках:
Значения
переменных 
в
оптимальном решении двойственной
задачи представляют собой оценки
влияния свободных членов 
системы
ограничений – неравенств прямой задачи
на величину 
:
.
Диапазон
изменения компонент вектора 
,
в котором сохраняется оптимальный
базис, называется областью устойчивости
оптимальных оценок.