6.Различные формы записи задачи линейного программирования и их эквивалентность

Общая задача линейного программирования :

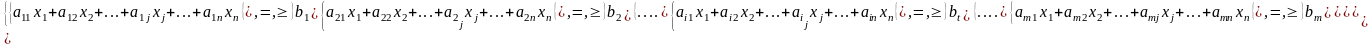
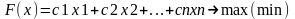
aij,bij,Cj- заданные постоянные величины

2 формы записи:

1)стандартная : ≤ b_m, F(x)→max

2)каноническая: = b_m, F(x)→max

Правила приведения задач линейного программирования к стандартной и канонической формам:

1.Превращение max в min и наоборот (умножением на (-1) )

2.Смена знака неравенства (умножением на (-1)) из ≥ в ≤ и наоборот

3.Превращение равенства в систему нер-в

a_i1+a_i2x₂+…+a_inx_n=b_i

заменить системой 2-х нер-в

a_i1x₁+a_i2x₂+…+a_inx_n≤b_i

a_i1x₁+a_i2x₂+…+a_inx_n≤b_i

Для приведения станд-й задачи к канонической форме должны быть введены дополнит-е переменные

Если ≥, то вычит-ся переменные.

7. Понятие выпуклого множества. Теорема о выпуклости множества допустимых решений задачи линейного программирования

Множество (область)   называется выпуклым, если оно, вместе с любыми двумя своими точками, содержит в себе отрезок, соединяющий эти точки.(круг, область, сектор, отрезок)

Рассмотрим n - мерное евклидово пространство    и пусть   - точка в этом пространстве.

Рассмотрим две точки   и  , принадлежащие  Множество точек  , которые могут быть представлены в виде

(в координатах это записывается так: ,

называется выпуклой комбинацией точек   и

, или

отрезком, соединяющим точки   и  . Сами точки   и   называются концами отрезка. В случаях n =2 и n =3 это - отрезок в обычном понимании этого слова на плоскости или в пространстве. Заметим, что при l =0  , а при l =1  , т.е. при l =0 и l =1 получаются концы отрезка.

 

Пусть в

заданы k точек

. Точка

 , где все  и   называется выпуклой комбинацией точек  .

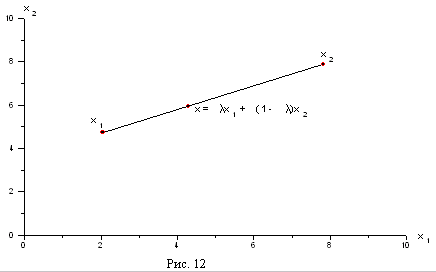
Пусть   есть некоторая область в пространстве   (другими словами,

G есть некоторое множество точек из

).

 

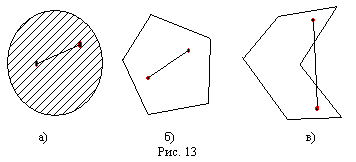
На этих рисунках "а" и "б" - выпуклые множества, а "в" не является выпуклым множеством, так как в нём есть такая пара точек, что соединяющий их отрезок не весь принадлежит этому множеству.

Теорема.Допустимая область задачи линейного программирования является выпуклым множеством.

Доказательство.

1. В стандартной форме в матричных обозначениях допустимая область G определяется условием

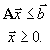
Пусть

и

принадлежат G , т.е.

Но тогда для

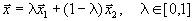
имеем

т.е. x принадлежит G и, следовательно, выпукло.

 

2. В канонической форме область G определена условиями

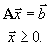
Пусть   и   принадлежат G, т.е.

 .

Но тогда для

имеем

т.е. и, следовательно, G выпукло. Теорема доказана.

Таким образом, допустимая область в задаче линейного программирования является выпуклым множеством. По аналогии с двумерным или трехмерным случаями, при любом n эту область называют выпуклыммногогранником в n - мерном пространстве 

многогранником в n - мерном пространстве  8. Понятие выпуклого многогранника. Теорема о связи крайних точек выпуклого многогранника с оптимальными решениями задачи линейного программирования.

Выпуклый многогранник (многоугольник) – это выпуклое замкнутое множество точек пространства (плоскости), имеющее конечное число угловых точек, если оно ограниченное. Оптимальное решение задачи линейного программирования находится в одной из вершин выпуклого многогранника. Это вытекает также из ограничений в задаче линейного программирования. Если существуют n действительных неотрицательных переменных проектирования z, которые поэтому являются базисными, то остальные переменные являются внебазисными. Это значит, что k1 из т ограничений должны удовлетворяться в виде равенств. 

Предположим, что на некоторой интеграции текущее оптимальное решение задачи линейного программирования получено с помощью симплексного алгоритма. 

Наименьшего значения линейная форма достигнет тогда, когда прямая будет проходить через крайнюю точку области допустимых решений, наиболее удаленную от начала координат. Координаты этой точки определяют оптимальное решение задачи линейного программирования. Нам остается только определить все вершины, вычислить в каждой из них целевую функцию и выбрать ту, которая оптимизирует данную функцию.

Раз экстремум целевой функции достигается на одной из вершин многогранника допустимой области, то нет необходимости исследовать все точки области. Надо лишь "пройтись" по вершинам многогранника. Но для этого нужно уметь переходить от одной вершины к другой.

Пусть нам известен какой-то опорный план (вершина), соответствующий m векторам из первоначальной системы n векторов. Будем считать, что

этими векторами являются первые m векторов

из системы

векторов  .

Опорный план имеет вид

,

где все  .

Для него

.

Так как векторы   линейно независимы, то они образуют базис

в m -мерном пространстве и любой из векторов

может быть разложен

по этому базису, то есть для любого

верно разложение

,

где   - коэффициенты разложения по базису (координаты вектора   в базисе   .

Возьмем какой-то вектор, не входящий в наш базис, скажем, вектор  . Для него

.

Пусть хотя бы один из коэффициентов  положителен. Возьмем некоторую величину  , умножим на неё обе части равенства и вычтем из . Тогда получим

Вектор

в случае неотрицательности всех своих компонент является планом. Те компоненты, где   , будут автоматически неотрицательны. Чтобы остальные компоненты были неотрицательны, надо, чтобы

Отсюда имеем:

Возьмем

,

где минимум берется по всем тем индексам i , для которых  . Очевидно, что если  , то все компоненты плана   будут неотрицательны.

Но давайте возьмем q в точности равным  .

Пусть, например,

достигается при i =1, то есть  .

Но тогда

компонента

обратится в ноль и мы получим план

,

где

который опять содержит ровно m отличных от нуля положительных компонент.

Докажем, что  новая вершина есть новый опорный план. Действительно, этому новому плану соответствуют векторы  . Допустим, что они линейно зависимы, то есть существуют такие числа  , не все равные нулю, что векторы

уже были линейно независимы, поэтому  . Но тогда  ,где .

.

Так как разложение по базису определяется однозначно, то должно быть , в частности, должно быть  =0. Это противоречит тому, что  >0. Значит, система векторов   линейно независима и мы перешли к новой вершине, то есть получили новый опорный план.

Отметим следующее. Если все  , то мы не в состоянии проделать эту процедуру. Зато, неограниченно увеличивая , мы можем получить план со сколь угодно большими компонентами. Значит, в этом случае допустимая область неограничена.