24. Игры с «природой». Основные понятия и критерии максимакса, Вальда, Сэвиджа и Гурвица.

Отличительная особенность игры с природой состоит в том, что в ней сознательной действует только один из участников (игрок 1). Игрок 2 (природа) сознательно не действует, а выступает как неимеющий конкретные цели партнер по игре, т е выбирает очередные ходы случайным образом. Термин «природа» характеризует некую объективную действительность, которую не следует понимать буквально.

При решении игр с природой сначала составляется матрица выигрышей и определяется 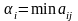- минимальный выигрыш и 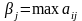- максимальный проигрыш. Далее определяется максимальная стратегия игрока 1. А затем составляется матрица рисков. Элементами матрицы рисков являются r_ij – риск.

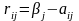
При принятии решений в условиях полной неопределенности наилучшее решение выбирается по следующим критериям: критерий максимакса, критерий Вальда, критерий Севиджа, критерий Гурвица.

Критерий максимакса – критерий крайнего оптимизма. Наилучшим признается решение, при котором достигается макс-й выигрыш, равный M=maxa_ij. Этот критерий используется, когда игроки поставлены в безвыходное положение и руководствуются принципом «или пан, или пропал».

Критерий Вальда (максимальный критерий Вальда) – здесь природа рассматривается как агрессивно настроенный и сознательно действующий противник. W=maxmina_ij. В соответствии с этим критерием, из всех самых неудачных результатов выбирается лучший. Это критерий крайнего пессимизма, при котором выбирается перестраховочная позиция игрока, рассчитывающий на худший случай.такая стратегия применяется, когда игрок не столько заинтересован в крупной удаче, сколько хочет застраховать себя от неожиданных проигрышей.

Критерий Севиджа – выбор стратегии аналогичен выбору стратегии по принципу Вальда с тем отличием, что игрок руководствуется не матрицей выигрышей, а матрицей рисков. S=minmaxr_ij.

Критерий Гурвица (критерий пессимизма-оптимизма) – здесь выбор решения основывается на некотором среднем результате, характеризующим состояние между крайним пессимизмом и крайним оптимизмом.

Применительно для матрицы выигрышей: 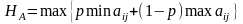, где p – коэф-т пессимизма, его значения находятся в пределах от 0 до +1.

При p=0 – критерий Гурвица совпадает с критерием максимакса. При p=1 - совпадает с критерием Вальда.

Применительно для матрицы рисков:

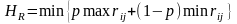
Анализируя в комплексе все критерии, определяется оптимальная стратегия игрока 1.

25. Позиционные игры. Дерево решений.

Позиционные игры – игры, в которых принятие игроками решений (т. е. выбор ими стратегий) рассматривается как многошаговый или даже непрерывный процесс. Другими словами, в позиц игре в ходе процесса принятия решений субъект проходит последовательность состояний, в каждом из которых ему приходится принимать некоторое частичное решение.

Позиционные игры должны включать следующие элементы описания:

1. последовательность личных и случайных ходов игроков;

2. выборы, которые могут делать игроки при каждом личном ходе;

3. исходы случайных ходов и распределение вероятностей этих исходов;

4. информацию, доступную игрокам при выполнении личного или случайного хода;

5. правила окончания игры и подсчеты выигрыша игроков.

Число ходов в данной игре не фиксируется. В общем случае, оно зависит от последовательности выборов, исходов. Однако, правила должны гарантировать, что игра в конце концов закончится.

Позиционные игры удобно задавать графически в виде дерева игры. Дерево состоит из вершин, соединенных между собой ветвями. Вершины дерева называют еще позициями игры, а его ветви - ходами игрока.

Дерево решений – графическое изображение последовательности решений и состояние среды с указанием соответствующих вероятностей и выигрышей для любых комбинаций альтернатив.

Процесс принятия решений с помощью дерева решений в общем случае предполагает выполнение следующих пяти этапов:

1. Формулирование задачи.

2. Построение дерева решений.

3. Оценка вероятностей состояний среды, т.е. сопо­ставление шансов возникновения каждого конкретного события.

4. Установление выигрышей (или проигрышей) для каждой возможной комбина­ции альтернатив (действий) и состояний среды.

5. Решение задачи.

Процедура принятия решения заключается в вычислении для каждой вершины дерева (при движении справа налево) ожидае­мых денежных оценок, отбрасывании неперспективных ветвей и выборе ветвей, которым соответствует максимальное значение ОДО. ОДО рассчитывается как сумма произведений размеров выигрышей на вероятности этих выигрышей.