20. Метод потенциалов решения транспортной задачи. Вырожденная транспортная задача.

Наиболее применяемым методом является – метод потенциалов, при котором каждой i-й строне (j-му поставщику) устанавливается потенциал 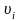, которое можно интерпретировать как цену продукта в пункте поставщика, а каждому j-му столбцу(j-му потребителю) устанавливается потенциал Ui, которое можно применить условно за цену продукта в пункте потребителя.

Данный метод используется для проверки найденного решения на оптимальность.

Критерием оптимальности являются – оценки для свободных клеток и решение считается оптимальным если оценки 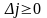(не положительные)

Оценки находятся по формуле:

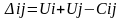
Для заполненных клеток составляются уравнения потенциалов, по следующей зависимости:

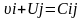
Клетки таблицы, в которые записаны отличные от нуля перевозки, называются базисными, а остальные (пустые) - свободными.

• План называется вырожденным, если количество базисных клеток в

нем меньше, чем m + n −1.

Если на каком-то этапе решения получился вырожденный план, то его необходимо пополнить, проставив в недостающем числе клеток нулевую перевозку и превратив, тем самым, эти клетки в базисные. Общий баланс и суммарная стоимость перевозок плана при этом не изменятся. Однако проводить пополнение плана, выбирая клетки произвольно, нельзя. Приведем условия, которым должен соответствовать пополненный план.

• Циклом в транспортной таблице называется несколько клеток, соединенных замкнутой ломаной линией так, чтобы две соседние вершины ломаной были расположены либо в одной строке, либо в одном столбце. Ломаная линия может иметь точки самопересечения, но не в клетках цикла.

• План называется ациклическим, если его базисные клетки не содержат циклов.

Доказано, что оптимальные планы являются ациклическими, поэтому и первоначальный план также должен удовлетворять этому требованию.

Однако если план оказался вырожденным, то при его пополнении требование ацикличности необходимо учитывать.

21.Основные понятия и определения теории игр. Классификация игр.

Теория игр служит для моделирования оценки воздействия принятого решения на конкурентов.

Игрой называется идеализированная математическая модель конфликтной

ситуации. Стороны, участвующие в конфликте называются игроками, а исход конфликта –выигрышем. Регулярное действие, выполняемое игроком, называется ходом.

Совокупность ходов игрока, совершаемых им для достижения цели игры, называется стратегией. Все возможные действия игроков подчиняются определённым правилам.

Классификацию игр можно проводить: по количеству игроков, количеству

стратегий, характеру взаимодействия игроков, характеру выигрыша, количеству ходов, состоянию информации и т.д.

В зависимости от количества игроков различают игры двух и n игроков. Наиболее изучены игры с двумя игроками. Такие игры называются парными.

По количеству стратегий игры делятся на конечные и бесконечные. Если в игре все игроки имеют конечное число возможных стратегий, то она называется конечной.

Если же хотя бы один из игроков имеет бесконечное количество возможных стратегий, игра называется бесконечной.

По характеру взаимодействия игры делятся на коалиционные и бескоалиционные.

Бескоалиционные – игроки не имеют права вступать в соглашения, образовывать коалиции; коалиционные (кооперативные) – могут вступать в коалиции. В кооперативных играх коалиции заранее определены.

По характеру выигрышей игры делятся на: игры с нулевой суммой (общий капитал всех игроков не меняется, а перераспределяется между игроками; сумма выигрышей всех игроков равна нулю) и игры с ненулевой суммой.

По виду функций выигрыша игры делятся на: матричные, биматричные,

непрерывные, выпуклые и др.

Матричная игра – это конечная игра двух игроков с нулевой суммой, в которой задаётся выигрыш игрока 1 в виде матрицы (строка матрицы соответствует номеру применяемой стратегии игрока 1, столбец – номеру применяемой стратегии игрока 2; на пересечении строки и столбца матрицы находится выигрыш игрока 1, соответствующий применяемым

стратегиям).

Биматричная игра – это конечная игра двух игроков с ненулевой суммой, в которой выигрыши каждого игрока задаются матрицами отдельно для соответствующего игрока (в каждой матрице строка соответствует стратегии игрока 1, столбец – стратегии игрока 2, на пересечении строки и столбца в первой матрице находится выигрыш игрока 1, во второй матрице – выигрыш игрока 2.)

Непрерывной считается игра, в которой функция выигрышей каждого игрока является непрерывной.

Если функция выигрышей является выпуклой, то такая игра называется выпуклой.

Для них разработаны приемлемые методы решения, состоящие в отыскании чистой оптимальной стратегии (определённого числа) для одного игрока и вероятностей применения чистых оптимальных стратегий другого игрока. Такая задача решается сравнительно легко.