19.Методы нахождения начального допустимого базисного решения транспортной задачи: метод «северо-западного угла», метод минимального элемента, метод Фогеля.

Метод «северо-западного угла»

Суть метода:Метод состоит в последовательном переборе строк и столбцов транспортной таблицы, начиная с левого столбца и верхней строки, и выписывании максимально возможных отгрузок в соответствующие ячейки таблицы так, чтобы не были превышены заявленные в задаче возможности поставщика или потребности потребителя.

Шаг 1. Составляют транспортную таблицу.

Шаг 2. Транспортную таблицу начинают заполнять с левого верхнего (северо-западного) угла. При заполнении двигаются по строке вправо и по столбцу вниз. В клетку, находящуюся на пересечении первой строки и первого столбца, помещается максимально возможное число единиц продукции, разрешенное ограничениями на предложение и спрос:  Если а₁ < b₂, то х₁₁ = a₁ и предложение первого поставщика полностью исчерпано. Первая строка вычеркивается, и двигаются по столбцу вниз. В клетку, находящуюся на пересечении первого столбца и второй строки, помещается максимально возможное число единиц продукции, разрешенное ограничениями на предложение и спрос: х₂₁ = = min(a₂,b₁-a₁). Если b₁-a₁ <a₂ то х₂₁ = b₁-a₁. Спрос первого потребителя удовлетворен. Первый столбец вычеркивают и двигаются по второй строке вправо. Заполнив клетку, стоящую на пересечении второй строки и второго столбца, переходят к заполнению следующей третьей клетки второй строки, либо второго столбца. Процесс продолжают до тех пор, пока не исчерпается предложение и не удовлетворится спрос. Последняя заполненная клетка находится в последнем n-м столбце и последней m-й строке.

Поставщики	Потребители				Мощности поставщиков
	В1	В2	В3	В4
А1	4 4	5 2	3	7	6
А2	8	7 4	5 4	4	8
А3	9	3	4 4	5 6	10
Спрос потребит-й	4	6	8	6

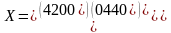- начальный опорный план перевоза груза

F(x)=4*4+5*2+7*4+5*4+4*4+5*6=120д.ед

Метод наименьших стоимостей:

алгоритм получения допустимого начального решения транспортной задачи. В отличие от более простого метода северо-западного угла, в этом методе расчетчик записывает отгрузки, в первую очередь, в те ячейки, где тариф на перевозку груза минимален. Этот метод позволяет получить более приближенное к оптимальному решение, которое, однако, может потребовать дальнейшей оптимизации методом потенциалов.

Шаг 1. Составляют транспортную таблицу.

Шаг 2. Выбирают клетку таблицы, которой соответствует минимальное значение тарифа, и переходят на шаг 3.

Шаг 3. В выбранную клетку аналогично методу "северо-западного" угла помещают максимально возможное число единиц продукции, разрешенное ограничениями на предложение и спрос. После этого, если предложение производителя исчерпано, вычеркивают соответствующую строку; если спрос удовлетворен, вычеркивают соответствующий столбец.

Если все клетки заполнены или вычеркнуты, то план перевозок построен. В противном случае переходят к шагу 2 без учета заполненных и вычеркнутых клеток.

Поставщики	Потребители				Мощности поставщиков
	В1	В2	В3	В4
А1	4	5	3 6	7	6
А2	8 2	7	5	4 6	8
А3	9 2	3 6	4 2	5	10
Спрос потребит-й	4	6	8	6

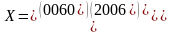
F(x)= 3*6+2*8+4*6+9*2+3*6+4*2=102д.ед.

Метод Фогеля:

Шаг 1. Составляют транспортную таблицу. 

Шаг 3. Для каждой строки и каждого столбца транспортной

таблицы определяют разность между наименьшим тарифом и ближайшим к нему значением. Переход к шагу 3.

Шаг 3. В строке или в столбце, которым соответствует наибольшая разность, выбирают клетку с наименьшим тарифом. Переход к шагу 4.

Шаг 4. В выбранную клетку, аналогично предыдущим методам, записывают максимально возможное число единиц продукции, которое разрешается ограничениями на предложение и спрос. После этого вычеркивают либо строку, если предложение поставщика исчерпано, либо столбец, если спрос потребителя удовлетворен.

Если все клетки таблицы заполнены или вычеркнуты, то план перевозок построен. В противном случае переходят к шагу 2 без учета вычеркнутых и заполненных клеток.

В методе Фогеля используются штрафы, взимаемые за неудачей выбор маршрута. Рассчитанные на шаге 2 разности между двумя уровнями затрат на перевозку являются штрафами за неверно выбранный маршрут перевозки.

Пример

Решение.

Разности по строкам будем записывать в правой части табл., разности по столбцам — внизу табл. Максимальную разность будем отмечать кружком. Наименьший тариф в первой строке равен 1. Ближайший к нему равен 3. Разность равна 1. Наименьший тариф во второй строке 4. Ближайшее к нему значение 5. В третьей строке 2 и 3, соответственно. Разности по всем строкам равны 1.

Таблица

 

№	1	2	3	4	Предложение	Разность по столбцам
1	1	8	1 50	2 120	160	1	5	-	-
2	1 120	5 20	9	8	140	1	1	1	1
3	9	2 30	3 140	6	170	1	1	1	7
Спрос	120	50	190	110
Разность по строкам	3	3	3	4
	3	3	3	-
	5	3	6	-
	5	3	-	-

 

В первом столбце наименьший тариф c₂₁= 4. Ближайшее значение с₁₁ = 7, с₁₁ – c₂₁ = 7 – 4 = 3. Во втором столбце наименьшее значение c₃₂ = 3. Ближайшее значение с₂₂ = 5, с₂₂ – c₃₂ = 5 – 2 = 3.

Третий столбец: с₁₃ = 1, с₃₃ = 3 , с₃₃ – с₁₃ = 3 -1 = 3.

Четвертый столбец: с₁₄= 2 , с₃₄ = 6 , с₃₄ – с₁₄ = 6 – 2 = 4 .

Максимальная из всех разностей 4 находится в четвертом столбце.  В этом столбце клетка с наименьшим тарифом с₁₄ = 2 находится в первой строке. В эту клетку помещаем максимально возможное значение: х₁₄ =min(110,160) = 110. Четвертый потребитель полностью удовлетворил свой спрос, и четвертый столбец вычеркиваем.

Повторяем предыдущие действия без учета вычеркнутых и заполненных клеток.

Первая строка: минимальный тариф с₁₃ = 1. Ближайшее значение  с₁₁ =7, с₁₁ – с₁₃ =7-1 = 6.

Вторая строка: минимальный тариф c₂₁= 4. Ближайшее значение  с₂₂ = 5. с₂₂-с₂₁ = 5 – 4 = 1.

Третья строка: с₃₂ = 2, с₃₃ = 3 , с₃₃ – с₃₂ = 3 – 2 = 1.

Первый столбец: минимальный тариф c₂₁ = 4. Ближайшее значение с₁₁ =7,

с₁₁ – c₂₁ =7-4 = 3 .

Второй столбец: с₃₂ = 2, с₂₂ = 5, с₂₂ – с₃₂ = 5 – 2 = 3.

Третий столбец: с₁₃ = 1. с₃₃ ⁼ 3, с₃₃ — с₁₃ =3 -1 = 3.

Максимальная разность равна 6 и стоит в первой строке. Минимальный тариф в первой строке с₁₃ = 1. В эту клетку помещаем х₁₃ = min(160 -110,190) = 50.  

Вычеркиваем первую строку.

Повторяем все действия без учета первой строки и четвертого столбца.

Вторая строка: с₂₁ = 4 , с₂₂ = 5, с₂₂ – c₂₁ = 5 – 4 = 1.

Третья строка: с₃₂ = 2 , с₃₃ = 3 , с₃₃ – с₃₂ = 3 – 2 = 1.

Первый столбец: c₂₁ = 4 , с₃₁ = 9, с₃₁ – c₂₁ = 9 – 4 = 5.

Второй столбец: с₃₂ = 2, с₂₂ = 5, с₂₂ – с₃₂= 5 – 2 = 3.

Третий столбец: с₃₃ = 3 , с₂₃ = 9 , с₂₃ – с₃₃ = 9 – 3 = 6.

Максимальная разность равна 6 и стоит в третьем столбце. Минимальный из оставшихся тарифов в этом столбце с₃₃ = 3, х₃₃ = = min(170, 90 – 50) = 140. Спрос третьего потребителя удовлетворен, третий столбец вычеркиваем.

Вновь составляем разности для невычеркнутых строк и столбцов.

Вторая строка: с₂₁ = 4 , с₂₂ = 5, с₂₂ – с₂₁=5 – 4 = 1.

Третья строка: с₃₂ = 2 , с₃₁ = 9, с₃₁ – с₃₂ = 9 – 2 = 7 .

Первый столбец: c₂₁ = 4 , с₃₁ =9, с₃₁ – c₂₁ = 9 – 4 = 5.

Второй столбец: с₃₂ = 2, с₂₂ = 5, с₂₂ – с₃₂ = 5 – 2 = 3.

Максимальная разность стоит в третьей строке. Минимальный тариф в этой строке с₃₂ = 2, х₃₂ = min(170 -140,50) = 30.

Предложение поставщика исчерпано, и третью строку вычеркиваем.

Осталась одна строка транспортной таблицы. Это вторая строка.  В этой строке сначала заполняем клетку с наименьшим тарифом c₂₁=4, х₃₁ =min(140,120) = 120 . Оставшееся предложение второго поставщика записываем в единственную свободную клетку х₂₂ = min(140 -120,50 –  – 30) = 20.

Полученный по методу Фогеля план перевозок имеет вид

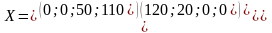
Затраты на перевозку по этому плану составляют

F(x)=*1 + 110*2+120*4+20*5+30*2+140*3=1430д.ед.