11) Конденсаторы.
П
ростейший
конденсатор – система из двух плоских
проводящих пластин, расположенных
параллельно друг другу на малом по
сравнению с размерами пластин расстоянии
и разделенных слоем диэлектрика. Такой
конденсатор называется плоским.
Электрическое поле плоского конденсатора
в основном локализовано между пластинами;
однако, вблизи краев пластин и в окружающем
пространстве также возникает сравнительно
слабое электрическое поле, которое
называют полем рассеяния.
Каждая из заряженных пластин плоского
конденсатора создает вблизи поверхности
электрическое поле, модуль напряженности
которого выражается соотношением
.
Согласно принципу суперпозиции,
напряженность
поля, создаваемого обеими пластинами,
равна сумме напряженностей
и
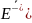полей каждой из пластин:
Внутри конденсатора вектора
и
параллельны; поэтому модуль напряженности
суммарного поля равен
.
Вне пластин вектора
и
направлены в разные стороны, и поэтому
E = 0. Поверхностная плотность σ
заряда пластин равна q / S, где q –
заряд, а S – площадь каждой пластины.
Разность потенциалов Δφ между пластинами
в однородном электрическом поле равна
Ed, где d – расстояние между пластинами.
Из этих соотношений можно получить
формулу для электроемкости плоского
конденсатора:
Таким образом, электроемкость плоского
конденсатора прямо пропорциональна
площади пластин (обкладок) и обратно
пропорциональна расстоянию между ними.
Если пространство между обкладками
заполнено диэлектриком, электроемкость
конденсатора увеличивается в ε раз:
П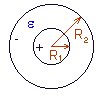
римерами
конденсаторов с другой конфигурацией
обкладок могут служить сферический и
цилиндрический конденсаторы.
С
ферический
конденсатор – это система из двух
концентрических проводящих сфер радиусов
R1 и R2.
Цилиндрический конденсатор – система из двух соосных проводящих цилиндров радиусов R1 и R2 и длины L.
Емкости этих конденсаторов, заполненных диэлектриком с диэлектрической проницаемостью ε.
12) Энергия электрического поля.
Энергия электростатического поля - это энергия системы неподвижных точечных зарядов, энергия уединенного заряженного проводника и энергия заряженного конденсатора.
Энергия заряженного конденсатора равна работе внешних сил, которую необходимо затратить, чтобы зарядить конденсатор.
Процесс зарядки конденсатора можно
представить как последовательный
перенос достаточно малых порций заряда
Δq > 0 с одной обкладки на другую. При
этом одна обкладка постепенно заряжается
положительным зарядом, а другая –
отрицательным. Поскольку каждая порция
переносится в условиях, когда на обкладках
уже имеется некоторый заряд q, а между
ними существует некоторая разность
потенциалов
при переносе каждой порции Δq внешние
силы должны совершить работу
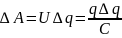
Энергия
конденсатора емкости C, заряженного
зарядом Q, может быть найдена по формуле:
Электрическую энергию Wе следует
рассматривать как потенциальную энергию,
запасенную в заряженном конденсаторе.
Формулы для Wе аналогичны формулам для
потенциальной энергии Eр деформированной
пружины:
,
где k – жесткость пружины, x – деформация,
F = kx – внешняя сила.
По современным представлениям, электрическая энергия конденсатора локализована в пространстве между обкладками конденсатора, то есть в электрическом поле. Поэтому ее называют энергией электрического поля.
Напряженность однородного поля в плоском
конденсаторе равна E = U/d, а его емкость
. Поэтому:
,
где V = Sd – объем пространства между
обкладками, занятый электрическим
полем. Из этого соотношения следует,
что физическая величина
является электрической (потенциальной) энергией единицы объема пространства, в котором создано электрическое поле. Ее называют объемной плотностью электрической энергии.
Энергия поля, созданного любым распределением электрических зарядов в пространстве, может быть найдена путем интегрирования объемной плотности по всему объему, в котором создано электрическое поле.