31) Случаи движения заряженной частицы в магнитном поле.

На заряженную частицу в электростатическом поле действует кулоновская сила, которую можно найти, зная напряженность поля в данной точке: 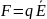. Эта сила сообщает ускорение  

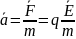
где m — масса заряженной частицы. Как видно, направление ускорения будет совпадать с направлением , если заряд частицы положителен ( ), и будет противоположно , если заряд отрицателен ( ).

Если электростатическое поле однородное ( = const), то ускорение  a = const и частица будет совершать равноускоренное движение (при отсутствии других сил).

Вид траектории частицы зависит от начальных условий. Если вначале заряженная частица покоилась (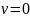 ) или ее начальная скорость сонаправлена с ускорением a, то частица будет совершать равноускоренное прямолинейное движение вдоль поля и ее скорость будет расти. Если 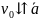, то частица будет тормозиться в этом поле.

Если угол между начальной скоростью и ускорением острый 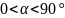(или тупой), то заряженная частица   будет двигаться по параболе.  

Во всех случаях при движении заряженной частицы будет изменяться модуль скорости, а следовательно, и кинетическая энергия частицы.

1.  Заряженная частица влетает в магнитное поле со скоростью , направленной вдоль поля  или противоположно  направлению магнитной индукции поля .

В этих случаях сила Лоренца  и частица будет продолжать двигаться равномерно прямолинейно.

2. Заряженная частица движется перпендикулярно линиям магнитной индукции

тогда сила Лоренца 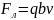 , следовательно, и сообщаемое ускорение будут постоянны по модулю и перпендикулярны к скорости частицы.

В результате частица будет двигаться по окружности , радиус которой можно найти на основании второго закона Ньютона:

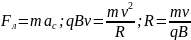
Отношение — называют удельным зарядом частицы.

Период вращения частицы 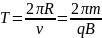то есть период вращения не зависит от скорости частицы и радиуса траектории.

Движение частицы можно представить в виде суперпозиции равномерного прямолинейного движения вдоль поля со скоростью  и движения по окружности с постоянной по модулю скоростью  в плоскости, перпендикулярной полю.

Радиус окружности определяется аналогично предыдущему случаю, только надо 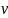заменить  на , то есть 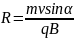. В результате сложения этих движений возникает движение по винтовой линии, ось которой параллельна магнитному полю. Шаг винтовой линии

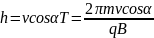
Направление, в котором закручивается спираль, зависит от знака заряда частицы.

3 2) Работа по перемещению проводника с током в магнитном поле.

Н а проводник с током в магнитном поле действуют силы, которые определяются с помощью закона Ампера. Если проводник не закреплен (например, одна из сторон контура сделана в виде подвижной перемычки, рис. 1), то под действием силы Ампера он в магнитном поле будет перемещаться. Значит, магнитное поле совершает работу по перемещению проводника с током. Для вычисления этой работы рассмотрим проводник длиной l с током I (он может свободно двигаться), который помещен в однородное внешнее магнитное поле, которое перпендикулярно плоскости контура. Сила, направление которой определяется по правилу левой руки, а значение — по закону Ампера, рассчитывается по формуле . Под действием данной силы проводник передвинется параллельно самому себе на отрезок dx из положения 1 в положение 2. Работа, которая совершается магнитным полем, равна: , так как 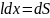— площадь, которую пересекает проводник при его перемещении в магнитном поле, — поток вектора магнитной индукции, который пронизывает эту площадь. Значит, 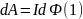, т. е. работа по перемещению проводника с током в магнитном поле равна произведению силы тока на магнитный поток, пересеченный движущимся проводником. Данная формула справедлива и для произвольного направления вектора В. Рассчитаем работу по перемещению замкнутого контура с постоянным током I в магнитном поле. Будем считать, что контур М перемещается в плоскости чертежа и в результате бесконечно малого перемещения перейдет в положение М', изображенное на рис. 2 штриховой линией. Направление тока в контуре (по часовой стрелке) и магнитного поля (перпендикулярно плоскости чертежа — за чертеж или от нас) дано на рисунке. Контур М условно разобьем на два соединенных своими концами проводника: и . 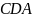Работа dA, которая совершается силами Ампера при исследуемом перемещении контура в магнитном поле, равна алгебраической сумме работ по перемещению проводников AВС (dA₁) и CDA (dA₂), т. е. 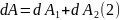. Силы, которые приложенны к участку контура, образуют острые углы с направлением перемещения, поэтому совершаемая ими работа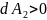 . Используя (1), находим, эта работа равна произведению силы тока в нашем контуре на пересеченный проводником магнитный поток. Проводник пересекает при своем движении поток dФ₀ сквозь поверхность, выполненную в цвете, и поток 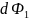, который пронизывает контур в его конечном положении. Значит, Силы, которые действуют на участок AВС контура, образуют тупые углы с направлением перемещения, значит совершаемая ими работа dA₁<0. Проводник AВС пересекает при своем движении поток dФ₀ сквозь поверхность, выполненную в цвете, и поток dФ1, который пронизывает контур в начальном положении. Значит, 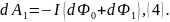Подставляя (3) и (4) в (2), найдем выражение для элементарной работы: где — изменение магнитного потока сквозь площадь, которая ограничена контуром с током. Таким образом, . Проинтегрировав выражение , найдем работу, которая совершается силами Ампера, при конечном произвольном перемещении контура в магнитном поле: , значит, работа по перемещению замкнутого контура с током в магнитном поле равна произведению силы тока в контуре на изменение магнитного потока, сцепленного с контуром. Выражение верно для контура любой формы в произвольном магнитном поле.