1. Минералы - кристаллические элементные или химические соединения, возникающие в ходе геологических процессов (ММА-1995 – Комиссия по новым минералам и названиям минералов).

2. Минеральный вид. К одному минеральному виду относятся все минеральные индивиды, характеризующиеся:

- одинаковой структурной группой

- химическим составом, непрерывно изменяющимся в определенных пределах

- равновесным существованием в определенных термодинамических условиях земной коры.

Минеральные разновидности: структурные, химические

3. Кристаллические твердые вещества характеризуются трехмерным закономерным периодическим размещением их химических строительных частиц (атомов, ионов, комплексов, молекул)

Для кристаллического вещества характерны:

- симметрия внутренней структуры

- симметрия внешней формы

- симметрия физических свойств

- симметрия взаимодействии кристалла и среды

4. 1-го рода «связывают» друг с другом конгруэнтно равные фигуры (совмещаются при наложении или вложении) - правый-правый, левый-левый

Поворот вокруг оси n-ого порядка –

поворотная ось Ln n = 1, 2, 3, 4, 6.

Порядок оси = 360/a a - элементарный угол поворота

Оси симметрии могут быть: а) полярные – на концах оси разные элементы фигуры; б) неполярные (биполярные) – на концах оси одинаковые элементы фигуры

Элементы симметрии 2-го рода «связывают» зеркально равные - энантиоморфные фигуры - правый-левый = зеркальные плоскости, центр симметрии + зеркальные и инверсионные оси.

Отражение в плоскости –

плоскость симметрии Р

Отражение в точке (инверсия) –

центр симметрии, инверсии С

Поворот с отражением в точке - инверсионная ось Lni - с черточкой наверху. Порядок оси - 1, 2, 3, 4, 6.

5. Оси симметрии могут быть: а) полярные – на концах оси разные элементы фигуры; б) неполярные (биполярные) – на концах оси одинаковые элементы фигуры

Инверсионные сложные оси могут быть представлены:

L6 = L3+ ┴P.

L4 – является оригинальной или незаменимой простыми элементами.

L3 = L3 + C.

L2 = P.

L1= C.

7. плоскость симметрии Р –максимум - 9

центр симметрии С – каждой грани есть обратно параллельная

L2 - может быть в фигуре - 1, 3, 4, 6; 2 (с инв. L4) – ось низшего порядка.

L3 - может быть 1 или 4.

L4 - может быть 1 или 3 (в т.ч. инверсионные).

L6 - может быть одна.

оси высшего порядка.

Порядок оси = симметрии грани или количеству граней в вершине

Формула симметрии состоит из записанных подряд элементов симметрии данного кристалла в определенной последовательности: оси высшего порядка  оси L2  плоскости симметрии  центр симметрии. В кубической сингонии на втором месте всегда стоит 4L3. Если какой-либо элемент отсутствует, он опускается.

8. 1. Осевая теорема Эйлера - Равнодействующей двух пересекающихся осей симметрии является третья ось, проходящая через точку их пересечения.

Частные случаи:

1) если есть поворотная ось симметрии порядка n и перпендикулярно этой оси проходит поворотная ось 2-го порядка, то всего имеется n осей 2-го порядка;

2) если под углом a пресекаются две поворотные оси 2-го порядка, то перпендикулярно им проходит поворотная ось с элементарным углом поворота в 2 раза большим угла пересечения (2a).

2. Точка пересечения оси симметрии второго порядка (L2) или четной оси симметрии с перпендикулярной ей плоскостью симметрии есть центр симметрии. Обратная теорема: Если есть центр симметрии и через него проходит плоскость симметрии, то перпендикулярно этой плоскости через центр симметрии проходит двойная ось симметрии.

3. Линия пересечения двух плоскостей симметрии является осью симметрии, причем, угол поворота вокруг оси вдвое больше угла между плоскостями. Следствия: 1) в присутствии оси симметрии порядка n и плоскости, проходящей вдоль оси, всего имеем n таких плоскостей;

2) Плоскость, проходящая вдоль инверсионной оси симметрии 3-его и 4-го порядков, приводит к появлению оси 2-го порядка, перпендикулярной инверсионной оси и проходящей по биссектрисе угла между плоскостями.

9. Принцип вывода классов симметрии

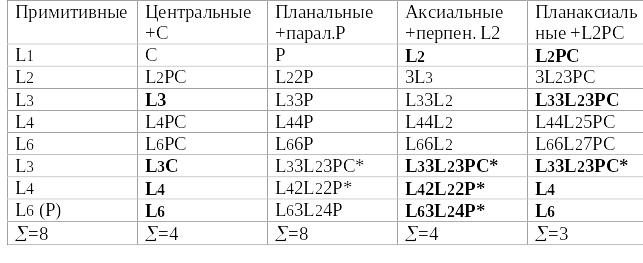
Точечная группа симметрии = класс симметрии = вид симметрии = полная совокупность элементов симметрии фигуры (многогранника).

32 класса симметрии подразделяются на 3 категории (низшую, среднюю и высшую ) и 7 (6) сингоний

10. В сингонию (сходноугольность) объединяются те кристаллы, для которых одинакова симметрия элементарных ячеек их структур и одинакова система координат. В сингониях одинаковое количество единичных направлений: в низших – не менее 3-х, в средних – одно, в высшей – нет.

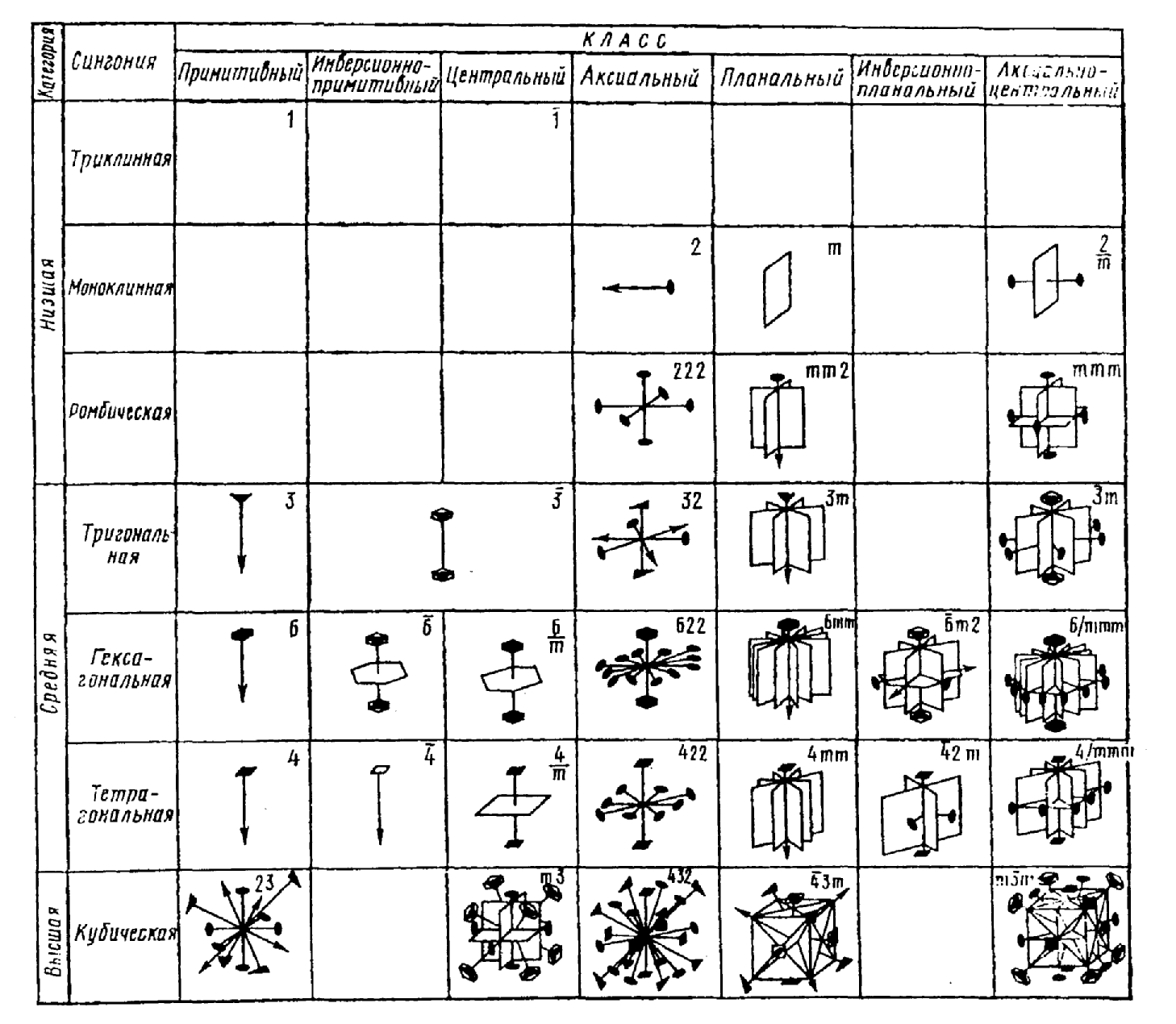
11. Международная символика (символы Германа-Могена) элементов симметрии кристаллических многогранников и классов симметрии:

Плоскость симметрии – m.

Центр симметрии (инверсии) – 1(с черточкой наверху).

Поворотные оси - 1, 2, 3, 4, 6.

Инверсионные оси - 3, 4, 6 (с черточкой).

nm - ось симметрии n -порядка и n плоскостей вдоль нее.

n/m ось симметрии n-порядка и перпендикулярная ей плоскость симметрии.

n2 - ось симметрии n порядка и n осей 2-го порядка, ей перпендикулярных.

n/mm - ось n-го порядка и плоскости: одна перпендикулярная и n параллельных ей.

Знак «/» показывает, что элементы симметрии расположены взаимно перпендикулярно. Обозначаются только важнейшие, «порождающие» элементы симметрии, предпочтение отдается плоскости симметрии

12. Простая форма - семейство граней, взаимосвязанных симметрическими операциями данного класса симметрии

Простые формы могут быть:

По возможности ограничивать пространство:

открытые и закрытые

По расположению относительно элементов симметрии:

общие и частные

В любом выпуклом многограннике число вершин (в), граней (г) и ребер (р) подчиняется формуле Эйлера (Эйлера-Декарта): в+г=р+2.

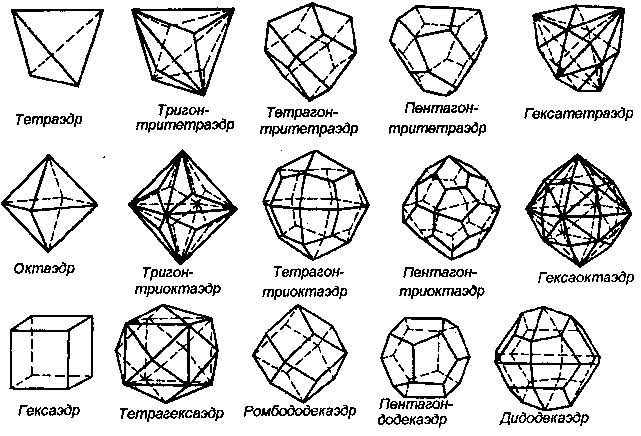
14. Число простых форм конечно (47), т.к. конечно число групп симметрии, число различных положений граней в каждой группе.

Простые формы кубической сингонии

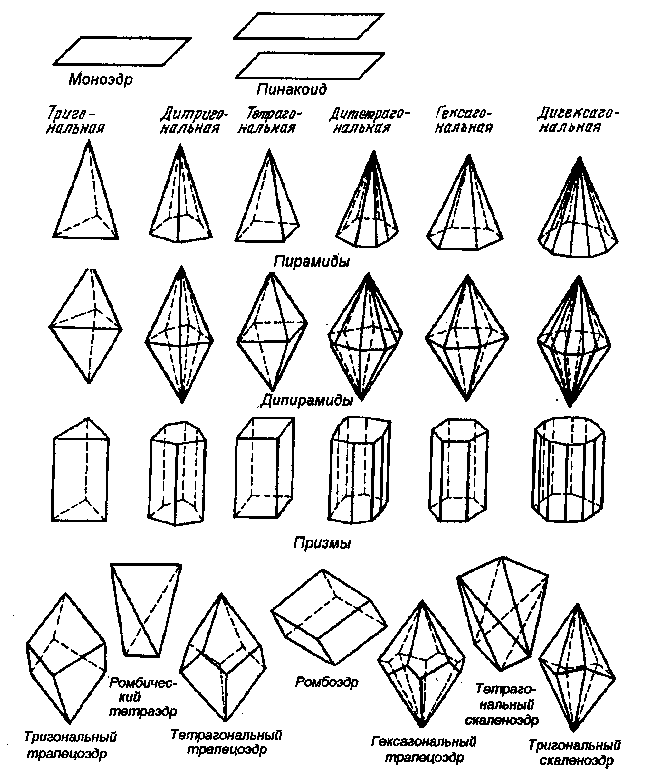
Простые формы низших сингоний

моноэдр пинакоид диэдр

ромб. призма ромб. тетраэдр ромб. пирамида ромб. дипирамида

Простые формы средних сингоний

15. Кристаллографические координатные оси

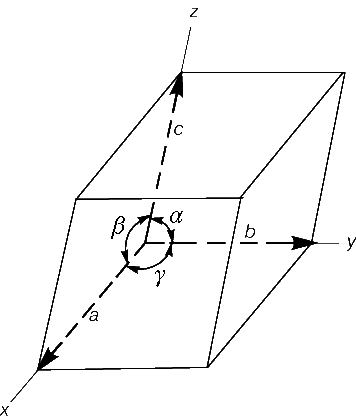
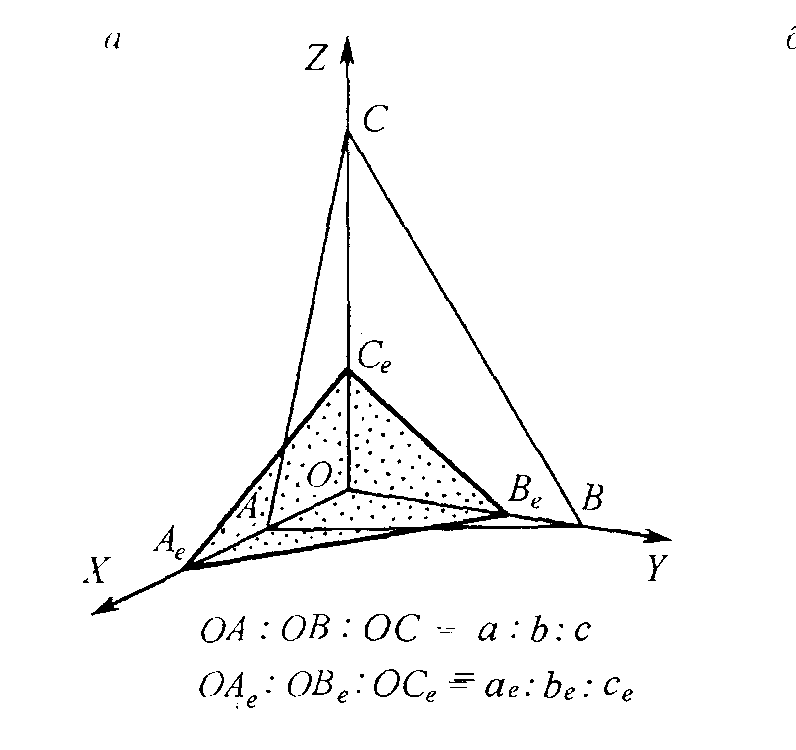
Для гексагональной и тригональной сингонии вводится дополнительная ось U, составляющая с осью а и b угол 120^о и направленная в противоположную сторону положительным концом.

16 Для описания положения в пространстве грани используются символы граней или индексы Миллера. Для того чтобы их получить, надо правильно установить кристалл. Установка кристалла - это правила выбора координатных осей и единичной грани (параметрической грани) в кристалле. Начало координат – центр кристалла. Параметрическая грань служит единицей измерений других граней; у нее абсолютные величины параметров ao, bo, co могут быть различными, но относительные равны 1. Правила установки кристаллов и выбора единичной грани приведены в таблице 3.

Правила установки кристаллов и выбора единичной грани

17. Начало координат – центр кристалла.

a/ao : b/bo : c/co - эти параметры обозначаются

как p : q : r – параметры Вейсса

1/p : 1/q : 1/r или ao/a : bo/b : co/c -

(h k l) Индексы Миллера

Для гексагональной и тригональной сингонии вводится дополнительная ось U, составляющая с осью а и b угол 120 и направленная в противоположную сторону положительным концом.

Миллеровские индексы у кристаллов этих сингоний имеют вид: (h k i l)

18. Закон Гаюи

Отношения отрезков, отсекаемых двумя гранями кристалла на координатных осях (или на трех пересекающихся ребрах) относятся друг к другу как целые, взаимно простые и малые числа.

Второй вариант формулировки: Отношение отрезков (параметров), отсекаемых гранью кристалла на 3-х координатных осях равно отношению целых и взаимно простых чисел при условии, что параметры измерены особыми единицами для каждой из осей. За единицы измерения должны быть взяты параметры некоторой другой грани кристалла - единичной грани (она пересекает все оси в положительной части).

19. Закон постоянства углов (Стено, 1669) 1-й закон кристаллографии «При одних и тех же условиях кристаллы одного вида заключают между соответствующими гранями одинаковые углы»,

20. Кристаллическая решетка - схема внутреннего строения кристаллического вещества. Для построения пространственной решетки нужно 4 исходных точки, далее идет параллельный перенос (плоские сетки определяются тремя точками).

Причина геометрической правильности форм кристалла в закономерном внутреннем строении. Периодичность кристалла выражается в том, что одинаковые структурные элементы закономерно повторяются, эта повторяемость может быть описана при помощи трансляций - переноса структуры из точки в точку на расстояние, равное периоду трансляции (периоду идентичности). Кристалл можно рассматривать как пространственную решетку - бесконечное трехмерное периодическое образование. Кристаллическая решетка - схема внутреннего строения кристаллического вещества. Для построения пространственной решетки нужно взять 4 исходных точки, далее идет параллельный перенос по трем направлениям. Основных троек трансляций всего 14, они называются решетками Бравэ или группами трансляций.

21. Решетки Бравэ

Совокупность всех трансляций в кристаллической структуре составляет трансляционную группу или группу переносов = кристаллическую решетку Бравэ.

Узел решетки может быть, а может и не быть материальной частицей, но он связан с ней. Количество материальных частиц в ячейке равно или больше количества узлов. Узлы в решетке идентичны.

Параметры решеток Бравэ каждой сингонии полностью совпадают с данными по установке кристаллов соответствующей сингонии

Правила обозначения решеток Бравэ:

P – примитивная

C (А, В) – базоцентрированная

I – объемоцентрированная

F – гранецентрированная

R - ромбоэдрическая),

Правила выбора элементарной ячейки в решетках

– по мере убывания значимости:

1. Ячейка должна наилучшим образом отражать симметрию сетки и соответствовать максимальной симметрии соответствующей сингонии. Ребра элементарной ячейки должны быть трансляциями решетки.

2. По возможности должна иметь максимальное количество прямых углов или равных углов и равных ребер.

3. Обладала бы наименьшим объемом.

Размеры решеток - это есть размеры их элементарных ячеек.

23. Сочетания элементов симметричности дают 230 пространственных (Федоровских) групп симметрии

Пространственной группой симметрии называется совокупность всех возможных элементов симметрии кристаллической структуры.

Обозначения групп симметрии:

1. Тип решетки Бравэ

1. Если в одном направлении есть плоскости скользящего и зеркального отражения, то вводится простая плоскость.

3. Если в одном направлении есть и плоскости и оси, то в символе указывается плоскость.

4. Если на какой-то позиции нет элемента, то пишутцифру «1».

5. Перпендикулярность элементов обозначается «/».

6. Порядок расположения символов при обозначении пространственных групп аналогичен системе, которая использовалась для обозначения точечных групп.