
- •1.Понятие функции одной переменной
- •10. Сравнение бесконечно малых функций.
- •Следствия из первого замечательного предела
- •Правила нахождения производных
- •15. Таблица основных производных
- •16.Производные высших порядков
- •17. Определение дифференциала функции
- •18. Дифференциалы высших порядков
- •Примеры решения задач
- •Решение.
- •3. Частные производные.
- •4. Геометрическая интерпретация частных
15. Таблица основных производных
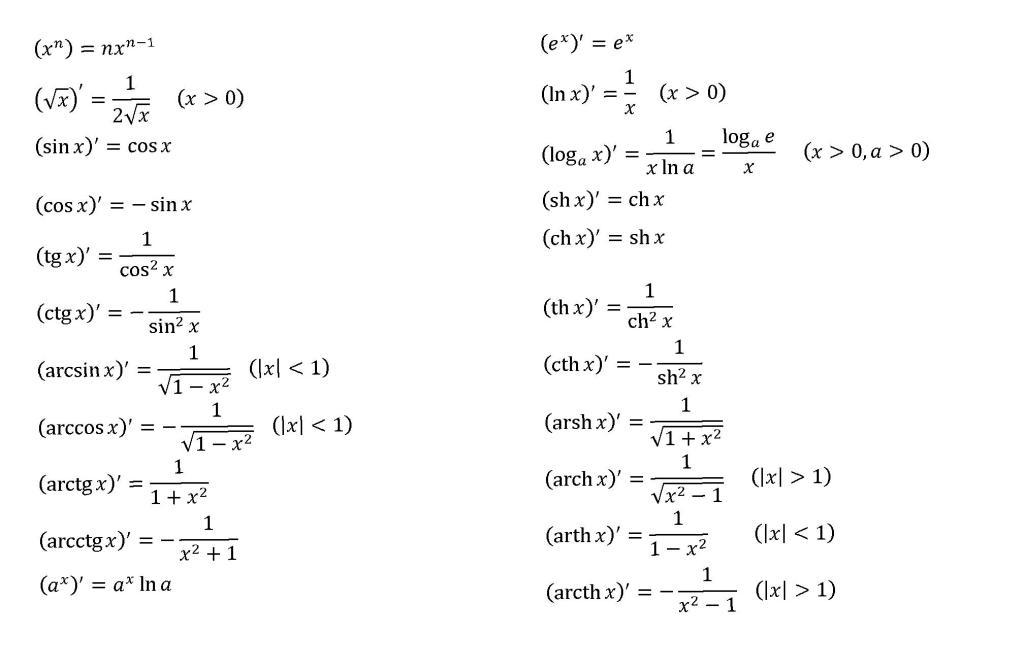
16.Производные высших порядков
Ясно, что производная

функции y =f (x) есть также функция от x:
y' =f ' (x)
. Если функция f ' (x) дифференцируема, то её производная обозначается символомy'' =f '' (x) и называется второй производной функции f(x) или производной функции f(x) второго порядка. Пользуясь обозначением
![]()
можем написать
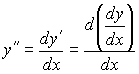
Пример.
Очень удобно пользоваться также обозначением
![]() ,
,
указывающим, что функция y=f(x) была продифференцирована по x два раза. Производная второй производной, т.е. функции y''=f '' (x) , называется третьей производной функции y=f(x) или производной функции f(x) третьего порядка и обозначается символами
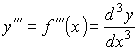 .
.
Вообще n-я производная или производная n-го порядка функции y=f(x)обозначается символами
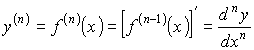
17. Определение дифференциала функции
Дифференциалом
функции называется
линейная относительно ![]() часть
приращения функции. Она обозначается
как
часть
приращения функции. Она обозначается
как ![]() или
или ![]() .
Таким образом:
.
Таким образом:
![]()
18. Дифференциалы высших порядков
Дифференциалом ![]() -го
порядка
-го
порядка ![]() функции
функции ![]() называется
дифференциал от дифференциала
называется
дифференциал от дифференциала ![]() -го
порядка этой функции, то есть
-го
порядка этой функции, то есть
![]()
19)Теорема
Лопита́ля
(также правило
Бернулли — Лопиталя[1]) —
метод нахождения пределов
функций,
раскрывающий
неопределённости
вида
![]() и
и
![]() .
Обосновывающая метод теорема утверждает,
что при некоторых условиях предел
отношения функций
равен пределу отношения их производных.
.
Обосновывающая метод теорема утверждает,
что при некоторых условиях предел
отношения функций
равен пределу отношения их производных.
Теорема Лопиталя:
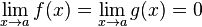 либо
либо
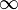 ;
;
 и
и
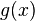 дифференцируемы
в проколотой окрестности
дифференцируемы
в проколотой окрестности
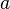 ;
;
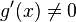 в
проколотой окрестности
;
в
проколотой окрестности
;
существует
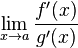 ,
,
тогда
существует
![]() .
.
Пределы также могут быть односторонними.
Отношение бесконечно малых
Докажем
теорему для случая, когда пределы функций
равны нулю (то есть неопределённость
вида
![]() ).
).
Поскольку
мы рассматриваем функции
![]() и
и
![]() только
в правой проколотой полуокрестности
точки
,
мы можем непрерывным
образом
их доопределить в этой точке: пусть
только
в правой проколотой полуокрестности
точки
,
мы можем непрерывным
образом
их доопределить в этой точке: пусть
![]() .
Возьмём некоторый
.
Возьмём некоторый
![]() из
рассматриваемой полуокрестности и
применим к отрезку
из
рассматриваемой полуокрестности и
применим к отрезку
![]() теорему
Коши.
По этой теореме получим:
теорему
Коши.
По этой теореме получим:
![]() ,
,
но
,
поэтому
![]() .
.
Дальше,
записав определение предела
отношения производных
и обозначив последний через
![]() ,
из полученного равенства выводим:
,
из полученного равенства выводим:
 для
конечного предела и
для
конечного предела и
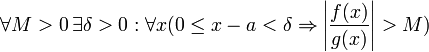 для
бесконечного,
для
бесконечного,
что является определением предела отношения функций.
Отношение бесконечно больших
Докажем
теорему для неопределённостей вида
![]() .
.
Пусть,
для начала, предел отношения производных
конечен и равен
.
Тогда, при стремлении
к
справа,
это отношение можно записать как
![]() ,
где
,
где
![]() —
O(1).
Запишем это условие:
—
O(1).
Запишем это условие:
![]() .
.
Зафиксируем
![]() из
отрезка
из
отрезка
![]() и
применим теорему
Коши
ко всем
из
отрезка
и
применим теорему
Коши
ко всем
из
отрезка
![]() :
:
![]() ,
что можно привести к следующему виду:
,
что можно привести к следующему виду:
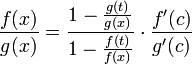 .
.
Для
,
достаточно близких к
,
выражение имеет смысл; предел первого
множителя правой части равен единице
(так как
![]() и
и
![]() —
константы,
а
—
константы,
а
![]() и
стремятся
к бесконечности). Значит, этот множитель
равен
и
стремятся
к бесконечности). Значит, этот множитель
равен
![]() ,
где
,
где
![]() —
бесконечно малая функция при стремлении
к
справа.
Выпишем определение этого факта,
используя то же значение
—
бесконечно малая функция при стремлении
к
справа.
Выпишем определение этого факта,
используя то же значение
![]() ,
что и в определении для
:
,
что и в определении для
:
![]() .
.
Получили,
что отношение функций представимо в
виде
![]() ,
и
,
и
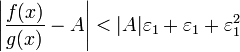 .
По любому данному
можно
найти такое
.
По любому данному
можно
найти такое
![]() ,
чтобы модуль разности отношения функций
и
был
меньше
,
значит, предел отношения функций
действительно равен
.
,
чтобы модуль разности отношения функций
и
был
меньше
,
значит, предел отношения функций
действительно равен
.
Если же предел бесконечен (допустим, он равен плюс бесконечности), то
![]() .
.
В
определении
будем
брать
![]() ;
первый множитель правой части будет
больше 1/2 при
,
достаточно близких к
,
а тогда
;
первый множитель правой части будет
больше 1/2 при
,
достаточно близких к
,
а тогда
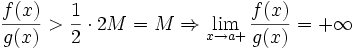 .
.
Для других баз доказательства аналогичны приведённым.
Примеры
![]()
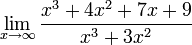 Здесь
можно применить правило Лопиталя 3
раза, а можно поступить иначе. Нужно
разделить и числитель, и знаменатель
на x в наибольшей степени(в нашем случае
Здесь
можно применить правило Лопиталя 3
раза, а можно поступить иначе. Нужно
разделить и числитель, и знаменатель
на x в наибольшей степени(в нашем случае
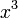 ).
В этом примере получается:
).
В этом примере получается:
![]()
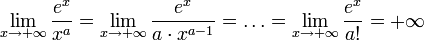 ;
;
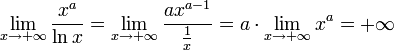 при
при
 .
.
20)Говорят,
что функция
![]() имеет
максимум
в точке
имеет
максимум
в точке
![]() ,
т.е. при
,
т.е. при
![]() ,
если
,
если
![]() для
всех точек
для
всех точек
![]() ,
достаточно близких к точке
,
достаточно близких к точке
![]() и
отличных от неё.
и
отличных от неё.
Говорят,
что функция
имеет
минимум
в точке
,
т.е. при
,
если
![]() для
всех точек
,
достаточно близких к точке
и
отличных от неё.
для
всех точек
,
достаточно близких к точке
и
отличных от неё.
Максимум и минимум функции называются экстремумами функции.
Теорема
(необходимое условие экстремума функции
двух переменных). Если функция
достигает
экстремума при
,
то каждая частная производная первого
порядка от
![]() или
обращается в нуль при этих значениях
аргументов, или не существует.
или
обращается в нуль при этих значениях
аргументов, или не существует.
Теорема
(достаточное условие экстремума функции
двух переменных). Пусть в некоторой
области, содержащей точку
функция
имеет
непрерывные частные производные до
третьего порядка включительно. Пусть,
кроме того, точка
является
критической точкой функции
![]() ,
т.е.
,
т.е.
 ,
тогда
при
:
1)
имеет
максимум, если дискриминант
,
тогда
при
:
1)
имеет
максимум, если дискриминант
![]() и
и
![]() ,
где
,
где
 ;
2)
имеет
минимум, если дискриминант
и
;
2)
имеет
минимум, если дискриминант
и
![]() ;
3)
не
имеет ни минимума, ни максимума, если
дискриминант
;
3)
не
имеет ни минимума, ни максимума, если
дискриминант
![]() ;
4)
если
;
4)
если
![]() ,
то экстремум может быть, а может и не
быть (требуется дополнительное
исследование).
,
то экстремум может быть, а может и не
быть (требуется дополнительное
исследование).
