1.Понятие функции одной переменной

Рассмотрим два числовых множества X и Y. Правило f, по которому каждому числу хI Х ставится в соответствие единственное число yI Y, называется числовой функцией, заданной на множестве Х и принимающей значения во множестве Y. Таким образом, задать функцию, значит задать три объекта: 1) множество Х (область определения функции); 2) множество Y (область значений функции); 3) правило соответствия f (сама функция). Например, поставим в соответствие каждому числу его куб. Математически это можно записать формулой y=x3. В этом случае правило f есть возведение числа х в третью степень. В общем случае, если каждому х по правилу f соответствует единственный y, пишут y = f(x). Здесь "х" называют независимой переменной или аргументом, а "y" -зависимой переменной (т.к. выражение типа x3 само по себе не имеет определенного числового значения пока не указано значение х) или функцией от х. О величинах х и y говорят, что они связаны функциональной зависимостью. Зная все значения х и правило f можно найти все значения у. Например, если х=2, то функция f(x) =x3 принимает значение у= f(2) =23 =8.

Совокупность всех тех значений, которые принимает аргумент х функции y = f (x), называется областью определения этой функции. Совокупность всех тех значений, которые принимает сама функция у, называется областью изменения этой функции.

2. Основные свойства функций: четность, нечетность, периодичность, монотонность, ограниченность Периодичность Определение. Функция f называется периодичной, если существует такое число , что f(x+

)=f(x), для всех x D(f). Естественно, что таких чисел существует бесчисленное множество. Наименьшее положительное число Т называется периодом функции. Четность Определение. Функция f называется четной, если для всех х из D(f) выполняется свойство f(-х) = f(х). Если f(-х) = -f(х), то функция называется нечетной. Если ни одно из указанных соотношений не выполняется, то функция называется функцией общего вида. Монотонность Определение. Функция f: X —> R называется возрастающей (убывающей), если для любых выполняется условие:

);

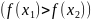
Определение. Функция Х —>R называется монотонной на X, если она на X возрастающая или убывающая. Если f монотонна на некоторых подмножествах из X, то она называется кусочно-монотонной.

Определение. Функция называется ограниченной, если ограничена ее область значений.

5. Обратные тригонометрические функции Обра́тные тригонометри́ческие фу́нкции— математические функции, являющиеся обратными к тригонометрическим функциям. К обратным тригонометрическим функциям обычно относят 4 функций: аркси́нус ,аркко́синус ,аркта́нгенс, арккота́нгенс

6. Преде́л фу́нкции — одно из основных понятий математического анализа. Функция f(x) имеет предел A в точке x0, если для всех значений x, достаточно близких к x0, значение f(x) близко к A. Основные правила нахождения пределов Предел постоянной величины равен постоянной величине: Предел суммы равен сумме пределов: Предел разности равен разности пределов: Предел функции в степени: Предел корня из функции: 7. БЕСКОНЕЧНО МАЛЫЕ И ИХ СВОЙСТВА Функция α(х) называется бесконечно малой при , если ,т. е. для любого числа ε > 0 существует такое число δ > 0, что для всех х, удовлетворяющих неравенству ,выполняется неравенство . Свойства бесконечно малых. 1. Если функции и являются бесконечно малыми, то функція также есть бесконечно малая. Это свойство распространяется на случай алгебраической суммы любого конечного числа бесконечно малых. 2. Произведение ограниченной при функции на бесконечно малую есть функция бесконечно малая. 3. Произведение постоянной на бесконечно малую есть бесконечно малая. 4. Произведение двух бесконечно малых есть бесконечно малая. Это свойство распространяется на любое конечное число бесконечно малых. 8.Бесконечно большие функции Определение. Функция называется бесконечно большой при ,если . 9. СООТНОШЕНИЕ МЕЖДУ БЕСКОНЕЧНО МАЛЫМИ И БЕСКОНЕЧНО БОЛЬШИМИ ФУНКЦИЯМИ Теорема 1. Если функция f(x) является бесконечно большой при x→a, то функция 1/f(x) является бесконечно малой при x→a. Доказательство. Возьмем произвольное число ε>0 и покажем, что при некотором δ>0 (зависящим от ε) при всех x, для которых |x – a|<δ, выполняется неравенство , а это и будет означать, что 1/f(x) – бесконечно малая функция. Действительно, так как f(x) – бесконечно большая функция при x→a, то найдется δ>0 такое, что как только |x – a|<δ, так |f(x)|>1/ ε. Но тогда для тех же х Теорема 2. Если функция f(x) - бесконечно малая при x→a (или x→∞) и не обращается в нуль, то y=1/f(x) является бесконечно большой функцией.