20. Нормальный(гауссовский) з-н распределения случайных сигналов. Эффект нормализации случайных процессов в узкополосных цепях.

В РТ большое значение и распространение имеют сигналы, являющиеся рез. Совместного действия случайных явлений. Всилу справедливости центральной теоремы теории вероятности такие сигналы описыаются нормальным законом распределения

График нормального з-на рапредления хар-ется след свойствами:

1)кривая графика норм з-на симметрична относительно оси, проходящей через т. m_x

2)Ветви кривой р(х) асимптотически приближаются к оси х при х->∞ и х->-∞

3) При изменении m_x и δ= const кривая з-на рспределения смещаетя вдоль оси х: вправо при увелич m_x,

И влево влево при уменьшении.

4)При измени m_x и δ = const кривая з-на распределения изменяет свой вид:становится более ширкой и низкой при уменьшении δ, более узкой и высокой и при уменьшении δ

Ф-ция распределения

Для вычисления полученного итеграла воспользуемся таблицами спец ф-ции, называемой интеграллм вероятностей и равной

Свойства

Тогда

Пользуясь полученным результатами определим вер-сть того что знач СВ, нах-ся в интревале [a;b]

Воспользуясь получ формулой и опреелим вер-сть попадания Св в норм законом распределения в интервал

Таким образом для СВ с норм з-ном рапсределения выполнение нер-ва

Эффект нормализации Пусть на входе линейной цепи действует случайный стационарный процесс с распределением, отличным от нормального. Если полоса частот его энергетического спектра больше полосы пропускания цепи, то распределение случайного процесса на выходе приближается к нормальному. Чем уже полоса пропускания цепи, тем эффект нормализации проявляется сильнее. Проиллюстрируем эффект нормализации на примере воздействия случайным образом расположенных на оси времени коротких импульсов на высокодобротный контур. Постоянная времени контура велика по сравнению со средней величиной интервалов между импульсами. В момент прихода каждого импульса на контуре возникают медленно затухающие колебания (рис.1).

Н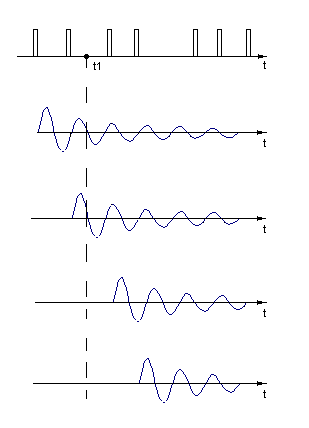 апряжение на контуре в любой момент времени t₁ является суммой свободных колебаний, вызванных предыдущими импульсами и не успевших полностью затухнуть к рассматриваемому моменту времени. Чем уже полоса пропускания, тем длительнее свободные колебания, и, следовательно, тем больше число соизмеримых по величине и несвязанных между собой слагаемых принимает участие в образовании результирующего напряжения в момент t₁.В соответствии с центральной предельной теоремой эти предпосылки достаточны для приближения распределения к нормальному.При спектральном подходе эффект нормализации объясняется тем, что спектр колебания в контуре является суммой спектров отдельных импульсов входной последовательности. Внутри каждого из этих парциальных спектров фазы спектральных составляющих коррелированны, а между фазами корреляции нет из-за случайной расстановки импульсов на оси времени. Чем уже полоса пропускания контура, тем меньшую роль играет корреляция фаз в парциальных спектрах.